Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.
Bài 43 trang 210 SGK
Phần thực của z = 2i là
(A) 2; (B) 2i;
(C) 0; (D) 1.
Lời giải:
Ta có z = 0 + 2i có phần thực là 0.
Chọn (C).
Bài 44 trang 210 SGK
Phần ảo của z = −2i là:
(A) - 2; (B) - 2i;
(C) 0; (D) - 1.
Lời giải:
Ta có z = −2i = 0 − 2i có phần ảo là −2.
Chọn (A).
Bài 45 trang 210 SGK
Số ![]() là
là
(A) số thực; (B) số ảo;
(C) 0; (D) 2.
Lời giải:
Chọn (A).
Bài 46 trang 210 SGK
Số là
(A) số thực; (B) số ảo;
(C) 0; (D) 2i.
Lời giải:
Chọn (B).
Bài 47 trang 210 SGK
Số 1/(1+i) bằng
(A) 1+i; (B) 1/2(1−i);
(C) 1–i; (D) i.
Lời giải:
Chọn (B).
Bài 48 trang 210 SGK
Tập hợp các nghiệm của phương trình z = z/(z+i) là:
(A) {0; 1 − i}; (B) {0};
(C) {1 − i}; (D) {0; 1}.
Lời giải:
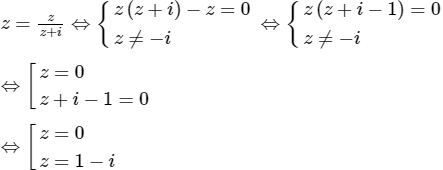
Chọn (A).
Bài 49 trang 210 SGK
Modun của 1 – 2i bằng
(A) 3; (B) √5;
(C) 2; (D) 1.
Lời giải:
z =1−2i thì |z| =√[12 + (−2)2] = √5
Chọn (B).
Bài 50 trang 210 SGK
Modun của −2iz bằng
(A) −2|z|; (B) √2z;
(C) 2|z|; (D) 2.
Lời giải:
|−2iz| = |−2i|.|z| = 2|z|
Chọn (C).
Bài 51 trang 210 SGK
Acgumen của −1 + i bằng
(A) 3π/4 + k2π (k ∈ Z);
(B) −π/4 + k2π (k ∈ Z);
(C) π/4 + k2π (k ∈ Z);
(D) π/2 + k2π ( k ∈ Z).
Lời giải:
Acgumen của −1 + i bằng 3π/4 + k2π (k ∈ Z)
Chọn (A).
Bài 52 trang 210 SGK
Nếu acgumen của z bằng −π/2 + k2π thì
(A) Phần ảo của z là số dương và phần thực của z bằng 0;
(B) Phần ảo của z là số âm và phần thực của z bằng 0;
(C) Phần thực của z là số âm và phần ảo của z bằng 0;
(D) Phần thực và phần ảo của z đều là số âm.
Lời giải:
Do đó phần thực bằng 0, phần ảo âm.
Chọn (B).
Bài 53 trang 211 SGK
Nếu z = cosφ − isinφ thì acgumen của z bằng:
(A) φ + k2π (k ∈ Z);
(B) −φ + k2π (k ∈ Z);
(C) φ + π + k2π (k ∈ Z);
(D) φ + π2 + k2π (k ∈ Z).
Lời giải:
z = cosφ − isinφ = cos(−φ) + isin(−φ)
Vậy z có argumen bằng −φ + k2π (k ∈ Z)
Chọn (B).
Bài 54 trang 211 SGK
Nếu z = −sinφ − icosφ thì acgumen của z bằng:
(A) −π/2 + φ + k2π (k ∈ Z);
(B) −π/2 − φ + k2π (k ∈ Z);
(C) π/2 + φ + k2π (k ∈ Z);
(D) π − φ + k2π (k ∈ Z).
Lời giải:
Ta có:
Argumen của z bằng 3π/2− φ + k2π = −π/2 − φ + (k + 1)2π = −π/2 − φ + 2lπ, l ∈ Z
Chọn (B).


































