Bài 11 trang 16 và 17 SGK
Tìm cực trị của các hàm số sau:
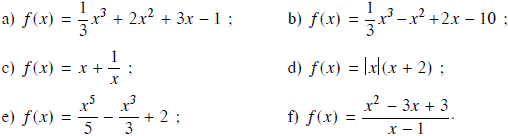
Lời giải:
a) Hàm số đã cho xác định trên R.
Ta có: f’(x) = x2 + 4x +3
Từ đó f’(x) = 0 ⇔ x = -1 hoặc x = -3
Cách 1.
Bảng biến thiên
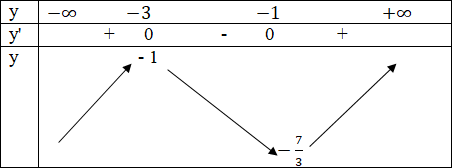
Vậy hàm số đạt cực đại tại điểm x = -3, giá trị cực đại của hàm số là: fCĐ = f(-3) = -1.
Hàm số đạt cực tiểu tại điểm x = -1, giá trị cực tiển của hàm số là fCT = f(-1) = -7/3
Cách 2. f’’(x) = 2x + 4 ⇒ f’’(-3) = -2 < 0; f’’(-1) = 2 > 0
Vậy hàm đạt cực đại tại điểm x = -3 giá trị cực đại của hàm số là:
fCĐ = f(-3) = -1.
Hàm số đạt cực tiểu tại điểm x = -1, fCT = f(-1) = -7/3
b) Tập xác định: R
f'(x) = x2 – 2x + 2 = (x – 1)2 + 1 > 0, ∀x ∈ R => f(x) luôn đồng biến nên hàm số không có cực trị.
c) Tập xác định: R \ {0}
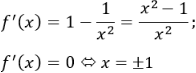
Cách 1.
Bảng biến thiên:
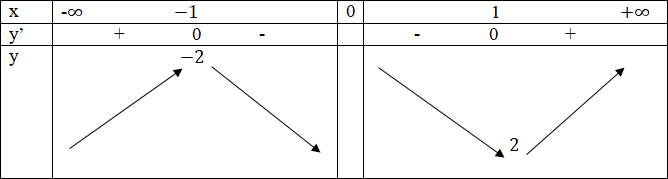
Vậy hàm số cực đại tại x = -1; fCĐ = f(-1 )= -2
Hàm số cực tiểu tại x = 1; fCT = f(1) = 2
Cách 2. ![]()
Vì f’’(- 1) = -2 < 0 nên hàm số đạt cực đại tại x = -1; fCĐ = f(-1) = -2
f''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1; fCT = f(1) = 2
d) f(x) xác định liên tục trên R.
Ta có: 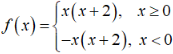
Với x > 0, f'(x) = 2x + 2
Từ đó f'(x) = 0 ⇔ x = -1 (loại)
Với x < 0, f'(x) = -2x – 2
Từ đó f'(x) = 0 ⇔ x = -1 (thỏa mãn)
Với x = 0, hàm số không có đạo hàm (chú ý sgk giải tích 12 nâng cao trang 12)
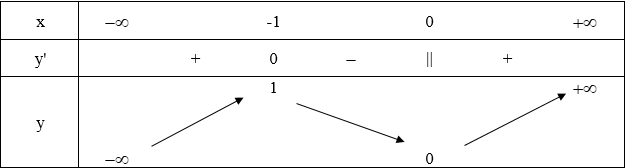
Hàm số đạt cực đại tại x = -1, fCĐ = f(-1) = 1
Hàm số đạt cực tiểu tại x = 0, fCT = f(0) = 0
Chú ý: mặc dù không tồn tại đạo hàm tại điểm, nhưng hàm số vẫn có thể đạt cực trị tại điểm này.
e) Tập xác định D = R
f’(x) = x4 – x2
f'(x) = 0 ⇔ x = 0 hoặc x = ±1
Bảng biến thiên:
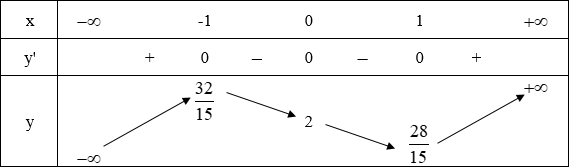
Vậy hàm số đạt cực đại tại x = -1, fCĐ = f(-1) = 32/15 và hàm số cực tiểu tại x = 1; fCT = f(1) = 28/15
f) Tập xác định D = R \ {1}
Ta có: ![]()
f'(x) = 0 ⇔ x = 0 hoặc x = 2.
Bảng biến thiên:
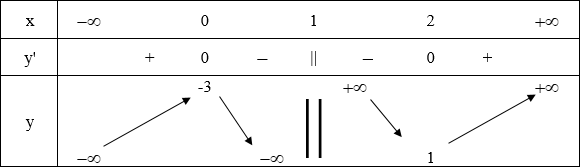
Vậy hàm số cực đại tại x = 0, fCĐ = f(0) = -3 và hàm số cực tiểu tại x = 2; fCT = f(2) = 1
Bài 12 trang 17 SGK
Tìm cực trị của các hàm số sau:

Lời giải:
a) Tập xác định: [-2; 2]
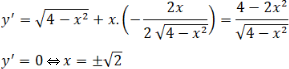
Bảng biến thiên:
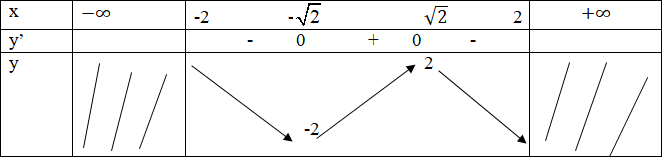
Hàm số đạt cực tiểu tại x = -√2, yCT = y(-√2 ) = -2
Hàm số đạt cực đại tại x = √2, yCĐ = y(√2) = 2
b) Tập xác định: [-2√2; 2√2]
![]()
Bảng biến thiên:
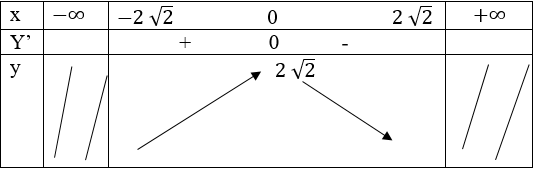
Hàm số cực đại tại x = 0; yCĐ = y(0) = 2√2
Hàm số không có cực tiểu.
c) Tập xác định: R
y' = (x – sin2x + 2)' = 1 – 2 cos2x
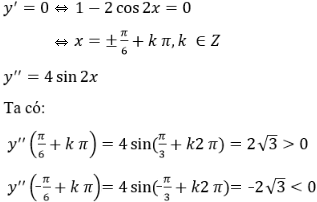
Vậy hàm số cực đại tại điểm
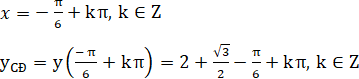
Hàm số đạt cực tiểu tại điểm
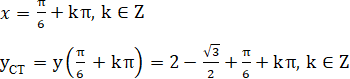
d) Tập xác định: R
y'= 2sinx + 2sin2x = 2sinx(1 + 2cosx )
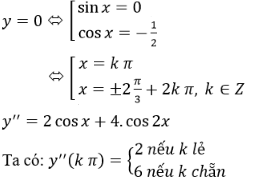
=> y''(kπ) > 0 (có thể viết: y''(kπ) = 4 + 2 cos(kπ)
Nên hàm số đạt cực tiểu tại các điểm
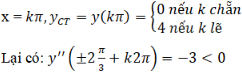
Nên hàm số đạt cực đại tại các điểm
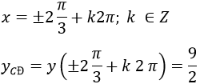
Bài 13 trang 17 SGK
Tìm các hệ số a, b, c, d của hàm số
f(x) = ax3 + bx2 + cx + d
sao cho hàm số đạt cực tiểu tại điểm x = 0; f(0) = 0 đạt cực đại tại điểm x = 1, f(1) = 1.
Lời giải:
Ta có f’(x) = 3ax2 + 2bx + c ⇒ f'(0) = c ; f'(1) = 3a + 2b + c
Vì f(0) = 0 ⇒ d= 0
Hàm số đạt cực tiểu tại x = 0 nên f’(0) = 0 ⇒ c =0; f(1) = a + b = 1
Hàm số đạt cực đại tại điểm x = 1 nên f’(1) = 0 ⇒ 3a + 2b = 0
![]()
Ta được a = -2; b = 3
Vậy f(x) = -2x3 + 3x2
Thử lại f’(x) = -6x2 + 6x; f''(x) = -12x + 6
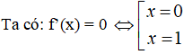
f’(0) > 0. Hàm số đạt cực tiểu tại điểm x = 0
f’(1) = -6 < 0. Hàm số đạt cực đại tại x = 1
Đáp số: a = -2; b = 3; c = 0 ; d = 0
Bài 14 trang 17 SGK
Xác định các hệ số a, b, c sao cho hàm số: (x) = x3 + ax2 + bx + c đạt cực trị bằng 0 tại x = -2 và đồ thị của hàm số đi qua A(1; 0)
Lời giải:
f'(x) = 3x2 + 2ax + b
Điền kiện cần:
Hàm số đạt cực trị bằng 0 tại x = -2 ⇒ f’(-2) = 0 và f(-2) = 0
Hay -4a + b + 12 = 0 (1) và 4a – 2b + c – 8 = 0 (2)
Đồ thị đi qua A(1; 0) ⇒ a + b + c + 1 = 0
Giải hệ Phương trình (1), (2), (3) ta được a = 3; b = 0; c = -4
Điều kiện đủ:
Xét f(x) = x3 + 3x2 – 4. Ta có: đồ thị hàm số f(x) đi qua A(1; 0)
f’(x) = 3x2 + 6x ⇒ f''(x) = 6x + 6
f’(-2) = 0; f’’(2) = -6 < 0 nên x = -2 là điểm cực đại và f(-2) = 0
Đáp số:a = 3; b = 0; c = -4
Bài 15 trang 17 SGK
Chứng minh rằng với mọi giá trị của m, hàm số
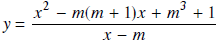
luôn có cực đại và cực tiểu.
Lời giải:
Hàm số được viết lại là:
![]()
Hàm số xác định ∀x ≠ m
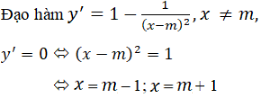
Bảng biến thiên
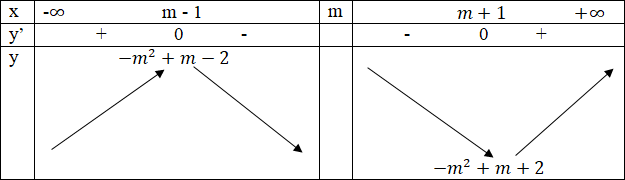
Vậy với mọi giá trị của m, hàm số đạt được cực đại tại x = m – 1 và đạt cực tiểu tại x = m + 1.



































