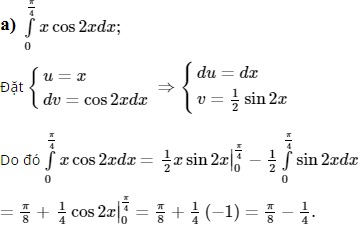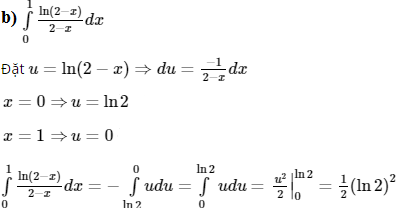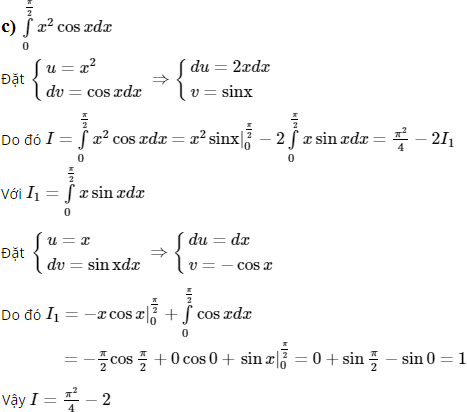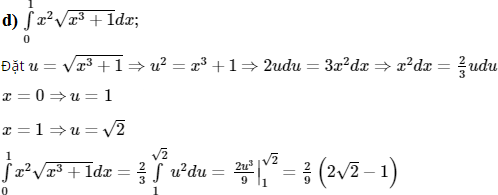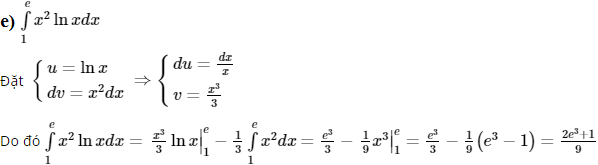Câu hỏi và bài tập
Bài 17 Trang 161 SGK
Dùng phương pháp đổi biến số tính các tích phân sau:
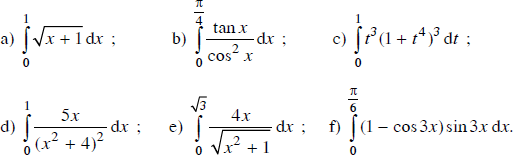
Lời giải:
a) Đặt u = √(x + 1) ⇒ u2 = x + 1 ⇒ 2udu = dx
x = 0 => u = 1; x = 1 ⇒ u = √2
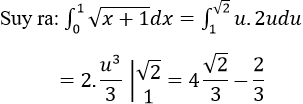
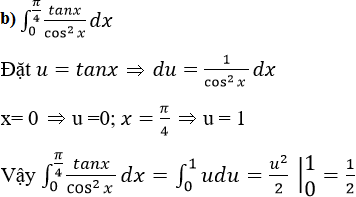
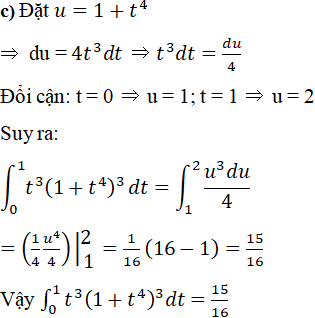
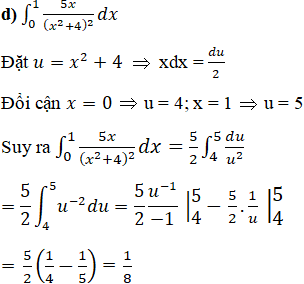
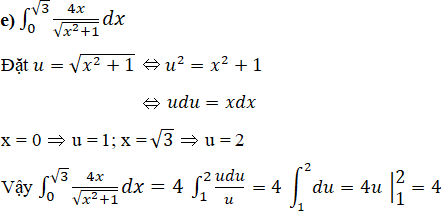
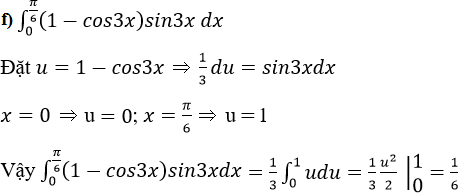
Bài 18 Trang 161 SGK
Dùng phương pháp tích phân từng phần để tính các tích phân sau:

Lời giải:
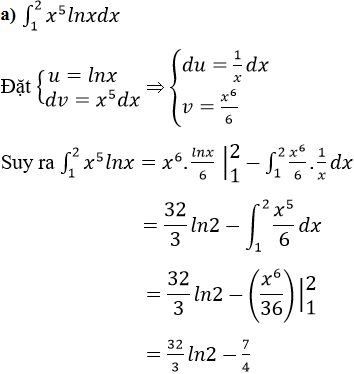
![]()
Đặt u = x + 1; dv = ex dx ⇒ du = dx; v = ex
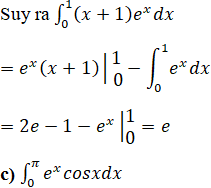
Đặt u = cosx; dv = ex dx ⇒ du = -sinxdx; v = ex
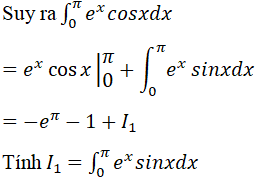
Đặt u1 = sinx; dv = ex dx ⇒ du1 = cosxdx; v = ex
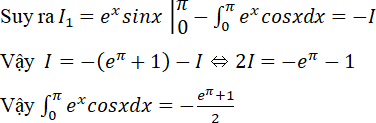
d) Đặt u = x; dv = cosxdx ⇒ du = dx; v = sinx
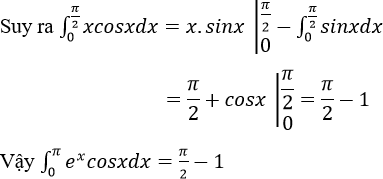
Luyện tập
Bài 19 Trang 161 SGK
Tính
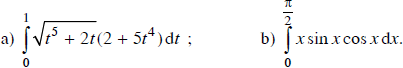
Lời giải:
![]()
⇒ u2 = t5 + 2t ⇒ 2udu = (5t4 + 2)dt
Với t = 0 ⇒ u = 0; t = 1 ⇒ u = √3
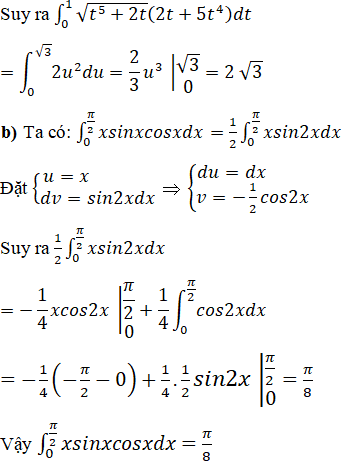
Bài 20 Trang 161 SGK
Tính
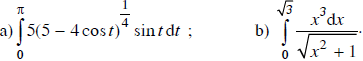
Lời giải:
a) Đặt 5 – 4cost = u ⇒ du = 4sintdt ⇒ sintdt = du/4
t = 0 ⇒ u = 1; t = π ⇒ u = 9
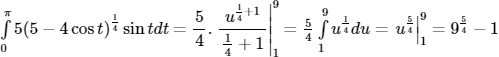
b) Đặt u = √(x2 + 1) ⇒ u2 = x2 + 1 ⇒ udu = xdx ⇒ x3dx = x2.xdx = (u2 − 1)udu
x = 0 ⇒ u = 1; x = √3 ⇒ u = 2
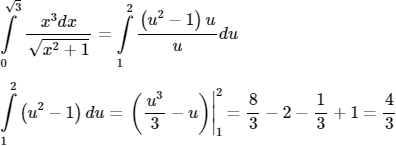
Bài 21 Trang 161 SGK
Giả sử F là một nguyên hàm của hàm số y = sinx/ x trên khoảng (0; +∞).
Khi đó 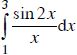 là
là
A. F(3) – F(1); B. F(6) – F(2);
C. F(4) – F(2); D. F(6) = F(4).
Lời giải:
Đặt u = 2x ⇒ du = 2dx ⇒ dx = 1/2du
Đổi cận: x = 1 ⇒ u = 2, x = 3 ⇒ u = 6
![]()
Chọn (B).
Bài 22 Trang 162 SGK
Chứng minh rằng:
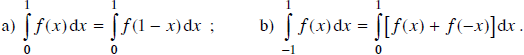
Lời giải:
![]()
Đặt x = 1 – t ⇒ dx = -dt; x = 0 ⇒ t = 1; x = 1 ⇒ t = 0
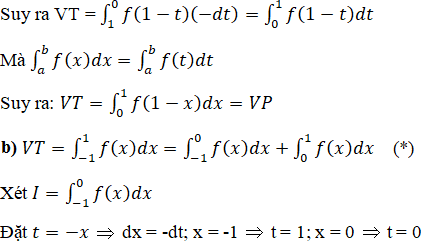
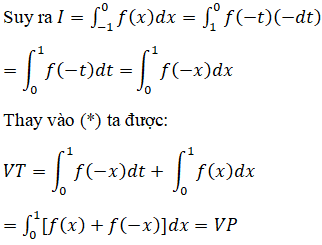
Thay vào (*) ta được:
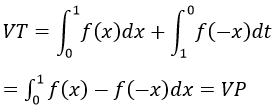
Bài 23 Trang 162 SGK
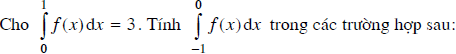
a) f(x) là hàm số lẻ; b) f(x) là hàm số chẵn.
Lời giải:
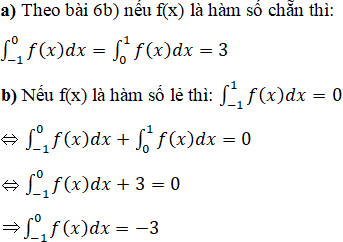
Bài 24 Trang 162 SGK
Tính các tích phân sau:
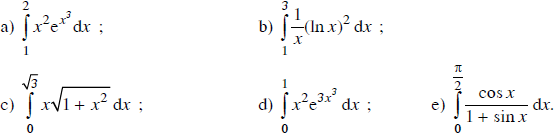
Lời giải:
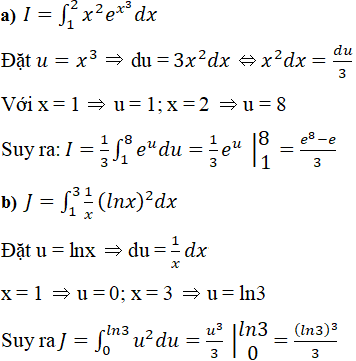
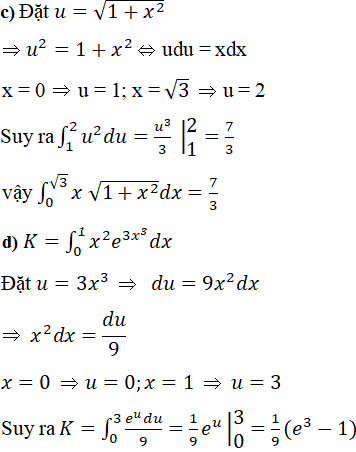
![]()
Đặt u = 1 + sinx ⇒ cosxdx = du; x = 0 ⇒ u = 1; x = π/2 ⇒ u = 2
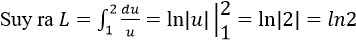
Bài 25 Trang 162 SGK
Tính các tích phân sau:
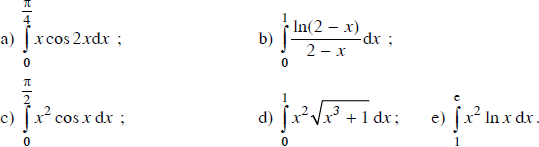
Lời giải: