Câu hỏi và bài tập
Bài 23 trang 89 SGK
Chọn câu khẳng định đúng trong các khẳng định sau.
a) Cơ số của lôgarit là một số thực bất kì.
b) Cơ số của lôgarit phải là số nguyên.
c) Cơ số của lôgarit phải là số nguyên dương.
d) Cơ số của lôgarit phải là số nguyên dương khác 1.
Lời giải:
Câu d, vì theo định nghĩa lôgarit.
Bài 24 trang 89 SGK
Trong các định nghĩa sau khẳng định nào đúng khẳng định nào sai?
a) Có lôgarit của một số thực bất kì;
b) Chỉ có lôgarit của một số thực dương;
c) Chỉ có lôgarit của một số thực dương khác 1;
d) Chỉ có lôgarit của một số thực lớn hơn 1.
Lời giải:
Khẳng định: a) sai b) đúng c) sai d) sai.
Câu a, sai vì không có logarit của số thực nhỏ hơn hoặc bằng 0.
Câu c, sai vì loga1 = 0 với 0 < a ≠ 1.
Câu d, sai vì vẫn có logarit của các số thực trong khoảng (0; 1).
Bài 25 trang 90 SGK
Điền thêm vế còn lại của đẳng thức và bổ sung điều kiện để có đẳng thức đúng.
a) loga(xy) = ⋯; b) … = logax − logay;
c) logaxα = ⋯; d) alogab = ⋯ .
Lời giải:
a) loga(xy) = logax + logay nếu a > 0; a ≠ 1; x > 0; y > 0
b) loga(x/y) = logax − logay nếu a > 0; a ≠ 1; x > 0 và y > 0
c) logaxα = α logax nếu a > 0; a ≠ 1; x > 0
d) alogab = b nếu a > 0; a ≠ 1 và b > 0.
Bài 26 trang 90 SGK
Trong mỗi mệnh đề sau, hãy tìm điều kiện của a để có mệnh đề đúng:
a) logax < logay ⇔ 0 < x < y;
b) logax < logay ⇔ x > y > 0.
Lời giải:
a) a > 1.
b) 0 < a < 1.
Bài 27 trang 90 SGK
Hãy tìm lôgarit của mỗi số sau theo cơ số 3:
![]()
Lời giải:
log33 = 1;
log381 = log334 = 4 log33 = 4;
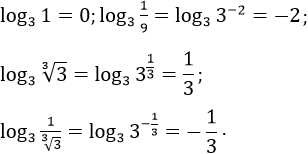
Bài 28 trang 90 SGK
Tính ![]()
Lời giải:
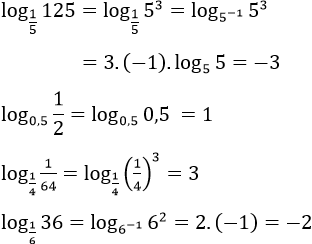
Bài 29 trang 90 SGK
Tính ![]()
Lời giải:
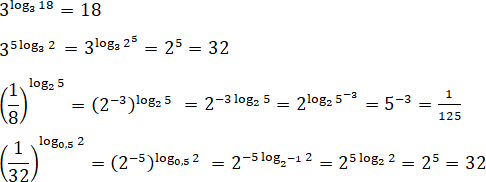
Bài 30 trang 90 SGK
Tìm x, biết:

Lời giải:
a) log5x = 4
Điều kiện: x > 0
Với điều kiện trên phương trình đã cho tương đương: x = 54
b) log2(5 − x) = 3
Điều kiện: x < 5
Với điều kiện trên phương trình đã cho tương đương
5 − x = 23 ⇔ x = 5 − 23 = -3 ( TMĐK)
c) log3(x + 2) = 3
Điều kiện: x > -2
Với điều kiện trên phương trình đã cho tương đương:
x + 2 = 33 ⇔ x = 33 − 2 = 25 (TMĐK)
![]()
Điều kiện: x > -0,5
Với điều kiện trên phương trình đã cho tương đương
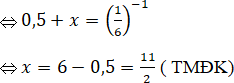
Bài 31 trang 90 SGK
Biểu thị logarit sau đây theo logarit thập phân (rồi cho kết quả bẳng máy tính, làm tròn đến chữ số thập phân thứ 2).
log7 25; log5 8; log9 0,75; log0,75 1,13.
Lời giải:
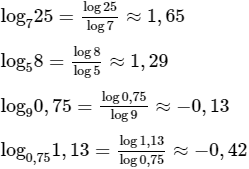
Luyện tập
Bài 32 trang 92 SGK
Hãy tính:
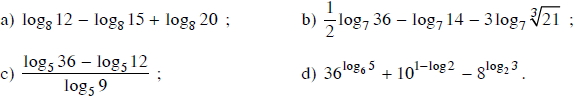
Lời giải:
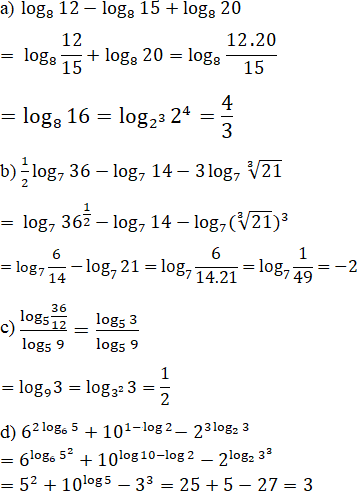
Bài 33 trang 92 SGK
Hãy so sánh:
a) log34 và log4(1/3) b) 3log61,1 và 7log60,99
Lời giải:
a) Ta có: log34 > log33 = 1 và log4(1/3) < log44 = 1
Suy ra, log34 > 1 > log4(1/3)
Vậy log34 > log4(1/3).
b) Ta có: log61,1 > log61 = 0 ⇔ 3log61,1 > 30 = 1
và log60,99 < log61 = 0 ⇔ 7log60,99 < 70 = 1
Suy ra, 3log61,1 > 1 > 7log60,99
Vậy 3log61,1 > 7log60,99.
Bài 34 trang 92 SGK
Không dùng bảng số và máy tính, hãy sánh:
a) log2 + log3 với log5 b) log12 – log 5 với log7
c) 3log2 + log3 với 2log5 d) 1 + 2log3 với log27
Lời giải:
a) Ta có log2 + log3 = log6 > log5
b) log12 – log5 = log(12/5)< log7
c) 3log2 + log3 = log23 + log3 = log(8.3) = log24 < log52 = 2log5
d) 1 + 2log3 = log10 + log32 = log(10.9) = log90 > log27
Bài 35 trang 92 SGK
Trong mỗi trường hợp sau, hãy tính logax, biết logab = 3; logac = -2 :
![]()
Lời giải:
a) logax = loga(a3b2√c)
= logaa3 + logab2 + loga√c
= 3logaa + 2 logab + logac/2
= 3 + 2.3 + (-2)/2 = 8
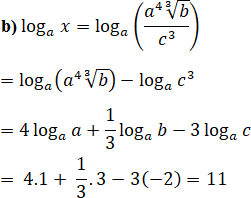
Bài 36 trang 93 SGK
Trong mỗi trường hợp sau, hãy tìm x:
a) log3x = 4log3a + 7 log3b; b) log5x = 2 log5a – 3log5b.
Lời giải:
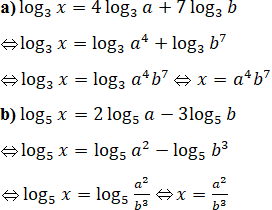
Bài 37 trang 93 SGK
Hãy biểu diễn các lôgarit sau qua α và β
a) log√350 nếu log315 = α; log310 = β;
b) log41250 nếu log25 = α.
Lời giải:
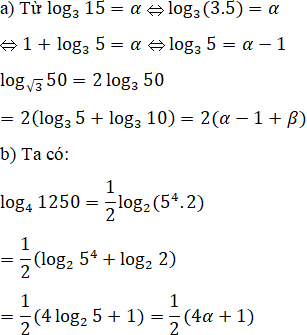
Bài 38 trang 93 SGK
Đơn giản các biểu thức:
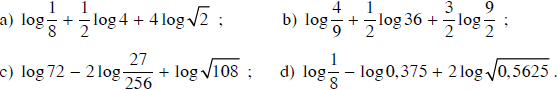
Lời giải:
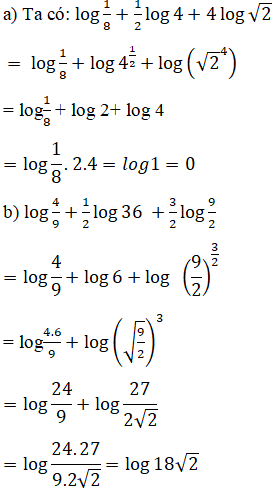
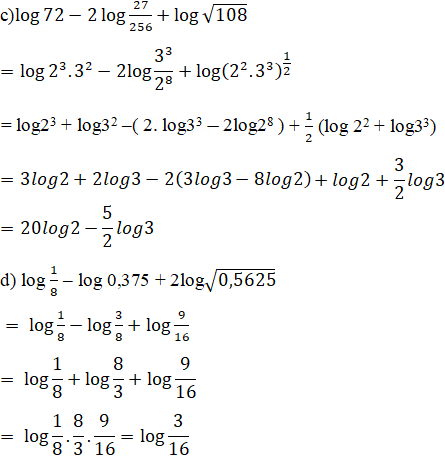
Bài 39 trang 93 SGK
Tìm x, biết:
![]()
Lời giải:

Bài 40 trang 93 SGK
Số nguyên tố dạng Mp = 2p – 1, trong đó p là một số nguyên tố được gọi là số nguyên tố Mec-sen (Mersenne Marin, 1588 – 1648, người pháp).
Ơ - le phát hiện M31 năm 1750.
Luy - Ca (Lucas Edouard, 1842 – 1891, người Pháp) phát hiện M127 năm 1876.
M1398269 được phát hiện năm 1996.
Hỏi rằng nếu viết ba số đó trong hệ thập phân thì mỗi số có bao nhiêu chữ số.
(Dễ thấy rằng số chữ số của 2p – 1 bằng số chữ số của 2p và để tính số chữ số của M127 có thể lấy log2 ≈ 0,30 và để tính số chữ số của M1398269 có thể lấy log2 ≈ 0,30103 (xem ví dụ 8)).
Lời giải:
Ta có: log(2p – 1) = a. Để tính số chữ số của 2p – 1 thì ta tính số chữ số của 2p. Khi viết trong hệ thập phân người ta lấy giá trị gần đúng của log2 là 0,3010.
⇒ Số chữ số của M31 là [31.log2] + 1= [31.0,3010] + 1 = 10
⇒ Số chữ số của M127 là [127.log2] + 1= [127.0,3010] + 1 = 39
⇒ Số chữ số của M1398269 là [1398269.log2] + 1 = [1398269.0,3010] + 1 = 420921
Bài 41 trang 93 SGK
Một người gửi 15 triệu đồng vào ngân hàng theo thể tức lãi kép kì hạn 1 quý với lãi suất 1,65% một quý. Hỏi sau bao lâu người đó có ít nhất 20 triệu đồng (cả vốn lẫn lãi) từ số vốn ban đầu.
Lời giải:
Áp dụng công thức lãi kép ta có: C = A(1 + r)N
Trong đó: A = 15; r = 1,65%, C ≥ 20
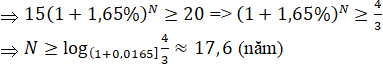
Vậy ít nhất 18 tháng người đó có ít nhất 20 triệu đồng từ số vốn ban đầu.



































