Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.
Bài 98 trang 132 SGK
Giá trị biểu thức log236 − log2144 bằng
(A) – 4; (B) 4; (C) – 2; (D) 2.
Lời giải:
![]()
Chọn (C).
Bài 99 trang 132 SGK
Biết log6√a = 2 thì log6a bằng
(A) 36; (B) 108; (C) 6; (D) 4.
Lời giải:
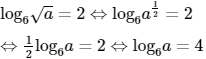
Chọn (D).
Bài 100 trang 132 SGK
Tập số x thỏa mãn log0,4(x – 4) ≥ 0 là
A. (4; +∞); B. (4; 6,5); C. (-∞; 6,5); D. [6,5; +∞).
Lời giải:
log0,4(x – 4) ≥ -1 ⇔ 0 < x − 4 ≤ 0,4 − 1 ⇔ 4 < x ≤ 6,5.
Chọn (B).
Bài 101 trang 132 SGK
Tập các số x thỏa mãn 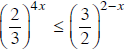 là
là
(A) (−∞; 2/3];
(B) [−2/3; +∞);
(C) (−∞; 2/5];
(D) [2/5; +∞).
Lời giải:
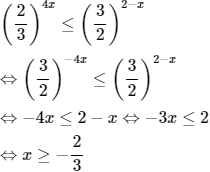
Chọn (B).
Bài 102 trang 133 SGK
Giá trị biểu thức 3 log0,1102,4 bằng
(A) 0,8; (B) 7,2; (C) -7,2; (D) 72.
Lời giải:
![]()
Chọn (C).
Bài 103 trang 133 SGK
Giá trị của biểu thức (0,5) log225 + log2(1,6) bằng
(A) 1; (B) 2; (C) 3; (D) 5.
Lời giải:
(0,5) log225 + log2(1,6)〗= log25 + log28 – log25 = 3.
Chọn (C).
Bài 104 trang 133 SGK
Giá trị của biểu thức bằng
(A) 4; (B) 3; (C) 1; (D) -8.
Lời giải:
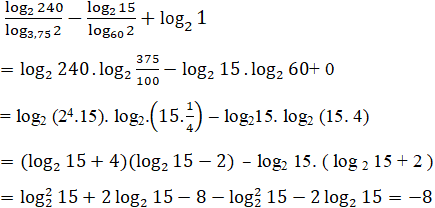
Chọn (D).
Bài 105 trang 133 SGK
Tập các số x thỏa mãn 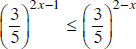 là
là
A. [3; +∞); B. (-∞; 1]; C. [1; +∞); D. (-∞; +∞).
Lời giải:
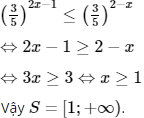
Chọn (C).
Bài 106 trang 133 SGK
Đối với hàm số f(x) = ecos2x, ta có
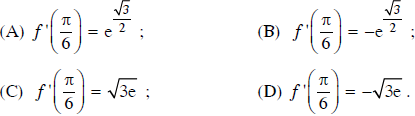
Lời giải:
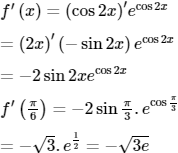
Chọn (D).
Bài 107 trang 133 SGK
Đối với hàm số , ta có
(A) xy' + 1 = ey;
(B) xy' + 1 = -ex;
(C) x'y – 1 = ey;
(D) xy' – 1 = -ey.
Lời giải:
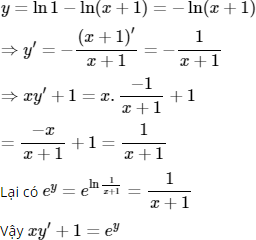
Chọn (A).
Bài 108 trang 133 SGK
Trên hình 2.13, đồ thị của ba hàm số
y = ax; y = bx; y = cx
(a, b và c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c.
(A) a > b > c; (B) a > c > b;
(C) b > a > c; (D) b > c > a.
Lời giải:
Hàm số y = ax đồng biến trên R nên a > 1.
Hàm số y = bx, y = cx nghịch biến trên R nên 0 < b, c < 1.
Với x > 0 thì bx < cx ⇒ b < c.
Vậy b < c < a.
Chọn (B).
Bài 109 trang 133 SGK
Trên hình 2.14, đồ thị của ba hàm số
y = logax; y = logbx; y = logcx
(a, b, c dương khác 1) được vẽ trên cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của logarit, hãy so sánh 3 số a, b, c.
(A) a > b > c; (B) c > a > b;
(C) b > a > c; (D) c > b > a.
Lời giải:
Với x > 0 thì hàm số y = logcx nghịch biến nên 0 < c < 1.
Với x > 0 thì hai hàm số y = logax và y = logbx đồng biến nên a > 1; b > 1.
Dựa vào đồ thị với x > 1, ta có logax > logbx nên a < b.
Vậy c < a < b.
Chọn (C).
Bài 110 trang 133 SGK
Phương trình
có bao nhiêu nghiệm?
(A) 1 nghiệm; (B) 2 nghiệm; (C) 3 nghiệm; (D) vô nghiệm.
Lời giải:
Điều kiện: x > 0; x ≠ 2.
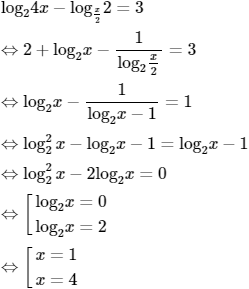
Chọn (B).



































