Câu hỏi và bài tập
Bài 49 trang 49 SGK
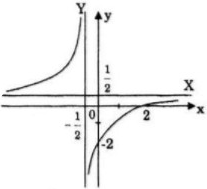
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
![]()
b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đồ thị là tâm đối xứng của đồ thị.
Lời giải:
a) ![]()
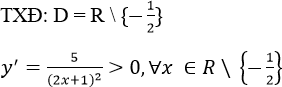
Suy ra, hàm số đồng biến trên khoảng (-∞; -1/2) và (1/2; +∞ )
Hàm số không có cực trị.
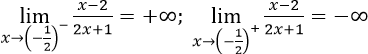
Vậy đường thẳng x = -1/2 là tiệm cận đứng.
![]()
Vậy đường thẳng y = 1/2 là tiệm cạn ngang.
Bảng biến thiên
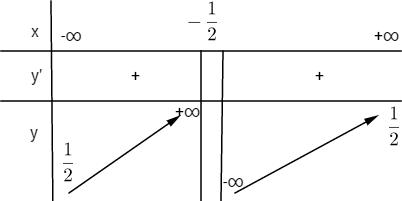
Đồ thị
+ Giao với Ox là A(2; 0).
+ Giao với Oy là B(0; -2).
b) Giao điểm của hai tiệm cận
![]()
Áp dụng công thức đổi trục tọa độ
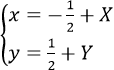
Khi đó hàm số đã cho trở thành
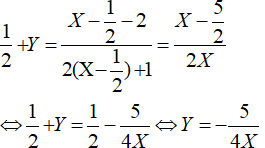
Đây là hàm số lẻ nên đồ thị có tâm đối xứng là điểm I ⇒ điều phải chứng minh.
Bài 50 trang 49 SGK
Khảo sát sự biến thiên và vẽ đồ thị hàm số sau
![]()
Lời giải:
a) ![]()
TXĐ: D = R \ {1}
![]()
Suy ra, hàm số luôn nghịch biến trên (-∞; 1) và (1; +∞)
Hàm số không có cực trị.
Lại có:
![]()
Vậy đường thẳng x = 1 là tiệm cận đứng.
![]()
Do đó đồ thị hàm số nhận đường thẳng y = 1 làm tiệm cận ngang.
Bảng biến thiên
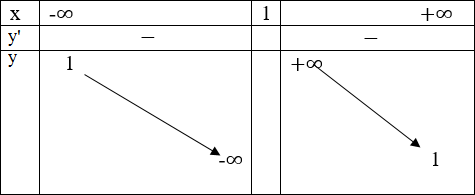
Đồ thị
+ Giao với Ox là A(-1; 0)
+ Giao với Oy là B(0; -1)
Đồ thị nhận I(1; 1) làm tâm đối xứng.
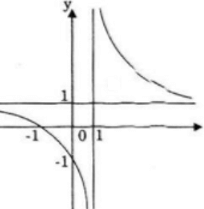
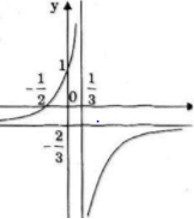
b) ![]()
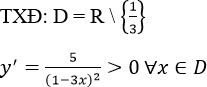
Hàm số luôn đồng biến trên (-∞; 1/3) và (1/3; +∞)
Hàm số không có cực trị.
![]()
Vậy đường thẳng y = -2/3 là tiệm cận ngang
![]()
Vậy đường thẳng x = 1/3 là tiệm cận đứng.
Bảng biến thiên

Đồ thị
+ Giao với Ox là A(-1/2; 0)
+ Giao với Oy là B(0; 1)
Đồ thị nhận I(1/3; -2/3) làm tâm đối xứng.
Bài 51 trang 49 SGK
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
![]()
b) Chứng minh rằng giao điểm I của đường tiệm cận của đồ thị là tâm đối xứng của đồ thị.
c) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình
![]()
Lời giải:
a) ![]()
TXĐ: D = R \{-2}
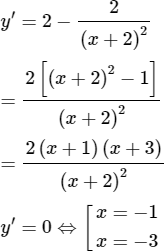
Hàm số đồng biến trên khoảng (-∞; -3) và (-1; +∞)
Hàm số nghịch biến trên (-3; -2) và (-2; -1)
yCĐ = y(-3) = -7
yCT = y(-1) = 1
![]()
Vậy đường thẳng x = -2 là tiệm cận đứng.
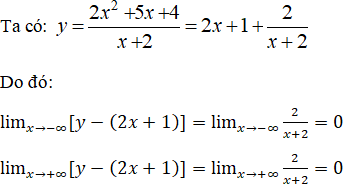
Vậy đường thẳng y = 2x + 1 là tiệm cận xiên.
Bảng biến thiên
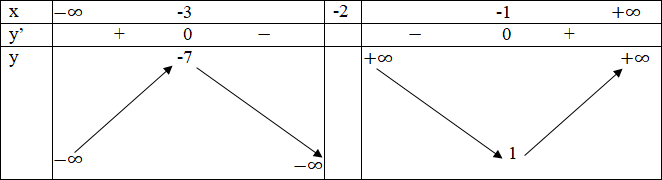
Đồ thị giao với Oy là A(0; 2)
Đi qua B(-1; 1)
b) Giao điểm của 2 đường tiệm cận là nghiệm của hệ
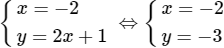
Vậy I(-2; -3).
Áp dụng công thức trục tọa độ
![]()
Khi đó, hàm số đã cho có phương trình
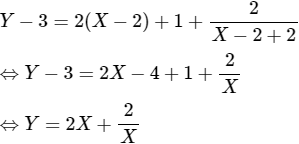
Đây là hàm số lẻ nên đồ thị có tâm đối xứng là điểm I.
c) Xét phương trình 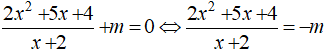
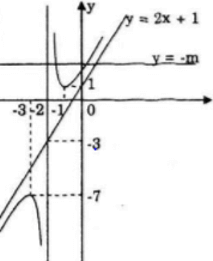
Suy ra, số nghiệm của phương trình chính là số giao điểm của đồ thị hàm số ![]() và đường thẳng y = - m.
và đường thẳng y = - m.
Dựa vào đồ thị hàm số ![]() ta có:
ta có:
+ -m > 1 ⇔ m < -1, đường thẳng y = -m cắt đồ thị tại 2 điểm ⇒ Phương trình có 2 nghiệm phân biệt.
+ -7 < -m < 1 ⇔ -1 < m < 7, đường thẳng y = -m không cắt đồ thị ⇒ Phương trình vô nghiệm.
+ -m < -7 ⇔ m > 7, đường thẳng y = -m cắt đồ thị tại 2 điểm ⇒ Phương trình có 2 nghiệm phân biệt.
+ Nếu ![]() thì đường thẳng y = -m cắt đồ thị hàm số tại 1 điểm.
thì đường thẳng y = -m cắt đồ thị hàm số tại 1 điểm.
Kết luận:
• m < -1 hoặc m > 7 thì phương trình có 2 nghiệm phân biệt.
• m = -1 hoặc m = 7 thì phương trình có 1 nghiệm.
• -1 < m < 7 thì phương trình vô nghiệm.
Bài 52 trang 50 SGK
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

Lời giải:
a) ![]()
TXĐ: D = R \ {1}
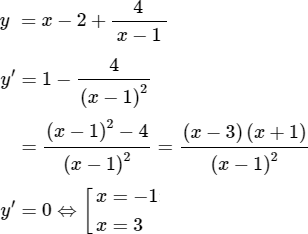
Hàm số đồng biến trên khoảng (-∞; -1) và (3; +∞)
Hàm số nghịch biến trên khoảng (-1; 1) và (1; 3)
yCĐ = y(-1) = -5; yCT = y(3 ) = 3
![]()
Vậy đường thẳng x = 1 làm tiệm cận đứng.
Bảng biến thiên
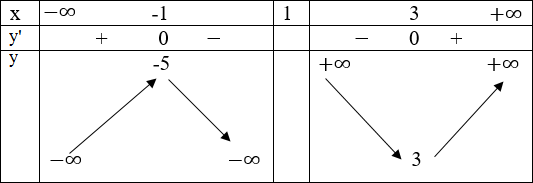
Đồ thị
+ Giao với Oy (0; -6)
+ Đi qua A(-3; -6)
Đồ thị nhận giao điểm I (1; −1) của hai đường tiệm cận làm tâm đối xứng.

b) ![]()
TXĐ: D = R \ {1}
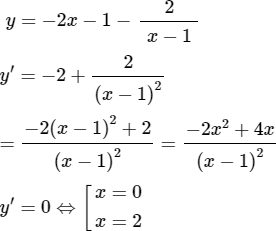
Hàm số đồng biến trên khoảng (0; 1)và (1; 2)
Hàm số nghịch biến trên khoảng (-∞, 0) và (2; +∞)
yCĐ = y(2) = -7; yCT = y(0) = 1
![]()
Vậy đường thẳng x = 1 làm tiệm cận đứng.
Bảng biến thiên
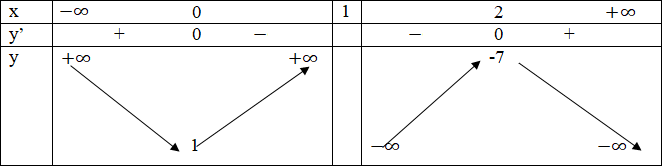
Đồ thị đi qua điểm A(-1; 2) và B(2; -7)
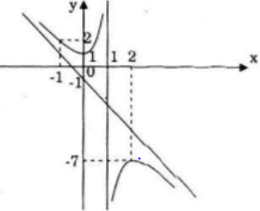
c) ![]()
TXĐ: D = R \ {-2}
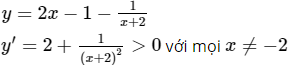
Vậy hàm số luôn đồng biến trên khoảng (-∞; -2) và (-2; +∞)
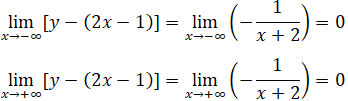
Vậy đường thẳng y = 2x – 1 là tiệm cận xiên.
Bảng biến thiên
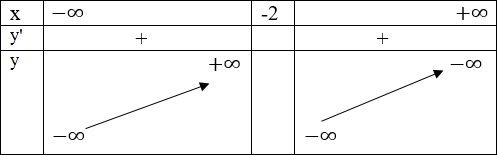
Đồ thị
+ Giao với Oy A(0; -3/2)
+ Đi qua B(-1; -4)
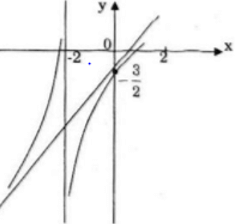
d) ![]()
TXĐ: D = R \ {1}
![]()
Vậy hàm số luôn nghịch biến trên (-∞;1) và 1; +∞)
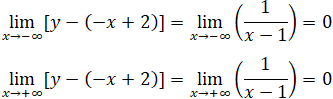
Vậy đường thẳng y = -x + 2 là tiệm cận xiên
![]()
Vậy đường thẳng x = 1 là tiệm cận đứng.
Bảng biến thiên.
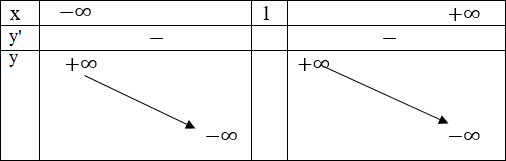
Hàm số đi qua A(0; 1) và B(2; 1)
Luyện tập
Bài 53 trang 50 SGK
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số ![]()
b) Viết phương trình tiếp tuyến của đồ thị hám số đã cho tại giao điểm A của đồ thị với trục tung.
c) Viết phương trinh tiếp tuyến của đồ thị song song với tiếp tuyến tại điểm A.
Lời giải:
a) ![]()
TXĐ: D = R \ {2}
![]()
Vậy hàm số đã cho luôn nghịch biến trên (-∞,2) và (2; +∞)
![]()
Vậy x = 2 là tiệm cận ngang.
Lại có:
![]()
Do đó, đồ thị hàm số nhận đường thẳng y =1 làm tiệm cận ngang
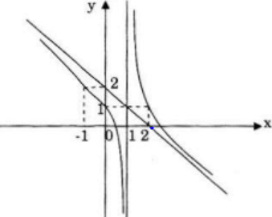
Bảng biến thiên
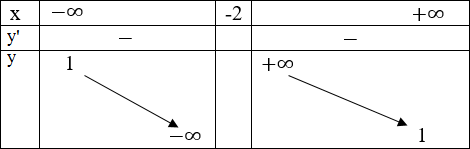
Đặc biệt A(0; - 1/2); B(-1; 0)
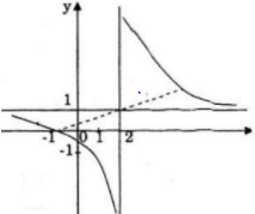
b) Giao điểm của đồ thị với trục tung A(0; -1/2)
![]()
Phương trình tiếp tuyến tại A có dạng
![]()
c) Giả sử M là tiếp điểm của tiếp tuyến song song với tiếp tuyến tại A ta có:
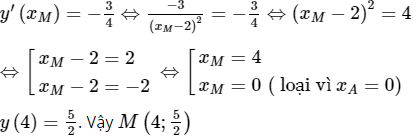
Phương trình tiếp tuyến tại điểm M là: ![]()
Bài 54 trang 50 SGK
a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số ![]()
b) Từ đồ thị (H) suy ra cách vẽ đồ thị của hàm số ![]()
Lời giải:
a) ![]()
TXĐ: D = R∖{−1}
Tiệm cận đứng x = −1 vì:
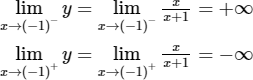
Tiệm cận ngang y = 1 vì:
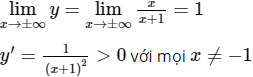
nên hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).
Bảng biến thiên
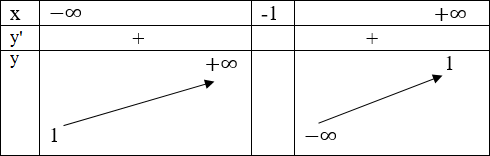
Điểm đặc biệt A(0; 0); B(1; 1/2).
Đồ thị nhận I(-1; 1) làm tâm đối xứng.
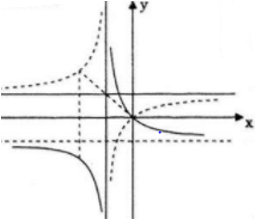
b)
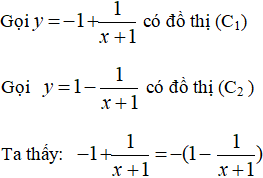
⇒ Cách vẽ đồ thị (C1):
Lấy đối xứng đồ thị (C2) qua trục hoành ta được đồ thị (C1).

Bài 55 trang 50 SGK
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số ![]()
b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm (3; 3).
Lời giải:
a) ![]()
Tập xác định: D = R∖{1}
![]()
Vậy hàm số luôn đồng biến trên (-∞;1) và (1; +∞)
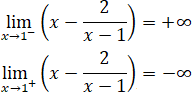
Vậy đường thẳng x = 1 là tiệm cận đứng.
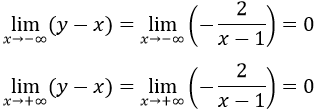
Bảng biến thiên

Đồ thị
Giao với Ox: (-1; 0); (2; 0)
Giao với Oy: (0; 2)
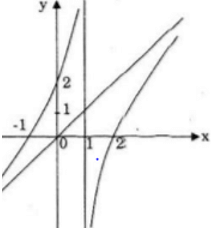
b) Gọi phương trình đường thẳng (d) có hệ số góc k đi qua A(3; 3) có dạng y – 3 = k(x – 3) ⇔ y = k(x – 3) + 3
(d) là tiếp tuyến của đồ thị hàm số khi và chỉ khi hệ Phương trình sau có nghiệm”
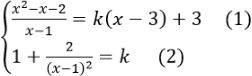
Thế (2) vào (1) ta được:
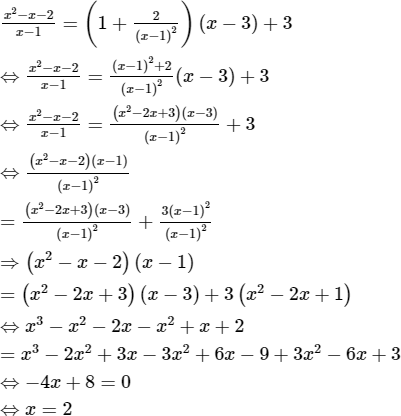
Với x = 2 thay vào (2) ta được k = 3.
Vậy phương trình tiếp tuyến là y = 3(x – 3) + 3 hay y = 3x – 6
Bài 56 trang 50 SGK
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ![]()
b) Từ đồ thị (C) suy ra cách vẽ đồ thị của hàm số ![]()
Lời giải:
a) ![]()
TXĐ: D = R \ {-1}
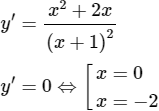
Hàm số đồng biến trên khoảng (-∞; -2) và (0; +∞)
Hàm số nghịch biến trên (-2; -1) và (-1; 0)
yCĐ = y(-2) = -4; yCT = y(0) = 0
![]()
Vậy đường thẳng x = -1 là tiệm cận đứng.
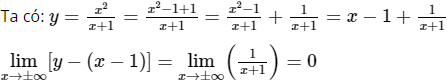
Vậy đường thẳng y = x – 1 là tiệm cận xiên
Bảng biến thiên

Đồ thị
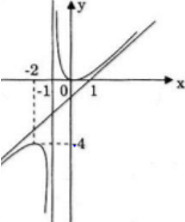
b) Ta có:
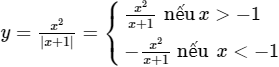
Do đó cách dựng:
- Giữ nguyên phần đồ thị (C) ở bên phải tiệm cận đứng x = −1
- Lấy đối xứng của phần (C) bên trái tiệm cận đứng qua trục hoành.
- Hợp hai phần đồ thị này ta được đồ thị hàm số cần tìm.