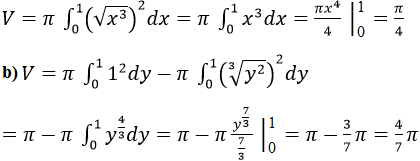Tìm nguyên hàm của các hàm số sau (từ bài 41 đến bài 43):
Bài 41 Trang 175 SGK
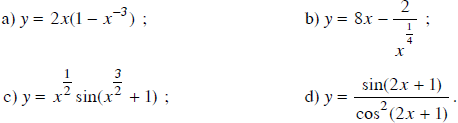
Lời giải:
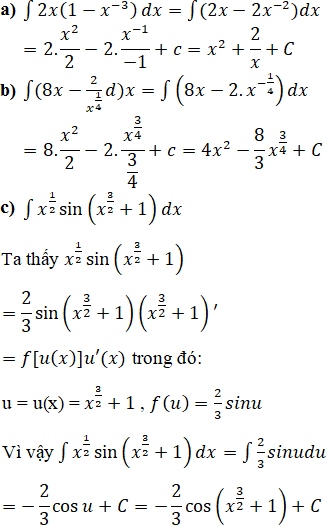
Chú ý: ta có thể tìm nguyên hàm này theo cách không đưa ra biến u như sau:
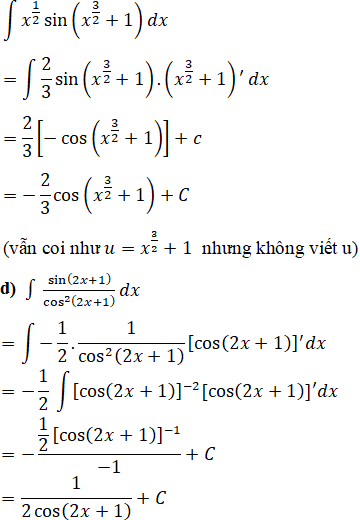
Bài 42 Trang 175 SGK
Lời giải:
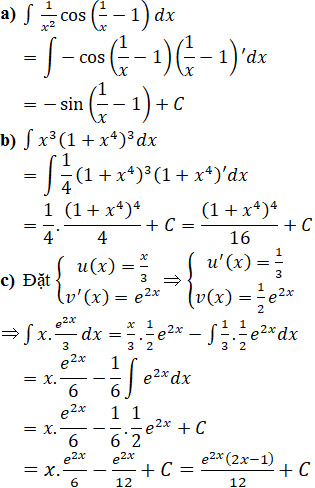
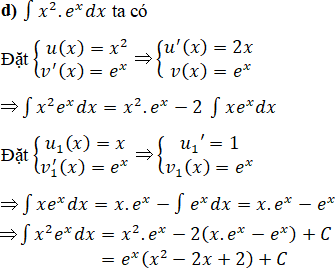
Bài 43 Trang 176 SGK
a) y = xe-x ; b) y = lnx/x .
Lời giải:
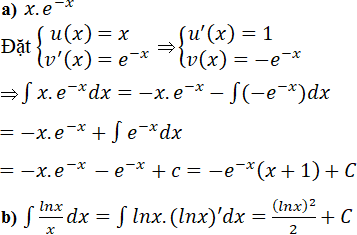
Bài 44 Trang 176 SGK
Tìm hàm số y = f(x) nếu biết dy = 12x(3x2 – 1)3 dx và f(1) = 3
Lời giải:
Theo định nghĩa nguyên hàm thì f(x) là một nguyên hàm của hàm g(x) = 12x(3x2 – 1)3
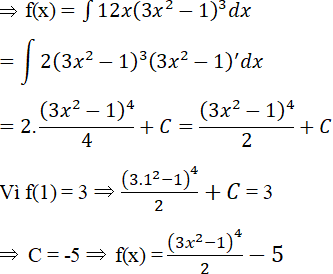
Bài 45 Trang 176 SGK
Xác định số b dương để tích phân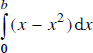 
có giá trị lớn nhất:
Lời giải:
Từ bảng biến thiên ta thấy y lớn nhất bằng 1/6 khi x = 1.
Vậy để tích phân I có giá trị lớn nhất khi b = 1.
Bài 46 Trang 176 SGK
Cho biết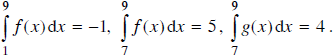 
Hãy tìm
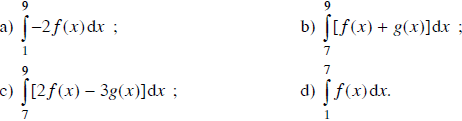
Lời giải:
Áp dụng tính chất cở bản của nguyên hàm ta có:
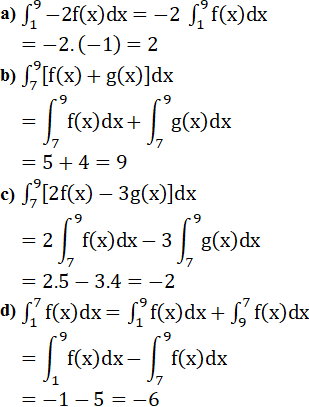
Bài 47 Trang 176 SGK
Cho hàm số f(x) liên tục trên [a; b]. Tỉ số
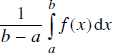
được gọi là giá trị trung bình của hàm số f(x) trên [a; b] và được kí hiệu m(f). Chứng minh rằng tồn tại điểm c ∈ [a; b] sao cho m(f) = f(c).
Lời giải:
Ta có:
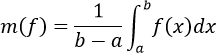
Gọi F(x) là một nguyên hàm của f(x) ⇒ F’(x) = f(x) ⇒ F(x) liên tục trên [a; b] có đạo hàm trên (a; b) và thỏa mãn:
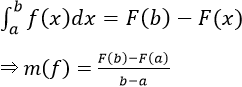
Theo định lý Lagrăng thì ∃c ∈ (a; b) sao cho
Vì F' (c) = f(c) ⇒ ∃c ∈ (a; b) để m(f) = f(c) (đpcm)
Bài 48 Trang 176 SGK
Giả sử một vật từ trạng thái nghỉ khi t = 0 (s) chuyển động thẳng với vận tốc v(t) = t(5 – t) (m/s). Tìm quãng đường vật đi được cho tới khi nó dừng lại.
Lời giải:
Khi vật dừng lại nghĩa là:
⇒ Sau 5 giây thì vật dừng lại. Vậy quãng đường vật đi được là:
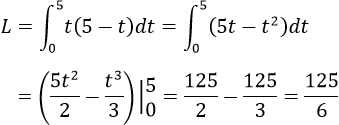
Bài 49 Trang 176 SGK
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau đạt đến vận tốc 6m/s. Từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. Biết rằng B đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Lời giải:
Từ công thức v1 = v0 + at ta có:
Gia tốc trọng trong 8 giây đầu của chất điểm A là:
⇒ Phương trình vận tốc của chuyển động có dạng:
Tại t = 0 thì v(0) = 0 nên C = 0.
Do đó, phương trình chuyển động của vật là: 
Trong 8 giây đầu này, chất điểm A chuyển động nhanh dần với vận tốc v(t) = 3t/4 , vậy nó đi được quãng đường là
Sau 12 giây tiếp theo ( khi mà bị B đuổi kịp A), A đi được thêm 6.12 = 72 mét.
Như vậy, khi bị B đuổi kịp, A và B đi được quãng đường là 24 + 72 = 96 mét
Từ công thức
Suy ra gia tốc của chất điểm B là:
Vậy khi đuổi kịp A, vận tốc của b là:
v1 = v0 + at = 0 + 3.8 = 24 (m/s)
Bài 50 Trang 176 SGK
Tính các tích phân sau:
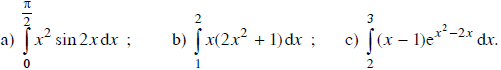
Lời giải:
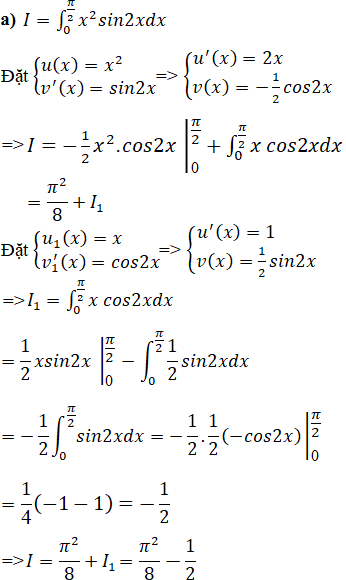
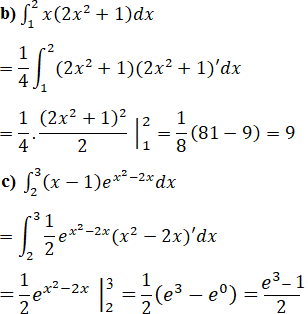
Bài 51 Trang 176 SGK
Tính diện tích các hình phẳng giới hạn bởi:
a) Đồ thị các hàm số y = 4 – x2; y = -x + 2
b) Các đường cong có Phương trình x = 4 – 4y2 và x = 1 – y4 trong miền x ≥ 0.
Lời giải:
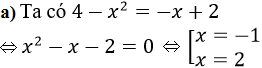
Vậy diện tích hình phẳng cần tìm là:
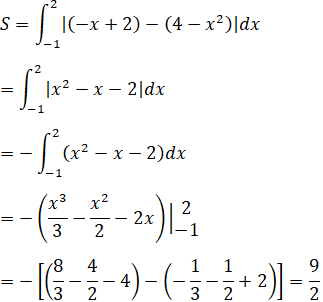
b) Tung độ giao điểm của hai đường cong là nghiệm của phương trình
4 – 4y2 = 1 – y4 ⇔ y4 – 4y4 + 3 = 0
Xét dấu (y2 – 1)(y2 – 3) ta có
| y | –∞ | -√3 | -1 | 1 | √3 | +∞ | |||||
| y2 – 1 | + | | | + | 0 | – | 0 | + | | | + | ||
| y2 – 3 | + | 0 | – | | | – | | | – | 0 | + | ||
| (y2 – 1)(y2 – 3) | + | 0 | – | 0 | + | 0 | – | 0 | + |
Bài 52 Trang 177 SGK
Tính diện tích của các hình phẳng giới hạn bởi
a) Parabol y = x2 – 2x + 2, tiếp tuyến nó tại điểm M(3; 5) và trục tung.
b) Parabol y = -x2 + 4x – 3 và các tiếp tuyến của nó tại các điểm A(0; -3) và B(3; 0).
Lời giải:
a) y = x2 – 2x + 2
y'= 2x – 2;y' (3) = 4
⇒ Phương trình tiếp tuyến tại M là:
y – 5 = 4(x –3) hay y = 4x – 7
Diện tích cần tìm là:
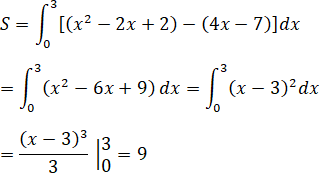
b) y = -x2 + 4x – 3
y' = -2x + 4
y' (3) = -2 và y’(0) = 4
Tiếp tuyến tại A là: y = 4x – 3
Tiếp tuyến tại B là: y = -2x + 6
Hai tiếp tuyến này cắt nhau tại điểm có hoành độ là nghiệm của phương trình.
4x – 3 = -2x + 6 ⇔ x = 3/2
Dựa vào hình vẽ ta có diện tích cần tìm là:
Bài 53 Trang 177 SGK
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 2 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2) là một nửa hình tròn đường kính √5 x2.
Lời giải:
Thiết diện của vật thể có diện tích là:
Vậy thể tích cần tìm là:
Bài 54 Trang 177 SGK
Xét hình giới hạn đường hyperbol y = 2/x và các đường thẳng y = 1; y = 4; x = 0. Tính thể tích của khối tròn xoay tạo thành khi quay hình đó quanh trục tung.
Lời giải:
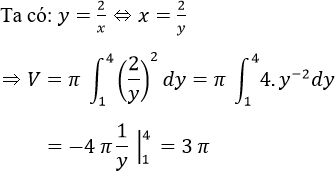
Bài 55 Trang 177 SGK
Cho hình phẳng A được giới hạn bởi đồ thị hàm số
và hai trục tọa độ. Tính thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành.
Lời giải:
Hoành độ giao điểm của hàm số y = √cosx (0 ≤ x ≤ π/2) với trục hoành là nghiệm phương trình:
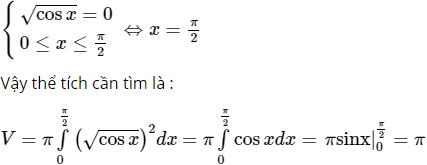
Bài 56 Trang 177 SGK
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x(y + 1) = 2 và các đường thẳng x = 0; y = 0; y = 3. Tính thể tích khối tròn xoay tạo được khi quay A quanh trục tung.
Lời giải:
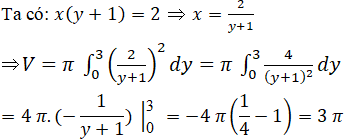
Bài 57 Trang 177 SGK
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x − y2 = 0 và các đường thẳng y = 2, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay A
a) Quanh trục hoành.
b) Quanh trục tung.
Lời giải:
a) Đồ thị hàm số y = √x cắt đường thẳng y = 2 tại điểm có hoành độ là 4.
Thể tích khối tròn xoay tạo được bằng thể tích khối tròn xoay tạo thành khi quay miền hình chữ nhật OMNP quanh Ox trừ đi thể tích khối tròn xoay tạo thành khi quay miền tam giác cong ONP quanh Ox.
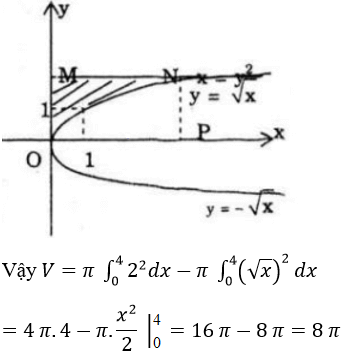
b) Thể tích cần tìm là:
Bài 58 Trang 177 SGK
Cho hình phẳng A giới hạn bởi đường cong y = x1/2 ex/2 và các đường thẳng x = 1; x = 2, y = 0. Tính thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành.
Lời giải:
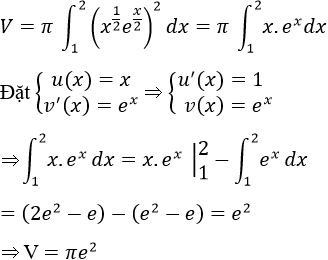
Bài 59 Trang 177 SGK
Cho hình phẳng A được giới hạn bởi đường cong có phương trình y2 = x3 và các phương trình y = 0; x = 1 trong miền y ≥ 0. Tính thể tích khối tròn xoay được khi quay A
a) Quanh trục hoành.
b) Quanh trục tung.
Lời giải:
y2 = x3 ⇔ y = ±√(x3 ) ⇔ x = ∛(y2 )
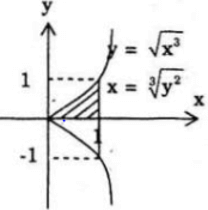
a) Ta thấy đường cong y2 = x3 có 2 nhánh đối xứng qua Ox.
Vậy khi quay quanh trục hoành ta có vật thể xoay tròn có thể tích:
