Câu hỏi và bài tập
Bài 1 trang 189 SGK
Cho số phức
2 + 3i; 1 + 2i; 2 − i.
a) Biểu diễn các số trong mặt phẳng số phức.
b) Viết số phức liên hợp của mỗi số đó và biểu diễn chúng trong mặt phẳng phức.
c) Viết đối số của mỗi số phức và biểu diễn chúng trong mặt phẳng phức.
Lời giải:
a) Các điểm A, B, C lần lượt biểu diễn các số phức 1 + 2i; 2 + 3i; 2 – i
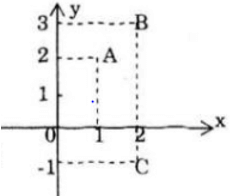
b) Số phức liên hợp của 2 + 3i là: 2 − 3i
Số phức liên hợp của 1 + 2i là: 1 − 2i
Số phức liên hợp của 2 − i là: 2 + i
Các điểm M, N, P lần lượt biểu diễn các số phức: 2 − 3i, 1 − 2i, 2 +i.
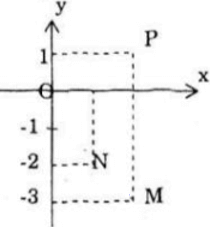
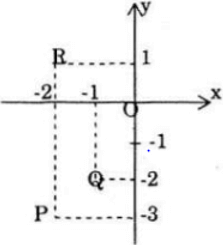
c) Các số đối của 2 + 3i; 1 + 2i và 2 – i lần lượt là: −2 – 3i; −1 – 2i và −2 + i được biểu diễn bởi các điểm: P, Q, R.
Bài 2 trang 189 SGK
Xác định phần thực và phần thực của các số sau:
a) i + (2 − 4i) − (3 −2i);
b) (√2 + 3i)2;
c) (2 + 3i)(2 − 3i);
d) i(2 − i)(3 + i).
Lời giải:
a) Ta có:
i + (2 − 4i) − (3 −2i)
= i + 2 − 4i − 3 + 2i
= −1 − i
Có phần thực bằng −1; phần ảo bằng −1.
b) (√2 + 3i)2
= 2 + 6√2i + 9i2
= 2 + 6√2i − 9
= −7 + 6√2i
Có phần thực bằng −7, phần ảo bằng 6√2.
c) (2 + 3i)(2 − 3i)
= 4 − 9i2
= 4 + 9 = 13
Có phần thực bằng 13, phần ảo bằng 0.
d) i(2 − i)(3 + i)
= (2i + 1)(3 + i)
= 6i + 2i2 + 3 + i
= 1 + 7i
Có phần thực bằng 1, phần ảo bằng 7.
Bài 3 trang 189 SGK
Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ O trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.
Lời giải:
Gọi lục giác đều là ABCDEF, trong đó A là biểu diễn cho số i.
Suy ra A(0; 1) và góc AOB = 600 (hình vẽ)
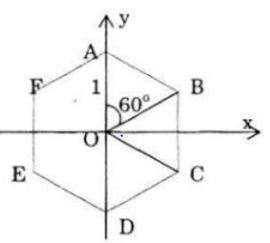
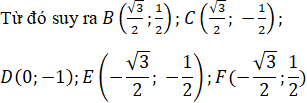
Vậy sáu số phức cần tìm là:
![]()
Bài 4 trang 189 SGK
Thực hiện phép tính:
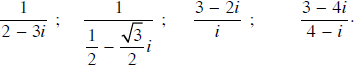
Lời giải:
Nhân cả tử và mẫu của số đã cho với lượng liên hợp ở mẫu ta được.
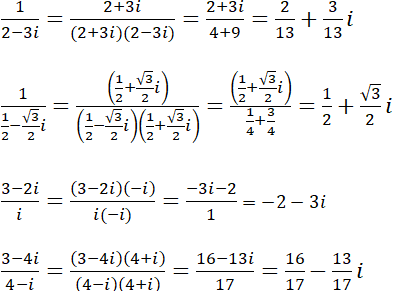
Bài 5 trang 190 SGK
Cho ![]()
Hãy tính ![]()
Lời giải:
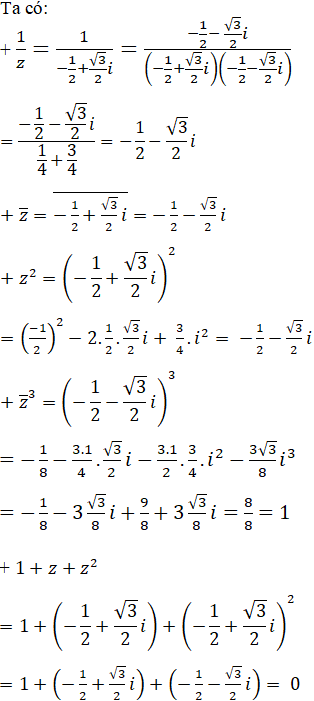
Bài 6 trang 190 SGK
Chứng minh rằng:
a) Phần thực của số phức z bằng
phần ảo của số phức z bằng
b) Số phức z là phần ảo khi và chỉ khi
c) Với mọi số phức z, z’, ta có
và nếu z # 0 thì
Lời giải:
a)
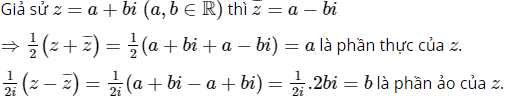
b) z là số ảo khi và chỉ khi phần thực của z bằng 0
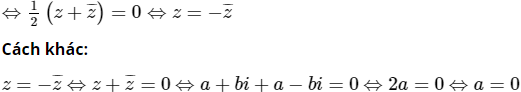
c) Giả sử z = a + bi; z′ = a′ + b′i (a, b, a′, b′ ∈ R)
Ta có:
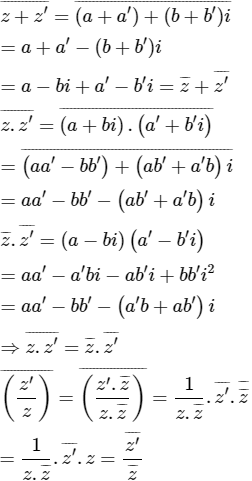
Bài 7 trang 190 SGK
Chứng minh rằng với mọi số nguyên m > 0, ta có:
i4m = 1; i4m + 1 = i; i4m + 2 = -1; i4m + 3 = -i.
Lời giải:
Ta có: i4m = (i2)2m = (-1)2m = 1, với ∀m ∈ N*
i4m + 1 = i4m.i = 1.i = i
i4m + 2 = i4m.i2 = 1.(-1) = -1
i4m + 3 = i4m.i3 = 1.i3 = i3 = i2.i = -1.i = -i (đpcm)
Bài 8 trang 190 SGK
Chứng minh rằng:
a) Nếu vectơ ![]() của một mặt phẳng phức biểu diễn số phức z thì độ dài của vectơ
của một mặt phẳng phức biểu diễn số phức z thì độ dài của vectơ ![]() là
là ![]()
từ đó nếu các điểm A1; A2 theo thức tự biểu diễn các số phức z1; z2 thì ![]()
b) Với mọi số phức z, z’ ta có |zz'| = |z||z'| và khi z ≠ 0 thì ![]()
c) Với mọi số phức z, z’ ta có |z + z'| ≤ |z| + |z'|.
Lời giải:
a)
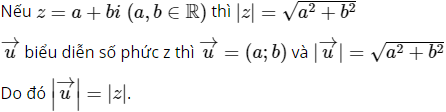
Gọi A1 là điểm biểu diễn số phức z1 = a1 + b1i ⇒ A1 (a1; b1)
A2 là điểm biểu diễn số phức z2 = a2 + b2i ⇒ A2 (a2; b2)
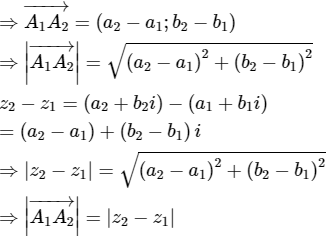
b) z = a + bi; z′ = a′ + b′i thì |z|2 = a2 + b2; |z′|2 = a′2+b′2 và
z.z′ = (aa′ − bb′) + (ab′ + a′b)i nên
|z.z′|2 = (aa′ − bb′)2 + (ab′ + a′b)2
= (aa′) + (bb′)2 − 2aa′bb′ + (ab′)2 + (a′b)2 + 2ab′a′b
= (aa′)2 + (bb′)2 + (ab′)2 + (a′b)2
|z|2.|z′|2 = (a2 + b2)(a′2 + b′2)
= a2a′2 + a2b′2 + a′2b2 + b2b′2
= (aa′)2 + (bb′)2 + (ab′)2 + (a′b)2
⇒ |zz′|2 = |z|2.|z′|2
⇒ |zz′| = |z|.|z′|
Khi z ≠ 0 ta có:
c) Với mọi số phức z, z’, ta có: z + z’ = (a +a’) + (b +b’)i
⇒ |z + z′| = √[(a + a′)2 + (b + b′)2]
|z| + |z′| = √(a2 + b2) +√(a′2 + b′2)
Theo yêu cầu bài toán ta cần chứng minh:
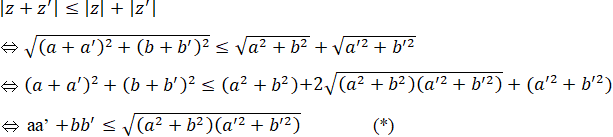
Theo Bu-nhi-cốp-xki ta có bất đẳng thức (*) đúng với ∀a,b,a',b' ∈ R nên |z+z'| ≤ |z|+|z'| (đpcm).
Cách khác:
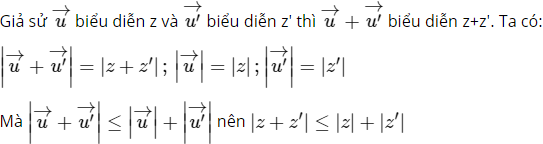
Dấu "=" xảy ra khi z = 0 hoặc z′ = 0.
Bài 9 trang 190 SGK
Xác định tập hợp câc điểm reong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau:
![]()
Lời giải:
a) Giả sử z = x + yi, x,y ∈ R
Khi đó z − i = x+ (y − 1)i
|z − i| = 1 ⇔ x2 + (y − 1)2 = 1.
Tập hợp các điểm M biểu diễn số phức z là đường tròn tâm I(0,1) bán kính 1.
b) Giả sử z = x + yi, x,y ∈ R.
Ta có:
![]()
⇔ x2 + (y − 1)2 = x2 + (y + 1)2
⇔ x2 + y2 − 2y + 1 = x2 + y2 + 2y + 1
⇔ y = 0
⇔ z là số thực.
Tập hợp M là trục thực Ox.
c) Giả sử z = x + yi, x,y ∈ R.
⇔ |x + yi| = |x − yi − 3 + 4i|
⇔ |x + yi| = |(x − 3) + (4 − y)i|
⇔ x2 + y2 = (x − 3)2 + (4 − y)2
⇔ 6x + 8y = 25
Tập hợp M là đường thẳng có phương trình: 6x + 8y = 25.
Luyện tập
Bài 10 trang 190 SGK
Chứng minh rằng với mọi số phức z ≠ 1, ta có:
![]()
Lời giải:
Vì z ≠ 1, nên tính chất của số phức ta có đẳng thức cần chứng minh tương đương với:
(1 + z + z2 + ⋯ + z9 )(z − 1) = z10 − 1
⇔ z + z2 + z3 +⋯ + z10 − 1 − z − z2 − z3 −… −z9 = z10 − 1
⇔ z10 − 1 = z10 − 1 (đpcm)
Vậy ta có điều cần chứng minh.
Bài 11 trang 191 SGK
Hỏi mỗi số sau đây là số thực hay số ảo (z là số phức tùy ý cho trước sao cho biểu thức xác định)?
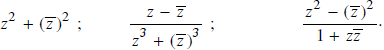
Lời giải:
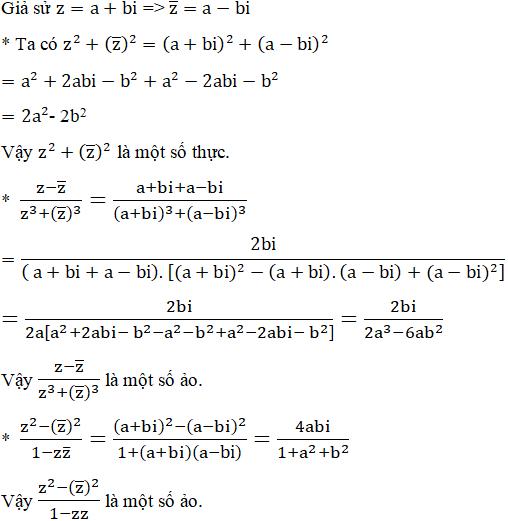
Bài 12 trang 191 SGK
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thõa mãn từng điền kiện sau:

Lời giải:
a) Ta có: z2 = (a + bi)2 = (a2 − b2 ) + 2abi
Vì z2 là số thực âm nên
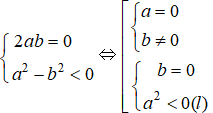
Vậy các điểm cần tìm là trục ảo trừ đi điểm gốc O (0; 0).
b) z2 = (a2 − b2) + 2abi là số ảo khi a2 − b2 = 0 ⇔ a = ±b
Vậy tập hợp các điểm là hai đường phân giác của góc tạo bởi trục thực và trục ảo.
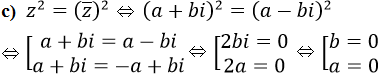
Vậy tập hợp các điểm cần tìm là hợp của trục thực và trục ảo.
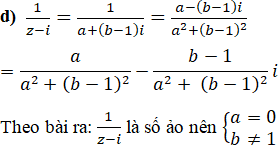
Vậy tập hợp các điểm là trục ảo bỏ đi điểm I(0; 1) biểu diễn số i.
Bài 13 trang 191 SGK
Tìm nghiệm phức của các phương trình sau:
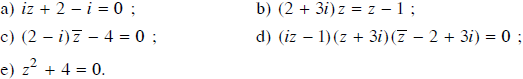
Lời giải:
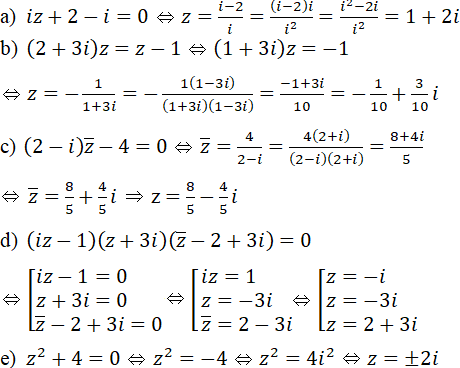
Bài 14 trang 191 SGK
a) Cho số phức z = x + yi (x,y ∈ R). Khi z ≠ 1, hãy tìm phần thực và phần ảo của số phức ![]() .
.
b) Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện
![]()
là số thực dương.
Lời giải:
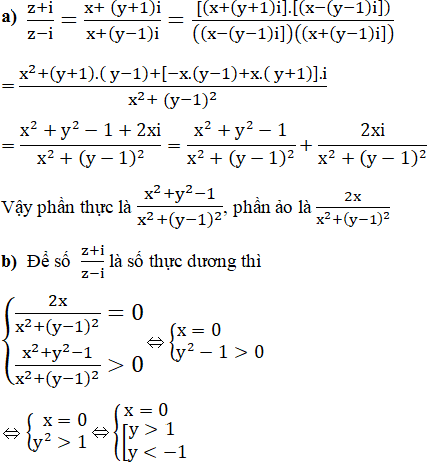
Vậy quỹ tích điểm cần tìm là trục ảo bỏ đi đoạn IJ, trong đó I(0; 1); J(0; -1).
Bài 15 trang 191 SGK
a) Trong mặt phẳng phức, cho ba điểm A, B, C không thẳng hàng theo thứ tự biểu diễn các số phức z1; z2; z3. Hỏi trọng tâm của tam giác ABC biểu diễn số phức nào?
b) Xét ba điểm A, B, C của mặt phẳng phức theo thứ tự biểu diễn ba số phức phân biệt z1; z2; z3 thõa mãn |z1| = |z2| = |z3|.
Chứng minh rằng A, B, C là ba đỉnh của một tam giác đều khi và chỉ khi z1 + z2 + z3 = 0.
Lời giải:
Giả sử z1 = a1 + b1 i ⇒ A(a1; b1)
z2 = a2+b2 i ⇒ B(a2; b2)
z3 = a3 + b3 i ⇒ C (a3; b3)
a) Suy ra trọng tâm G của tam giác ABC là ![]()
là điểm biểu diễn số phức: ![]()
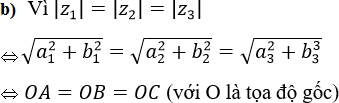
Vậy O là tâm đường tròn ngoại tiếp ΔABC. Để ΔABC là Δ đều thì O cũng là trọng tâm của ΔABC
Theo câu a) trọng tâm tam giác ABC là
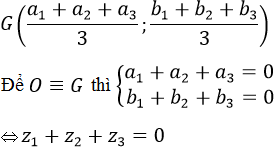
Bài 16 trang 191 SGK
Đố vui. Trong mặt phẳng phức cho các điểm: O gốc tọa độ, A biểu diễn số 1, B biểu diễn số phức z không thực, A’ biểu diễn số phức z' ≠ 0 và B’ biểu diễn số phức zz’.
Hai tam giác OAB.OA’B’ có phải là tam giác đồng dạng không?
Lời giải:
Gọi z = a + bi (ab ≠ 0) z'= a' + b' i(a' b' ≠ 0)
Suy ra zz’ = (aa’ – bb’) (a’b +b’a)i
Ta có:
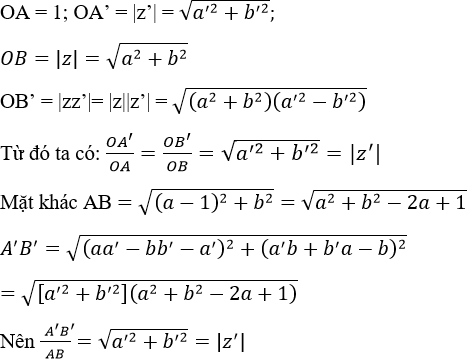
Vậy ta có:
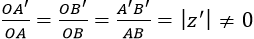
nên tam giác OAB đồng dạng với tam giác OA’B’.



































