Câu hỏi và bài tập
Bài 12 trang 81 SGK
Xét mệnh đề: “Với các số thực a, b, x nếu 0 < a < b thì ax < bx."
Với điều kiện nào sau đây của x thì mệnh đề đúng?
A. x bất kì B. x > 0 C. x < 0
Lời giải:
Điều kiện B, vì theo tính chất của lũy thừa với số mũ thực.
Bài 13 trang 81 SGK
Xét mệnh đề: “Với các số thực a, x, y nếu x < y thì ax < ay."
Với điều kiện nào sau đây của a thì mệnh đề đó đúng?
A. a bất kì B. a > 0 C. a > 1
Lời giải:
Điều kiện C, vì theo tính chất của lũy thừa với số mũ thực.
Bài 14 trang 81 SGK
Cho các số thực a, x, y với x < y. Tìm điều kiện của a để ax > ay.
Lời giải:
Theo tính chất lũy thừa với số mũ thực thì điều kiện của a là: 0 < a < 1.
Bài 15 trang 81 SGK
Tính các biểu thức
![]()
Lời giải:
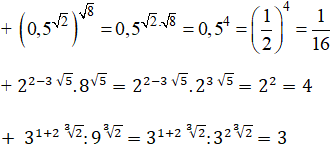
Bài 16 trang 81 SGK
Đơn giản các biểu thức
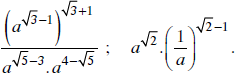
Lời giải:
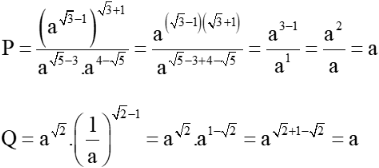
Bài 17 trang 81 SGK
Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi xuất 7, 56% một năm. Giả sử lãi xuất không thay đổi. Hỏi số tiền lãi người đó thu được (cả vốn lẫn lãi) sau 5 năm là bao nhiêu triệu đồng?
Lời giải:
Áp dụng công thức lãi kép C = A(1 + r)N
Trong đó A =15, r = 7,56%, N = 5 ⇒ C = 15(1 + 7,56%)5 = 15.1,07565 ≈ 21,59 triệu đồng.
Luyện tập
Bài 18 trang 81 SGK
Viết các biểu thức sau dưới dạng lũy thừa của một số với số mũ hữi tỉ:
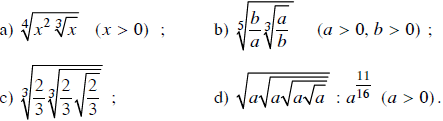
Lời giải:
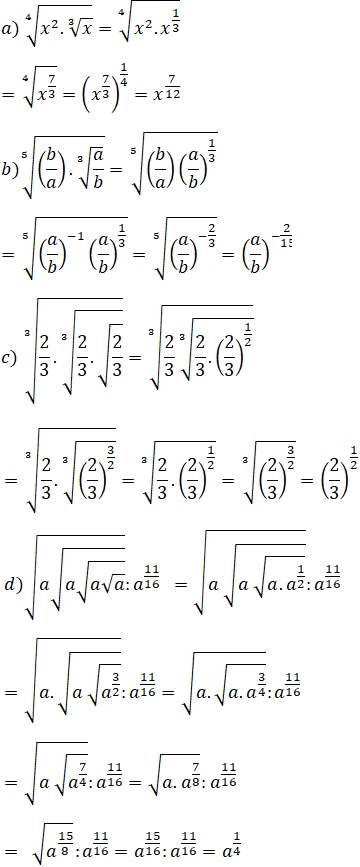
Bài 19 trang 82 SGK
Đơn giản biểu thức
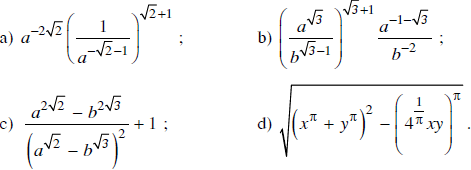
Lời giải:
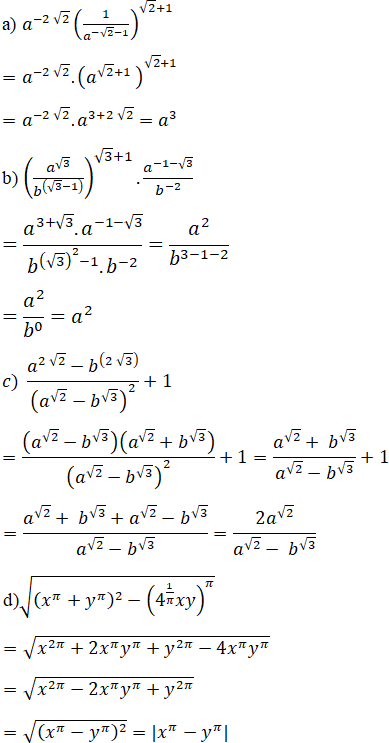
Bài 20 trang 82 SGK
Tìm số thực α, thỏa mãn từng điều kiện sau:
![]()
Lời giải:
a) (aα + a(-α))/2 = 1
⇔ aα + a(-α) = 2
⇔ a2α – 2aα + 1 = 0
⇔ (aα – 1)2 = 0
⇔ aα – 1= 0
⇔ α = 0
b) 3|α| < 27 ⇔ 3|α| < 33 ⇔ |α| < 3 ⇔ -3 < α < 3 (vì 3 > 1)
Bài 21 trang 82 SGK
Giải các phương trình sau bằng cách đặt t = ∜x :
a) √x + ∜x = 2; b) √x - 3∜x + 2 = 0.
Lời giải:
a) Đặt t = ∜x (t > 0) ta được:
t2 + t – 2 = 0 ⇔ t = 1 hoặc t = -2 (loại)
Với t = 1 ⇒ 1 = ∜x ⇔ x = 1
b) Đặt t = ∜x ta được:
t2 – 3t + 2 = 0 ⇔ t = 1 hoặc t = 2
Với t = 1 ⇔ 1 = ∜x ⇔ x = 1
Với t= 2 ⇔ 2 = ∜x ⇔ x = 16
Bài 22 trang 82 SGK
Giải các bất phương trình sau:
a) x4 < 3; b) x11 ≥ 7; c) x10 > 2; d) x3 ≤ 5.
Lời giải:
a) x4 < 3 ⇔ |x| < ∜3 ⇔ -∜ 3 < x < ∜3
Tập nghiệm S = (-∜ 3; ∜3)
b) x11 ≥ 7 ⇔ x ≥ 11√7
Vậy S = [11√7; +∞)
c) x10 > 2;
⇔ |x| > 10√2 ⇔ x < −10√2 hoặc x > 10√2.
Vậy S = (−∞; −10√2) ∪ (10√2; +∞)
d) x3 ≤ 5 ⇔ x ≤ ∛5
Vậy S = (−∞; ∛5).



































