Câu hỏi và bài tập
Bài 16 trang 22 SGK
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f(x) = sin4x + cos4x.
Lời giải:
Hàm số xác định trên R.
Ta có: f(x) = (sin2x)2 + (cos2x)2
= (sin2x + cos2x)2 – 2sin2x.cos2x
= 1 – 1/2 sin22x với x ∈ R.
f(x) ≤ 1, ∀x ∈ R, f(0) = 1.
Vậy maxx ∈ R f(x) = 1
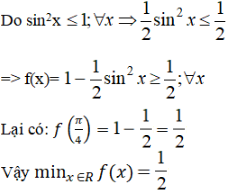
Bài 17 trang 22 SGK
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
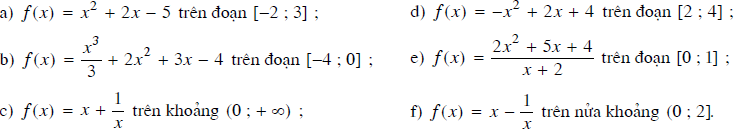
Lời giải:
a. Hàm số f(x)= x2 + 2x – 5
Tập xác định D = R.
Đạo hàm y’= 2x +2 = 0 ⇔ x = -1
Cách 1. Bảng biến thiên:
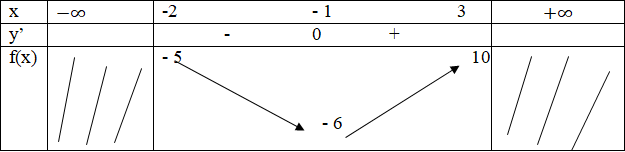
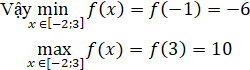
Cách 2. Ta có: f(-2) = -5; f(-1) = -6; f(3) = 10
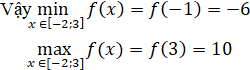
b. Hàm số ![]()
Hàm số đã cho xác định trên R
f'(x) = x2 + 4x + 3; f'(x) = 0 ⇔ x = -1 hoặc x = -3
Ta có: f(-4) = -16/3; f(-3) = -4; f(-1) = -16/3; f(0) = -4
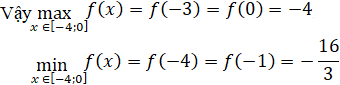
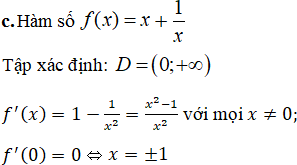
Bảng biến thiên:
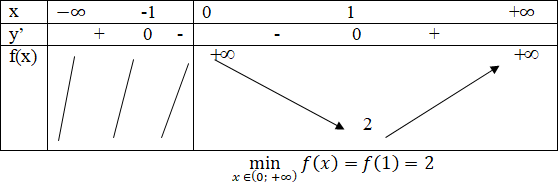
Hàm số không đạt giá trị lớn nhất trên (0; +∞)
d. Hàm số y = -x2 +2x + 4
Hàm số liên tục trên R.
f' (x)= -2x + 2; f'(x) = 0 ⇔ x = 1 (loại vì x = 1 không thuộc [2; 4])
Ta có: f(2) = 4; f(4) = -4
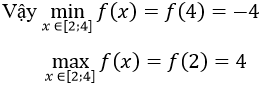
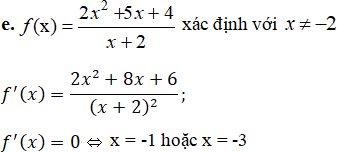
Cách 1. Bảng biến thiên:
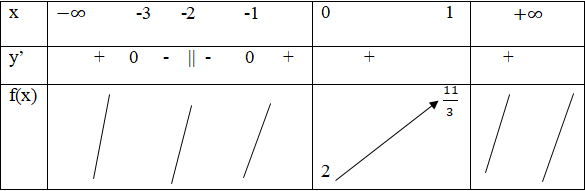
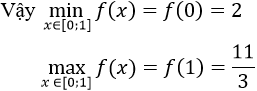
Cách 2. Vì x ∈ [0; 1] nên Phương trình f’(x) = 0 vô nghiệm trên [0; 1]
Ta có: f(0) = 2; f(1) = 11/3
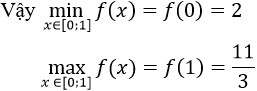
f(x)= x – ![]()
f'(x) = 1 + ![]() > 0, ∀x ∈ (0; 2)
> 0, ∀x ∈ (0; 2)
f(x) liên tục trên (0; 2] nên f(x) đồng biến trên (0; 2]
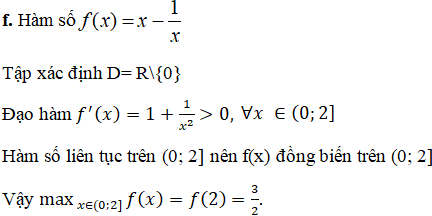
Hàm số không đạt giá trị nhỏ nhất trên nửa khoảng (0; 2].
Bài 18 trang 22 SGK
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = 2 sin2x + 2sinx – 1
b) y = cos2x – sinxcosx + 4
Lời giải:
a. Đặt t = sin x, -1 ≤ t ≤ 1. Khi đó, hàm số đã cho trở thành:
y = f(t) = 2t2 + 2t – 1, t ∈ [-1; 1]
Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của y = f(t) trên [-1;1]. Đó là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên R
f'(t) = 4t + 2, f'(t) = 0 ⇔ t = -1/2
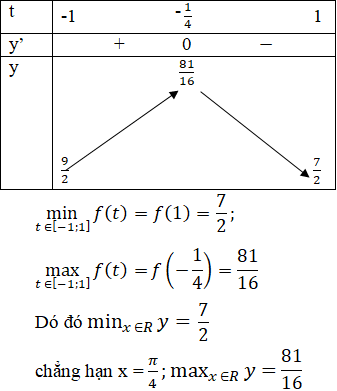
Bảng biến thiên:
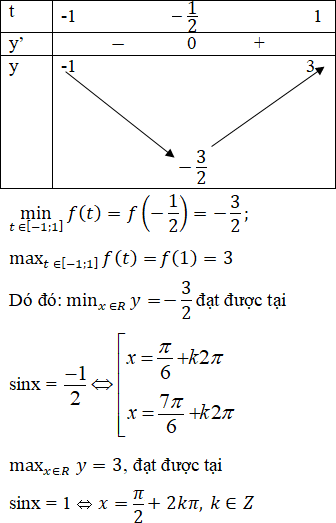
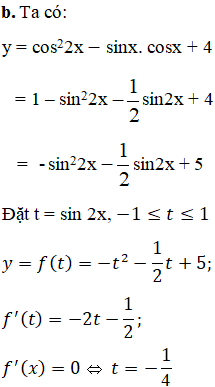
Bảng biến thiên:
Bài 19 trang 22 SGK
Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trí của điểm M sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.
Lời giải:
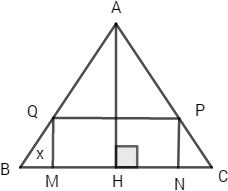
Đặt BM = x (0 < x < a/2)
Ta có: MN = a – 2x; QM = BM.tan B = x √3
Diện tích hình chữ nhật MNPQ là:
S(x) = QM.MN = x√3(a –2x)
S(x) = √3(ax – 2x2)
Bài toán trở thành tìm giá trị lớn nhất của S(x) trên khoảng (0; a/2)
Ta có S'(x) = √3(a – 4x); S'(x) = 0 ⇔ x = a/4
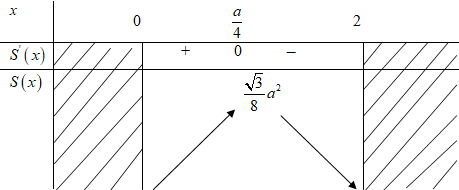
S đạt giá trị lớn nhất tại x = a/4 và giá trị lớn nhất của diện tích hình chữ nhât MNQP là:
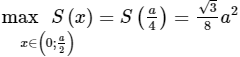
Bài 20 trang 22 SGK
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng
P(n) = 480 – 20n (gam)
Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Lời giải:
Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ, số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân nặng:
f(n) = n.P(n) = 480n – 20n2, n ∈ N*
Xét hàm số f(x) = 480x – 20x2 trên khoảng (0; +∞)
(Biến n lấy các giá trị nguyên dương được thay bằng biến số x lấy các giá trị trên khoảng (0; +∞))
Ta có: f'(x) = 480 – 40x
f' (x) = 0 ⇔ x = 12
Bảng biến thiên
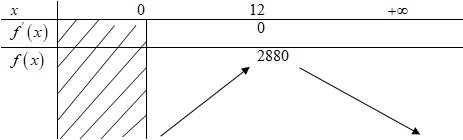
Trên (0; +∞) hàm số f(x) đạt giá trị lớn nhất tại x = 12
Suy ra trên tập hợp N* các số nguyên dương, hàm số f đạt giá trị lớn nhất tại điểm n = 12.
Vậy muốn thu hoạch được nhiều cá nhất sau một vụ thì trên mỗi đơn vị diện tích của mặt hồ phải thả 12 con cá.
Luyện tập
Bài 21 trang 22 SGK
Tìm cực trị của các hàm số sau:
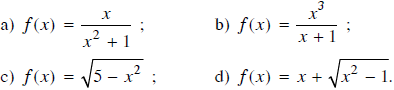
Lời giải:
a. Tập xác định: D = R.
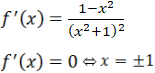
Bảng biến thiên
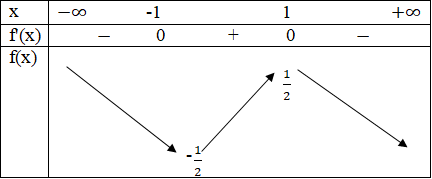
Hàm số đạt cực tiểu tại x = -1; fCT = f(-1) = -1/2
Hàm số đạt cực đại tại x = 1; fCĐ= f(1) = 1/2
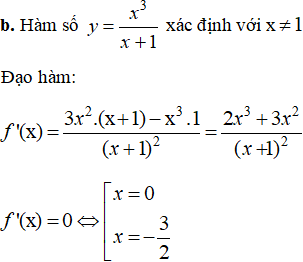
Bảng biến thiên
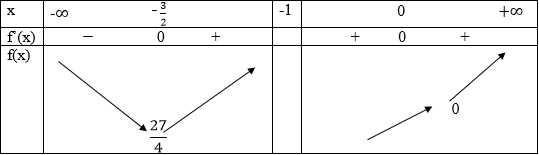
Vậy hàm số đạt cực tiểu tại điểm x=-3/2; f(-3/2) = 27/4
Hàm số không có cực đại.
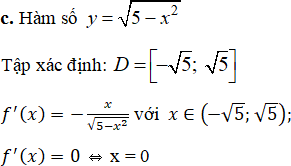
Bảng biến thiên
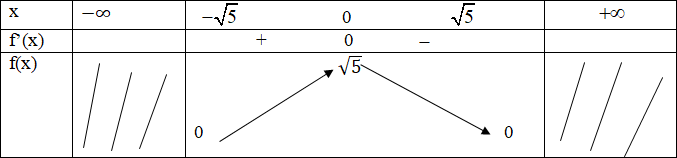
Hàm số đạt cực đại tại điểm x = 0; fCĐ = f(0) = √5
Hàm số không có cực tiểu.
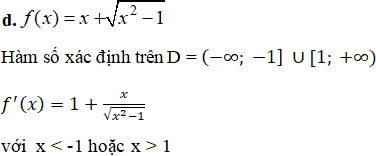
Bảng biến thiên
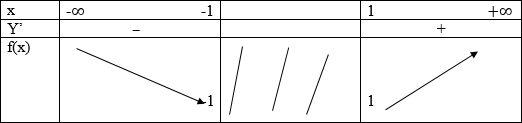
Hàm số nghịch biến trên (- ∞; -1] và đồng biến trên [1; +∞)
Hàm số không có cực trị.
Bài 22 trang 23 SGK
Tìm giá trị của m để hàm số có cực đại và cực tiểu.
![]()
Lời giải:
Tập xác định: D = R\{1}
Đạo hàm:
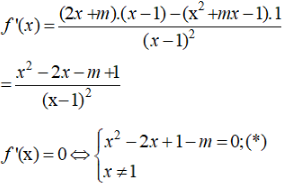
Phương trình (*) có nghiệm x ≠ 1 khi và chỉ khi:
12 – 2.1 + 1 – m ≠ 0 hay m ≠ 0
Hàm số có cực đại và cực tiểu khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 1, nghĩa là:
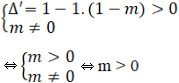
Vậy f(x) có cực đại và cực tiểu khi và chỉ khi m > 0
Bài 23 trang 23 SGK
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức
G(x) = 0,025x2 (30 – x)
trong đó x là liếu lượng thuốc được tiêm cho bệnh nhận (x lấy đơn vị là miligam). Tính liều lượng thuộc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm đó.
Lời giải:
Ta có G(x) = 0,75x2 – 0,025x3;
G' (x) = 1,5x – 0,075x2;
G(x)' = 0 ⇔ x = 0 hoặc x = 20
Bảng biến thiên.
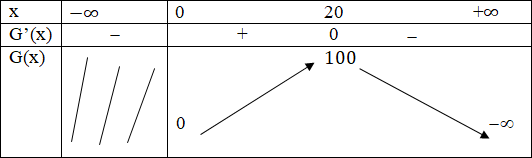
maxx > 0G(x) = G(20) = 100
Vậy liều lượng cần tiêm cho bệnh nhân huyết áp giảm nhiều nhất là 20mg.
Khi đó, độ giảm huyết áp là 100
Vậy liều lượng cần tiêm cho bệnh nhân huyết áp giảm nhiều nhất là 20mg. khi đó, độ giảm huyết áp là 100.
Bài 24 trang 23 SGK
Cho parabol (P): y = x2 và điểm A (-3; 0). Xác định điểm M thuộc parabol (P) sao cho khoảng cách AM là ngắn nhất và tìm khoảng cách ngắn nhất đó.
Lời giải:
Gọi M(x; x2) là một điểm bất kì trên (P).
Ta có: AM2 = (x + 3)2 +(x2)2 = x4 + x2 + 6x + 9
AM nhỏ nhất ⇔ f(x) = x4 + x2 + 6x + 9 đạt giá trị nhỏ nhất.
f'(x) = 4x3 + 2x + 6 = (x + 1)(4x2 – 4x + 6)
f'(x) = 0 ⇔ x = -1
Bảng biến thiên
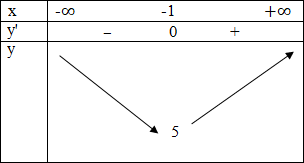
Dựa vào bảng biến thiên suy ra, hàm số đạt nhỏ nhất tại điểm x = -1; f(-1) = 5.
Suy ra, khoảng cách AM đạt giá trị nhỏ nhất khi tọa độ điểm M (-1; 1). Lúc đó AM = √5
Bài 25 trang 23 SGK
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của con cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của con cá trong t giờ được cho bởi công thức
E(v) = cv3t
trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Lời giải:
Vận tốc của các khi bởi ngược dòng nước là v – 6 (km/h). thời gian cá bơi để vượt qua một khoảng cách 300 km là: ![]()
Năng lượng tiêu hao của cá để vượt khoảng cách đó là:
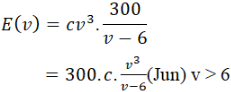
Bài toán trở thành tìm v > 6 để E(v) nhỏ nhất.
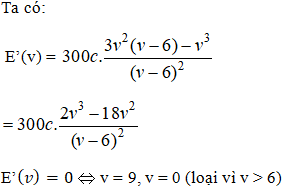
Bảng biến thiên
Vậy tiêu hao ít năng lượng nhất, cá phải bởi với vận tốc 9 km/h (khi nước đứng yên).
Bài 26 trang 23 SGK
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là
f(t) = 45t2 – t3; t = 0; 1; 2; 3…; 25.
Nếu coi f là hàm số xác định trên đoạn [0; 25] thì f'(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t.
a) Tính tốc độ truyền bệnh vào ngày thứ 5.
b) Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó.
c) Xác định các ngày mà tốc độ truyền bệnh lớn hơn 600.
d) Xét chiều biến thiên của hàm số f trên đoạn [0; 25].
Lời giải:
Số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 45t2 – t3, t nguyên thuộc đoạn [0; 25]
Để xét tốc độ truyền bệnh, xem f(t) là hàm số xác định trên đoạn [0; 25]
a. f' (t) = 90t – 3t2 = 3t(30 – t)
Tốc độ truyền bệnh vào ngày thứ 5 là: f’(t) = 375 người/ngày
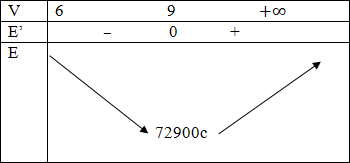
b. Bài toán trờ thành: tìm t ∈ [0; 25] để f’(t) là lớn nhất.
Ta có: f’’(t) = 90 – 6t; f’’(t) = 0 ⇔ t = 15
Bảng biến thiên:
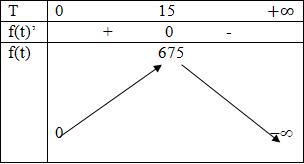
Vậy tốc độ truyền bệnh lớn nhất là vào ngày thứ 15.
Tốc độ đó là f’(15) = 675 người/ngày
c. Để f’(t) > 600 ⇔ 90t – 3t2 > 600 ⇔ 10 < t < 20
Từ ngày thứ 11 đến ngày thứ 19, tốc độ truyền bệnh là lớn hơn 600 người mỗi ngày.
d. f(t) liên tục trên [0; 25]
Do f’(t) = 3t(30 – t) > 0 với ∀ t ∈ (0; 25)
⇒ f(t) đồng biến trên [0; 25]
Bài 27 trang 24 SGK
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
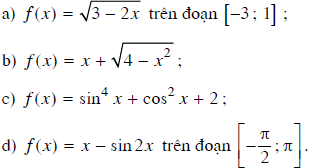
Lời giải:


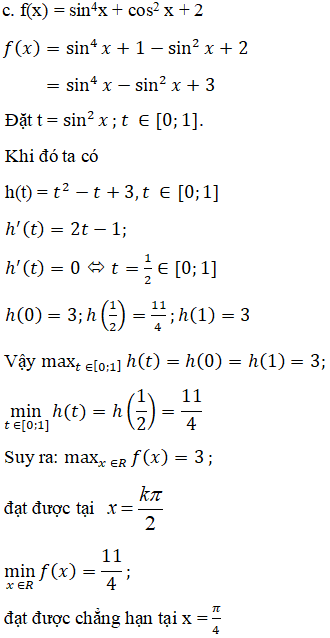
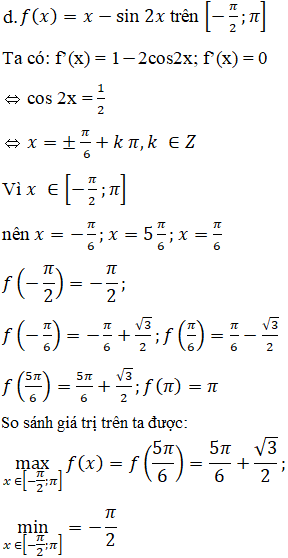
Bài 28 trang 24 SGK
Trong các hình chữ nhật có chu vi là 40cm, hãy xác định hình chữ nhật có diện tích lớn nhất.
Lời giải:
Cách 1. Vì chu vi của hình chữ nhật là 40 cm nên kích thước là x, 20 – x (cm) (0 < x <20)
Diện tích hình chữ nhậ trên là:
S(x) = x(20 – x) = 20x – x2 x ∈ (0; 20)
S'(x) = 20 – 2x; S' (x) = 0 ⇔ x = 10
Bảng biến thiên:
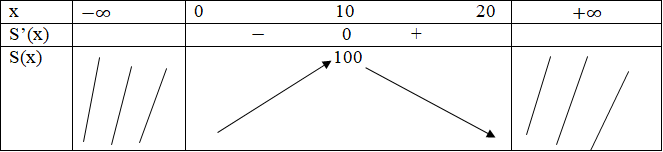
Vậy trong tất cả các hình chữ nhật có chu vi 40 cm, hình vuông có cạnh là 10 cm có diện tích lớn nhất.
Cách 2.
| Hướng dẫn: Sử dụng bất đẳng thức cô - si. Hai số dương a, b có tổng không đổi thì tích của chúng là lớn nhất khi và chỉ khi a = b |
Gọi a, b là hai cạnh của hình chữ nhật, ta có a + b = 20 (a, b >0
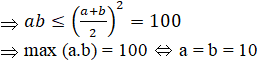
Vậy hình vuông có cạnh 10 cm là diện tích lớn nhất (trong tất cả các hình chữ nhật có chu vi 40 cm)