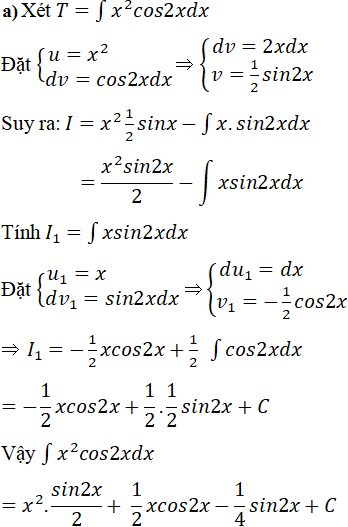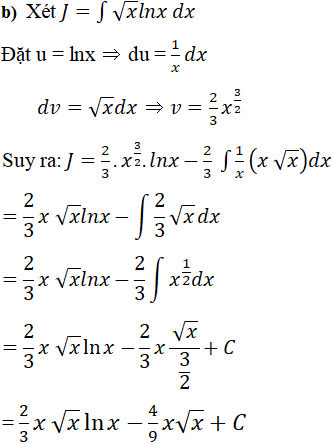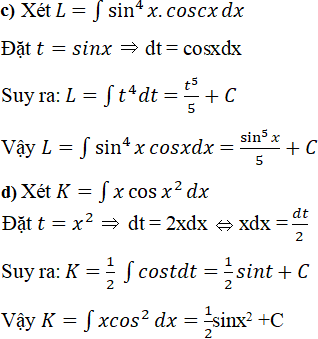Câu hỏi và bài tập
Bài 5 Trang 145 SGK
Dùng phương pháp đổi biến số, tìm nguyên hàm của các hàm số sau:
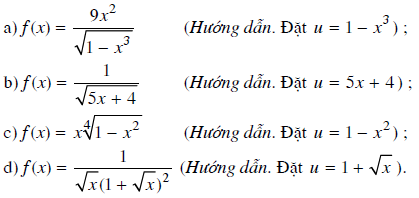
Lời giải:
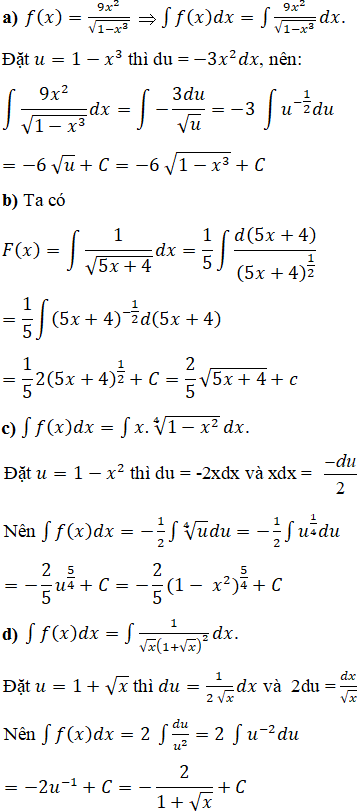
Bài 6 Trang 145 SGK
Dùng phương pháp lấy nguyên hàm từng phần, tìm nguyên hàm các hàm số sau:
a) f(x) = xsin(x/2) b) f(x) = x2 cosx
c) f(x) = x.ex d) f(x) = x3 ln(2x)
Lời giải:
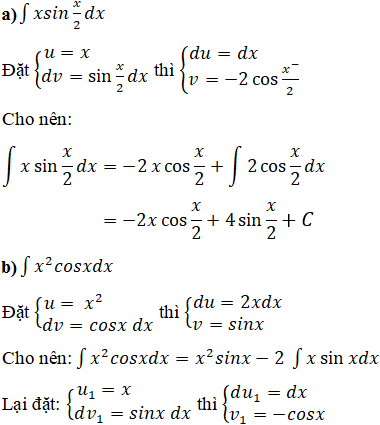
Cho nên: ∫x2 cosxdx = x2 sinx – 2[–xcosx + ∫cosxdx] = x2 sinx + 2xcosx – 2sinx + C
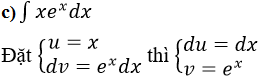
Cho nên: ∫xex dx = xex – ∫ex dx = xex – ex + C
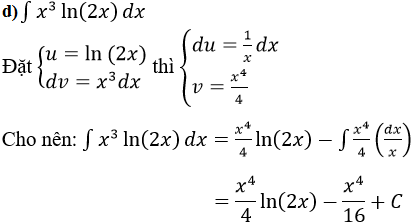
Luyện tập
Tìm nguyên hàm của các hàm số sau:
Bài 7 Trang 145 SGK
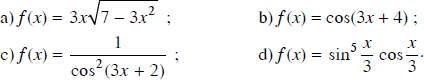
Lời giải:
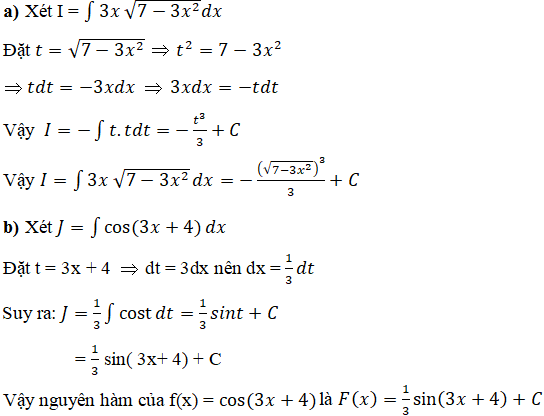
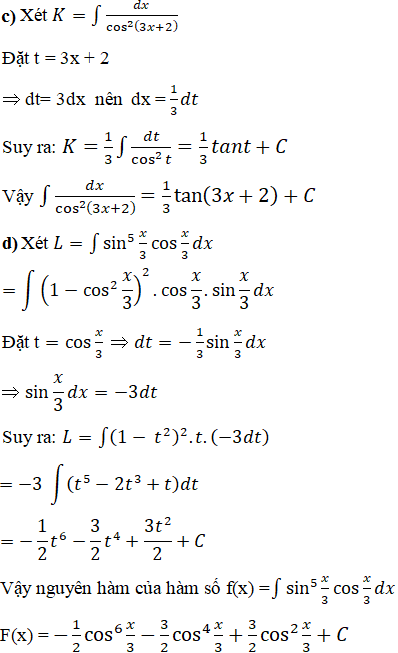
Bài 8 Trang 145 SGK

Lời giải:
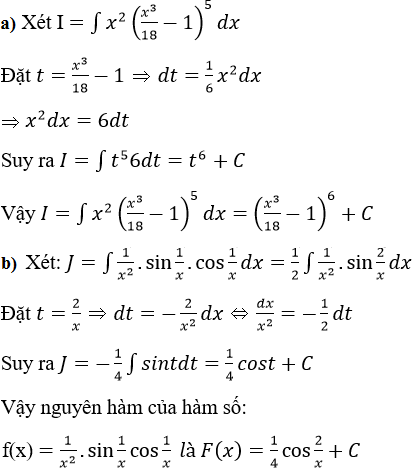
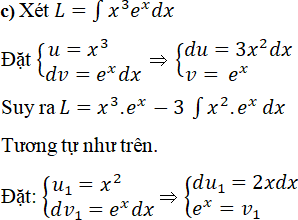
⇒ L = x3.ex – 3(x2.ex ) + 6∫xex dx = x3.ex – 3x2.ex + 6xex – 6ex + C
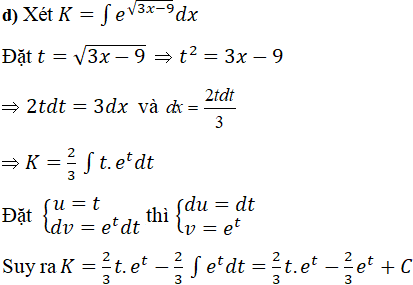
Bài 9 Trang 146 SGK
a) f(x) = x2 cos 2x; b) f(x) = √x lnx;
c) f(x) = sin4 x.cos x; d) f(x) = x cos(x2).
Lời giải: