Bài giải GIẢI TÍCH 12 - ÔN TẬP CUỐI NĂM | Sách Bài Giải

Câu hỏi

Câu 1 trang 145 SGK

Định nghĩa sự đơn điệu ( đồng biến, nghịch biến) của một hàm số trên một khoảng.

Lời giải:

Cho hàm số y = f(x) xác định trên khoảng K, hàm số f(x) được gọi là

+ Đồng biến trên K nếu ∀ x₁, x₂ ∈ K thỏa mãn x₁ < x₂ thì f(x₁) < f(x₂).

+ Nghịch biến trên K nếu ∀ x₁, x₂ ∈ K thỏa mãn x₁ < x₂ thì f(x₁) > f(x₂)

Hàm số chỉ đồng biến hoặc nghịch biến trên K gọi là đơn điệu trên K.

Câu 2 trang 145 SGK

Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.

Lời giải:

Cho hàm số y = f(x) có đạo hàm trên K.

+ f(x) đồng biến trên K ⇔ f’(x) ≥ 0 với ∀ x ∈ K, f’(x) = 0 tại hữu hạn điểm.

+ f(x) nghịch biến trên K ⇔ f’(x) ≤ 0 với ∀ x ∈ K, f’(x) = 0 tại hữu hạn điểm.

Câu 3 trang 145 SGK

Phát biểu các điều kiện đủ để hàm số f(x) có cực trị ( cực đại cực tiểu) tại điểm x_o.

Lời giải:

Điều kiện để hàm có cực trị:

Định lí 1: Cho hàm số y = f(x) liên tục trên K = (x_o – h; x_o + h), h > 0 và có đạo hàm trên K hoặc trên K \ {x_o}, nếu:

- f’(x) > 0 trên (x_o – h; x_o) và f’(x) < 0 trên (x_o; x_o + h) thì x0 là một điểm cực đại của f(x).

- f’(x) < 0 trên (x_o – h; x_o) và f’(x) > 0 trên (x_o; x_o + h) thì x0 là một điểm cực tiểu của f(x).

Câu 4 trang 145 SGK

Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số.

Lời giải:

Bước 1: Tìm tập xác định của hàm số

Bước 2: Xét sự biến thiên

- Xét chiều biến thiên:

+ Tìm đạo hàm f’(x)

+ Tìm các điểm mà tại đó f’(x) bằng không hoặc không xác định

+ Xét dấu của đạo hàm f’(x) và suy ra chiều biến thiên của hàm số.

- Tìm cực trị

- Tìm giới hạn vô cực và tiệm cận ( nếu có)

- Lập bảng biến thiên.

Bước 3: Vẽ đồ thị hàm số.

Câu 5 trang 145 SGK

Nêu định nghĩa và các tính chất cơ bản của lôgarit.

Lời giải:

+ Định nghĩa của lôgarit: Cho hai số dương a; b sao cho a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là lôgarit cơ số a của b và kí hiệu: log_ab.

+ Các tính chất cơ bản của lôgarit:

Cho a > 0; b > 0 và a ≠ 1 ta có:

log_a1 = 0; log_aa = 1

a^log_ab = b;

log_a(a^α) = α.

Câu 6 trang 145 SGK

Phát biểu định lí về quy tắc logarit, công thức đổi cơ số.

Lời giải:

Quy tắc tính logarit

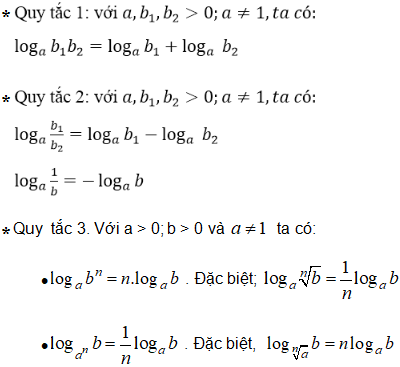
Đổi cơ số

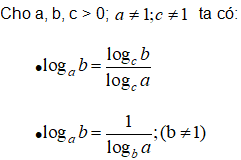
Câu 7 trang 145 SGK

Nêu tính chất của hàm số mũ, hàm số logarit, mối liên hệ giữa đồ thị của hàm số mũ cà hàm số logarit cùng cơ số.

Lời giải:

1. Hàm số mũ

Cho số a > 0 và a ≠ 1. Hàm số y = a^x được gọi là hàm số mũ cơ số a.

Các tính chất của hàm số mũ y = a^x

Tập xác định	(-∞; +∞)
Đạo hàm	y’= ax.lna
Chiều biến thiên	+ Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến
Tiệm cận	Trục Ox là tiệm cận ngang
Đồ thị	Đi qua các điểm (0; 1); (1; a)
	Nằm phía trên trục hoành (y = ax > 0 mọi x)

2. Hàm Logarit

Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a

Tập xác định	(0; +∞)
Đạo hàm
Chiều biến thiên	+ Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1; 0); (a; 1)
	Nằm bên phải trục tung.

3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.

Câu 8 trang 145 SGK

Nêu định nghĩa và các phương pháp tính nguyên hàm.

Lời giải:

+ Định nghĩa nguyên hàm:

Cho hàm số f(x) xác định trên K (K là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.

+ Phương pháp tính nguyên hàm

* Đổi biến số:

Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số liên tục, có đạo hàm thì:

∫f(u(x)). u'(x)dx = F(u(x)) + C

+ Phương pháp nguyên hàm từng phần:

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì

∫u(x). v'(x)dx = u(x). v(x) − ∫v(x). u'(x)dx

Hay ∫udv = uv − ∫vdu

Câu 9 trang 145 SGK

Nêu định nghĩa và các phương pháp tính tích phân.

Lời giải:

• Định nghĩa

Cho hàm số y = f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)

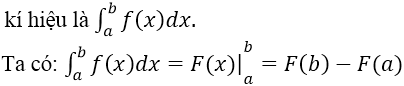
• Phương pháp tính tích phân

a) Đổi biến số:

Định lí 1: Cho hàm số f(x) liên tục trên [a; b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [ α; β] sao cho φ(α) = a; φ(β) = βvà a ≤ φ(t) ≤ b với mọi t ∈ [α; β]. Khi đó:

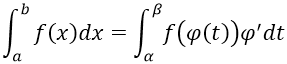
b) Tích phân từng phần

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

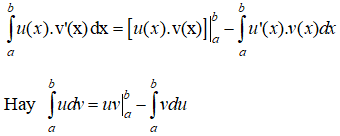
Câu 10 trang 145 SGK

Nhắc lại định nghĩa số phức, số phức liên hợp, mô đun của số phức. Biểu diễn hình học của số phức.

Lời giải:

1. Số phức

Mỗi biểu thức dạng a + bi, trong đó: a, b ∈ R;  i2= -1 được gọi là số phức. Trong đó a được gọi là phần thực, b gọi là phần ảo, số i là đơn vị ảo.

2. Mô đun

Cho số phức z = a + bi, được biểu diễn bởi điểm M(a;b) trên tọa độ Oxy. Ta gọi mô đun của số phức z, kí hiệu là |z| là đọ dài của vectơ OM.

3. Số phức liên hợp

Cho số phức z = a + bi, ta gọi a – bi là số phức liên hợp của z

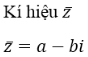
Bài tập

Bài 1 trang 145 SGK

 Cho hàm số f(x) = ax² – 2(a+1)x + a + 2 (a ≠ 0)

a) Chứng tỏ rằng phương trình f(x)=0 luôn có nghiệm thực. Tính các nghiệm đó.

b) Tính tổng S và tích P của các nghiệm của phương trình f(x) = 0. Khảo sát sự biến thiên và vẽ đồ thị của S và P theo a.

Lời giải:

Bảng biến thiên:

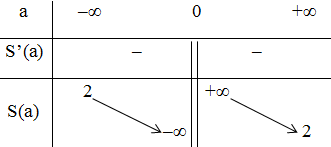
Đồ thị (hình thang trên).

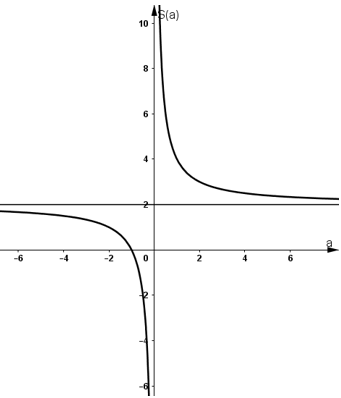
* Khảo sát hàm số

+ Tập xác định: D = R\{0}.

⇒ Đường thẳng a = 0 là tiệm cận đứng của đồ thị hàm số.

+ Lại có: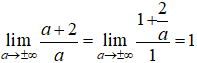

Do đó, đường thẳng P(a) =1 là tiệm cận ngang của đồ thị hàm số.

Do đó hàm số này nghịch biến trên tập xác định.

Bảng biến thiên

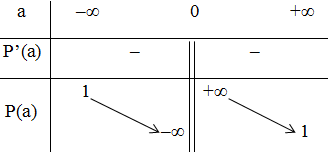
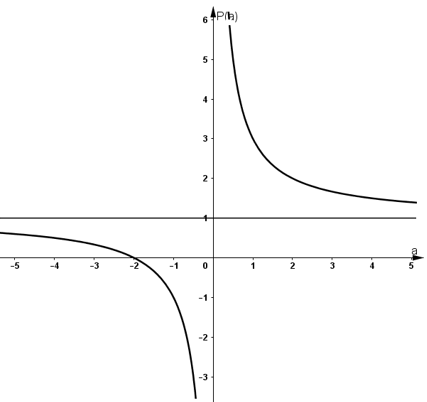
Đồ thị hàm số

Bài 2 trang 145 SGK

Cho hàm số:

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi a = 0.

b) Tính diện tích hình phẳng giới hạn bởi (C) và các đường thẳng y = 0; x = -1; x = 1.

Lời giải:

a) Với a = 0 ta có hàm số

- Tập xác định: D = ℝ.

- Sự biến thiên:

y’ = -x² – 2x + 3;

y’ = 0 ⇔ x = -3 hoặc x = 1.

- Bảng biến thiên:

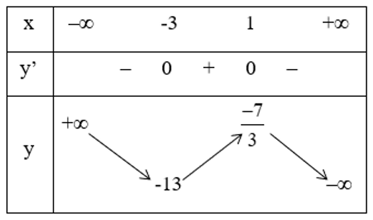
- Kết luận:

Hàm số đồng biến trên (-3; 1)

Hàm số nghịch biến trên (-∞; -3) và (1; +∞).

Hàm số đạt cực đại tại x = 1;

Hàm số đạt cực tiểu tại x = -3; y_CT = -13.

- Đồ thị hàm số:

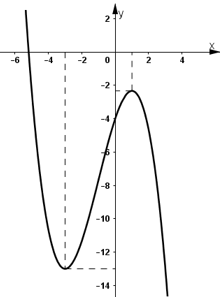
b) Hàm số đồng biến trên khoảng (-3; 1)

Nên y < y(1) = < 0, ∀ x ∈ (-1; 1).

Do đó, diện tích hình phẳng giới hạn bởi (C) và các đường thẳng y = 0; x = -1; x = 1 là:

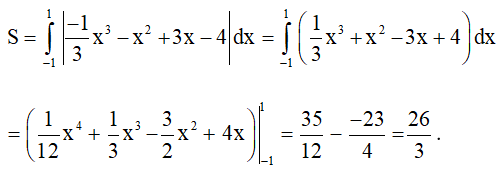
Bài 3 trang 146 SGK

Cho hàm số y = x³ + ax² + bx + 1

a) Tìm a và b để đồ thị của hàm số đi qua hai điểm: A(1; 2) và B(-2; -1).

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b.

c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 0, x = 0, x = 1 và đồ thị (C ) xung quanh trục hoành.

Lời giải:

a) Đồ thị hàm số đi qua A(1; 2) và B(-2; -1)

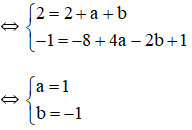
b) Với a = 1; b = -1, hàm số trở thành: y = x³ + x² – x + 1.

- Tập xác định: D = R.

- Sự biến thiên:

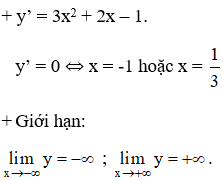
+ Bảng biến thiên:

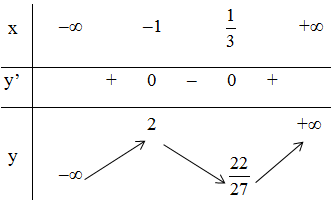
- Kết luận:

Hàm số đồng biến trên (-∞ ; -1) và

Hàm số nghịch biến trên

Hàm số đạt cực đại tại x = -1 ; y_CĐ = 2.

Hàm số đạt cực tiểu tại

- Đồ thị:

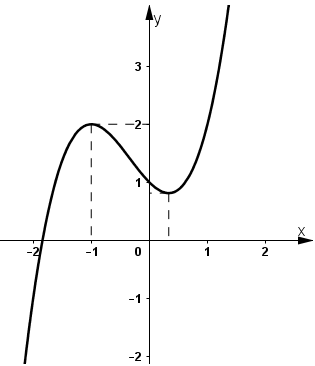
c) Thể tích vật cần tính là:

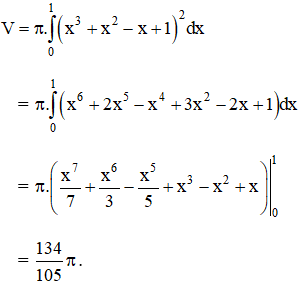
Bài 4 trang 146 SGK

Xét chuyển động thẳng được xác định bởi phương trình:

Trong đó t được tính bằng giây và S được tính bằng mét.

a) Tính v(2), a(2), biết v(t), a(t) lần lượt là vận tốc và gia tốc chuyển động đã cho.

b) Tìm thời điểm t mà tại đó vận tốc bằng 0.

Lời giải:

Theo ý nghĩa cơ học của đạo hàm ta có:

a) v(t) = s’(t) = t³ – 3t² + t – 3.

⇒ v(2) = 2³ – 3.2² + 2 – 3 = -5 (m/s)

a(t) = v’(t) = s’’(t) = 3t² – 6t + 1

⇒ a(2) = 3.2² – 6.2 + 1 = 1 (m/s²)

b) v(t) = 0

⇔ t³ – 3t² + t – 3 =0

⇔ (t – 3)(t² + 1) = 0

⇔ t = 3.

Vậy thời điểm t₀ = 3s thì vận tốc bằng 0.

Bài 5 trang 146 SGK

Cho hàm số y = x⁴ + ax² + b

a) Tính a, b để hàm số cực trị bằng 3/2 khi x = 1.

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi:

a = -1/2, b = 1

c) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.

Lời giải:

a) Đạo hàm y’ = 4x³ + 2ax

Hàm số có cực trị tại x = 1.

⇔ y’(1) = 0

⇔ 4.1³ + 2a.1 = 0

⇔ a = -2.

Lại có: y(1) = 3/2 nên:

1⁴ - 2.1² + b = 3/2

 ⇔ b = 5/2

Vậy a = -2; b = 5/2

b) Với ; b = 1 thì hàm số trở thành:

- TXĐ: D = R.

- Sự biến thiên:

y’ = 4x³ – x

y’ = 0 ⇔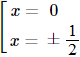 

+ Giới hạn:

+Bảng biến thiên:

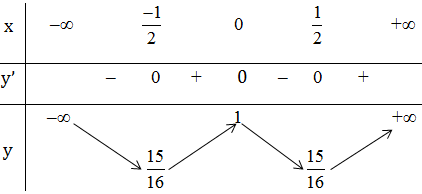
Kết luận: Hàm số đồng biến trên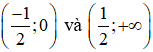

Hàm số nghịch biến trên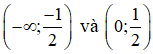

Hàm số đạt cực đại tại x = 0; y_CĐ = 1

Hàm số đạt cực tiểu tại

- Đồ thị:

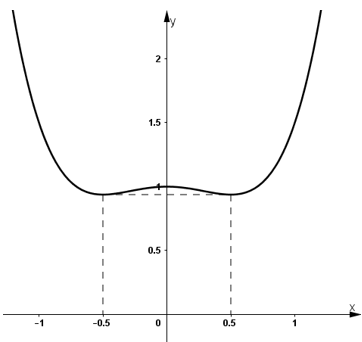
c) Ta có: tung độ y₀ = f(x₀) = 1

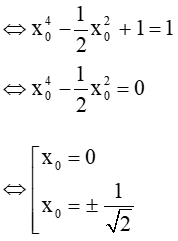
Do đó, có 3 tiếp điểm là (0; 1);

Ta có: y’ = 4x³ – x

Suy ra: y’(0) = 0;

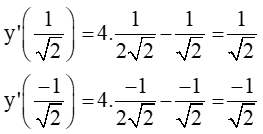
Tại điểm (0; 1) phương trình tiếp tuyến là y = 0(x – 0) + 1 hay y = 1.

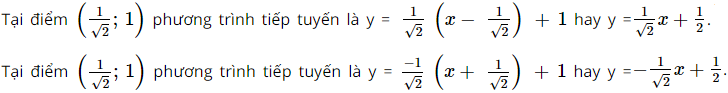
Bài 6 trang 146 SGK

Cho hàm số

a) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số khi m = 2.

b) Viết phương trình tiếp tuyến d của đồ thi (C ) tại điểm M có hoành độ a ≠ -1.

Lời giải:

a) Với m = 2 ta có hàm số

- Tập xác định: D = R\{-1}.

- Sự biến thiên:

⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).

+ Cực trị: hàm số không có cực trị

+ Tiệm cận:

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số

⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.

+ Bảng biến thiên:

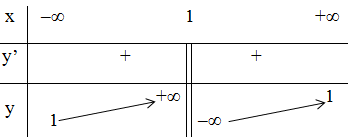
- Đồ thị:

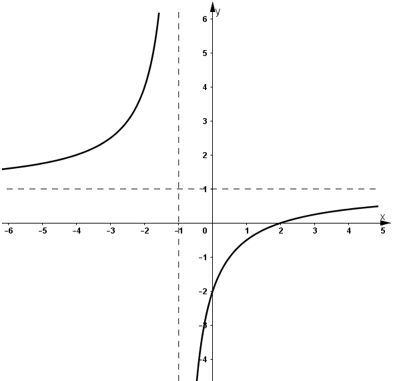
b) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = a là:

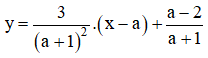
Bài 7 trang 146 SGK

Cho hàm số

 

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Tìm giao điểm của (C) và đồ thị hàm số y = x²+1 . Viết phương trình tiếp tuyến của (C ) tại mỗi giao điểm.

c) Tính thể tích vật tròn xoay thu được khi hình phẳng H giới hạn bởi đồ thị (C) và các đường thẳng y = 0; x = 1 xung quanh trục Ox.

Lời giải:

a) Hàm số

- Tập xác định: D = R\{2}

- Sự biến thiên:

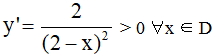
⇒ Hàm số đồng biến trên (-∞; 2) và (2; +∞).

+ Cực trị: Hàm số không có cực trị

+ Tiệm cận: 

⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.

⇒ x = 2 là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

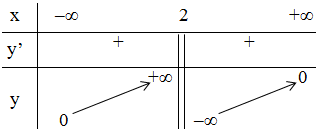
- Đồ thị:

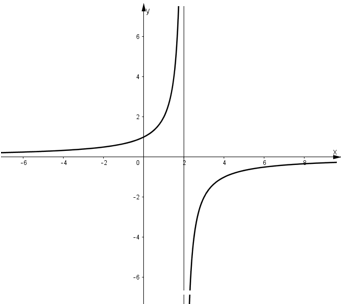
b) Phương trình hoành độ giao điểm của hai đường cong:

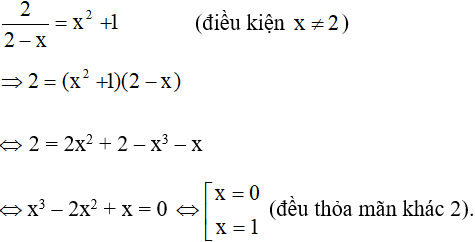
Vậy tọa độ giao điểm của hai đường cong là A(0 ; 1) và B(1 ; 2)

Ta có: y’(0) = ; y’(1) = 2.

+ Phương trình tiếp tuyến tại A là y = (x – 0) + 1 = x + 1

+ Phương trình tiếp tuyến tại điểm B(1 ; 2) là:

y = y’(1).(x – 1) + 2 = 2(x – 1) + 2

Hay y = 2x

c) Thể tích vật tròn xoay thu được khi hình phẳng H giới hạn bởi đồ thị (C) và các đường thẳng y = 0, x = 0, x = 1 xung quanh trục Ox.

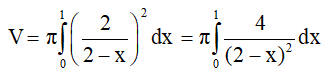
Đặt t = 2 – x. Suy ra: dt = – dx

Đổi cận: với x = 0 thì t = 2;

Với x = 1 thì t = 1.

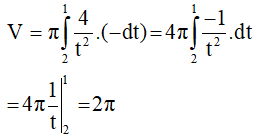
Bài 8 trang 147 SGK

Tìm giá trị lớn nhất và nhỏ nhất của hàm số:

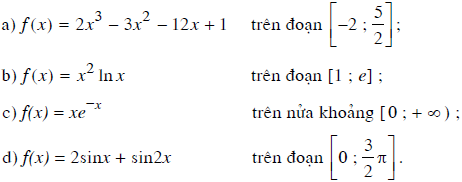
Lời giải:

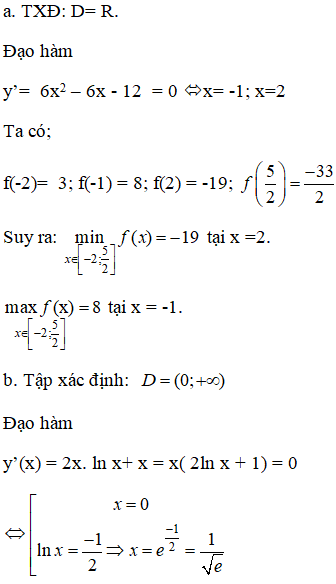
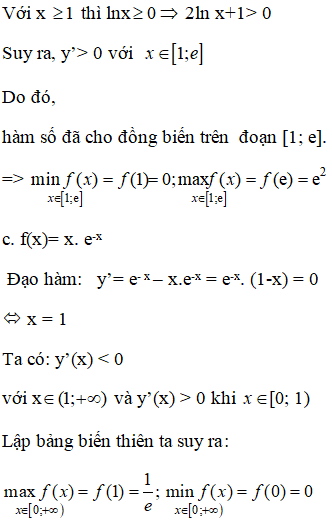
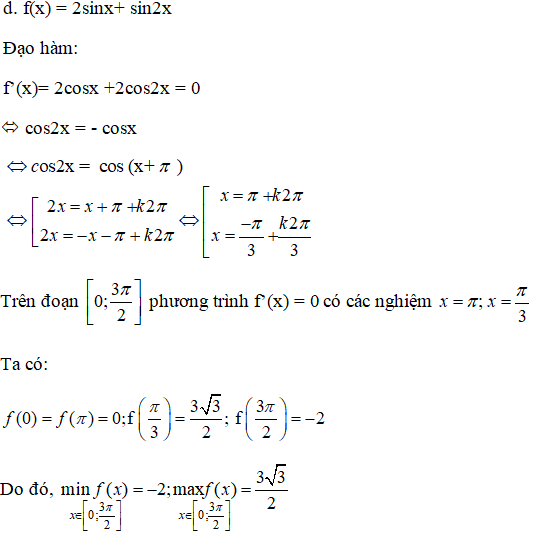
Bài 9 trang 147 SGK

Giải các phương trình sau:

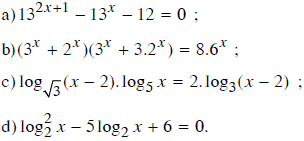
Lời giải:

a. 13^{2x + 1} – 13^x – 12 = 0

⇔ 13.13^2x – 13^x – 12 = 0 (1)

Đặt t = 13^x (t > 0), khi đó (1) trở thành:

13t² – t – 12 = 0 ⇔

Với t = 1 thì 13^x = 1 ⇔ x = 0

Vậy nghiệm của phương trình đã cho là x = 0.

b. (3^x + 2^x).(3^x + 3.2^x) = 8.6^x

⇔ 3^2x + 3.3^x.2^x + 2^x.3^x + 3.2^2x – 8.6^x = 0

⇔ 3^2x + 4.3^x.2^x – 8.2^x.3^x + 3.2^2x = 0

⇔ 3^2x – 4.3^x.2^x + 3.2^2x = 0 (*)

Chia cả hai vế của phương trình trên cho 2^2x ta được:

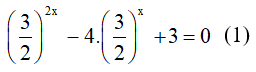
Đặt , khi đó (1) trở thành:

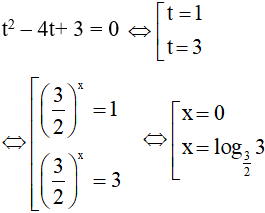
Vậy phương trình có hai nghiệm là x = 0 và x =_^.

c.

Điều kiện:

+ Ta có: 2log₃(x – 2).log₅x – 2.log₃(x – 2) = 0

⇔ 2. log₃(x – 2) (log₅x – 1) = 0

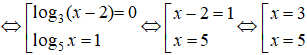
Kết hợp điều kiện, vậy nghiệm phương trình đã cho là x = 3; x = 5.

d.

Điều kiện: x > 0

Đặt t = log₂x, khi đó phương trình đã cho trở thành:

t² – 5t + 6 = 0

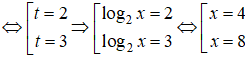
Kết hợp với điều kiện, nghiệm phương trình đã cho là x = 4; x = 8.

Bài 10 trang 147 SGK

Giải các bất phương trình sau:

Lời giải:

a) Điều kiện: 3x ≠ 2x ⇔ x ≠ 0

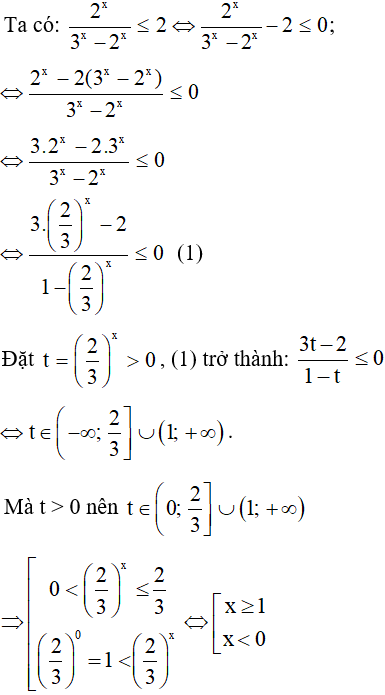
Vậy tập nghiệm của bất phương trình là S = (-∞; 0) ∪ [1; +∞).

c) log²x + 3logx ≥ 4;

Đặt t = logx, bất phương trình trên trở thành:

t² + 3t ≥ 4 ⇔ t² + 3t – 4 ≥ 0

⇔ t ≤ -4 hoặc t ≥ 1

+ Với t ≤ -4 => logx ≤ -4 ⇔ 0 ≤ x ≤ 10^-4

+ Với t ≥ 1 => logx ≥ 1 ⇔ x ≥ 10

Vậy tập nghiệm của bất phương trình là S = (0; 10^-4] ∪ [10; +∞).

d) Điều kiện: x > 0; x ≠

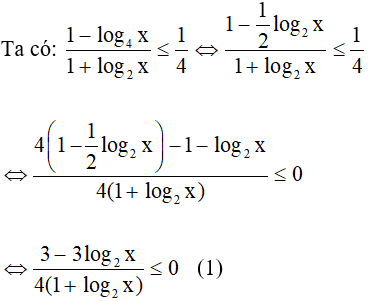
Đặt t = log₂x, (1) trở thành:

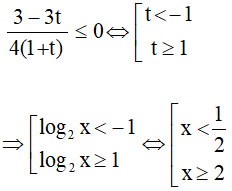
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là S = (0; ) ∪ [2; +∞).

Bài 11 trang 147 SGK

Tính các tích phân sau bằng phương pháp tích phân từng phần:

Lời giải:

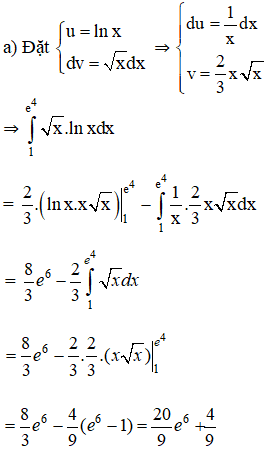
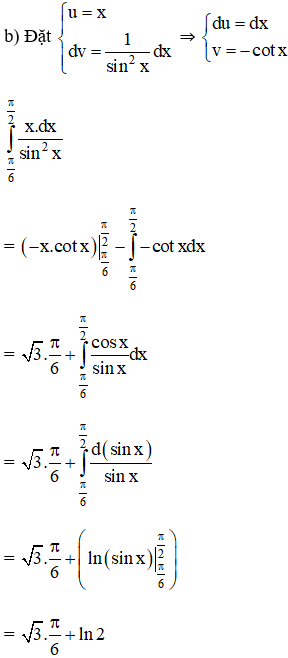
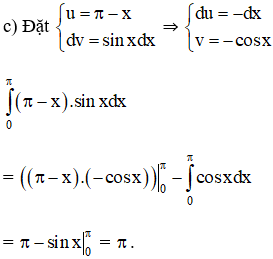
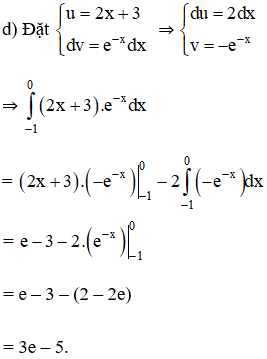
Bài 12 trang 147 SGK

Tính các tích phân sau bằng phương pháp đổi biến số:

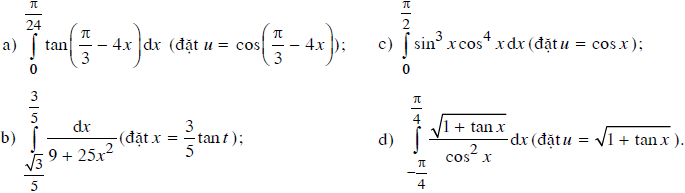
Lời giải:

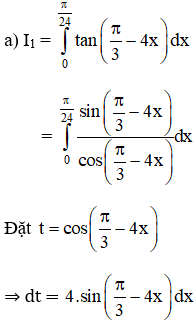
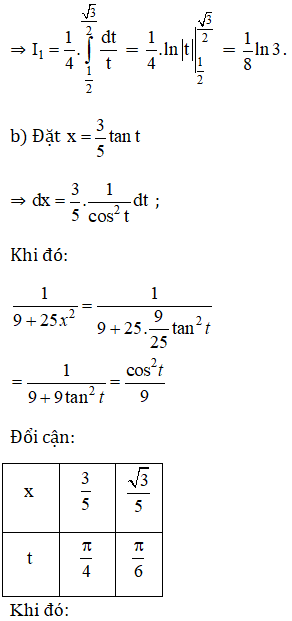
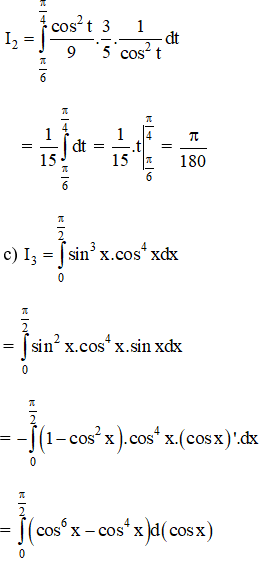
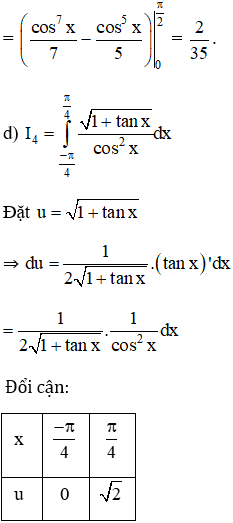
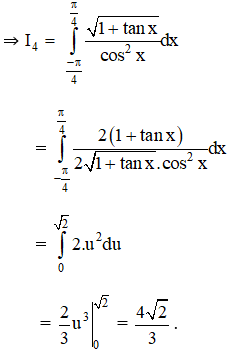
Bài 13 trang 148 SGK

Tính diện tích hình phẳng giới hạn bởi các đường:

a) y = x² + 1; x = -1; x = 2 và các trục hoành.

b) y = ln x; x = ; x = e và trục hoành.

Lời giải:

a) Diện tích cần tính là:

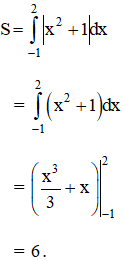
b) Diện tích cần tính là:

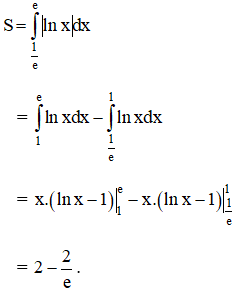
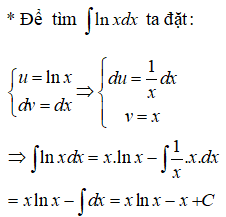
Bài 14 trang 148 SGK

Tìm thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 2x² và y = x³ xung quanh trục Ox.

Lời giải:

Hoành độ giao điểm hai đường cong là nghiệm của phương trình:

2x² = x³ ⇔ x²(2 – x) = 0 ⇔ x = 0 hoặc x = 2.

Vậy thể tích cần tính là:

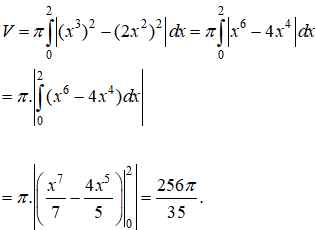
Bài 15 trang 148 SGK

Giải các phương trình sau trên tập số phức:

a) (3 + 2i)z – (4 + 7i) = 2 – 5i

b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z

c) z² – 2z + 13 = 0

d) z⁴ – z² – 6 = 0

Lời giải:

a) (3 + 2i).z – (4 + 7i) = 2 – 5i

⇔ (3 + 2i).z = (2 – 5i) + (4 + 7i)

⇔ (3 + 2i).z = 6 + 2i

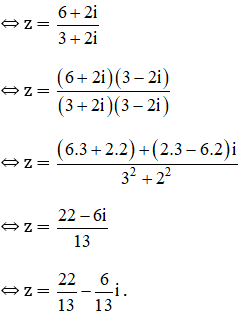
b) (7 – 3i)z + (2 + 3i) = (5 – 4i).z

⇔ [(7 – 3i) – (5 – 4i)].z = –(2 + 3i)

⇔ (2 + i).z = –(2 + 3i)

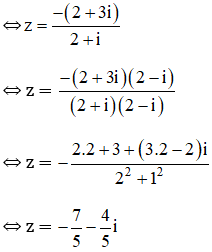
c) z² – 2z + 13 = 0

có Δ' = 1 – 13 = 12 < 0

⇒ Phương trình có hai nghiệm phân biệt:

d) z⁴ – z² – 6 = 0

⇔ (z² + 2)(z² – 3) = 0

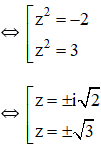
Bài 16 trang 148 SGK

Trên mặt phẳng tọa độ, hãy tìm tập hợp các điểm biểu diễn số phức z thỏa mãn từng bất đẳng thức:

a) |z| < 2;

b) |z – i| ≤ 1;

c) |z – 1 – i| < 1.

Lời giải:

Tập hợp các điểm M(x; y) của mặt phẳng tọa độ biểu diễn số phức z = x + yi thỏa mãn điều kiện:

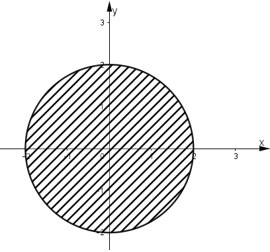
a) |z| < 2

⇔

⇔ x² + y² < 4.

Suy ra, điểm M(x ; y) thuộc hình tròn có tâm O(0 ; 0); bán kính bằng 2 không kể các điểm trên đường tròn.

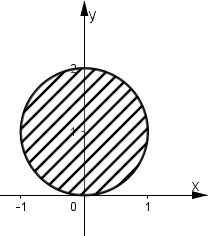
b) Vì z = x + yi nên z – i = x + (y – 1).i

Ta có: |z – i| ≤ 1

⇔

⇔ x² + (y – 1)² ≤ 1.

Tập hợp tất cả các điểm M biểu diễn các số phức z thỏa mãn |z – 1| ≤ 1 là các điểm thuộc hình tròn tâm I(0 ; 1) bán kính bằng 1 kể cả các điểm nằm trên đường tròn.

c) Ta có: z – 1 – i = (x – 1) + (y – 1)i

Để |z – 1 – i| < 1

⇔

⇔ (x – 1)² + (y – 1)² < 1.

Vậy tập hợp các điểm cần tìm là hình tròn (không kể biên) tâm I(1 ; 1), bán kính bằng 1.

 

Sách giáo khoa liên quan