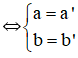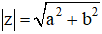Câu hỏi 1 trang 130 SGK
Tìm phần thực và phần ảo của các số phức sau: -3 + 5i, 4 – i√2, 0 + πi, 1 + 0i.
Lời giải:
Số phức -3 + 5i có phần thực là -3; phần ảo là 5;
Số phức 4 – i√2 có phần thực là 4; phần ảo là -√2;
Số phức 0 + πi có phần thực là 0; phần ảo là π;
Số phức 1 + 0i có phần thực là 1; phần ảo là 0.
Câu hỏi 2 trang 131 SGK
Viết số phức z có phần thực bằng ![]() , phần ảo bằng
, phần ảo bằng ![]() .
.
Lời giải:
Số phức đó là z = ![]()
Câu hỏi 3 trang 132 SGK
a) Biểu diễn trên mặt phẳng tọa độ các số phức sau: 3 – 2i, -4i, 3.
b) Các điểm biểu diễn số thực, số thuần ảo nằm ở đâu trên mặt phẳng tọa độ?
Lời giải:
a)
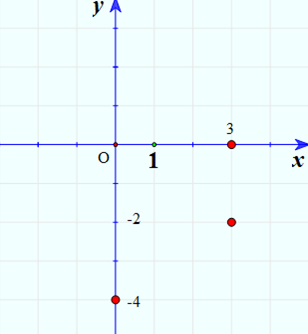
b) Các điểm biểu diễn số thực nằm trên Ox, các điểm biểu diễn số ảo nằm trên Oy.
Câu hỏi 4 trang 132 SGK
Số phức nào có môđun bằng 0?
Lời giải:
Số phức là môđun bằng 0 là z = 0 + 0i.
Câu hỏi 5 trang 132 SGK
Biểu diễn các cặp số phức sau trên mặt phẳng tọa độ và nêu nhận xét:
a) 2 + 3i và 2 – 3i;
b) -2 + 3i và -2 – 3i.
Lời giải:
a)
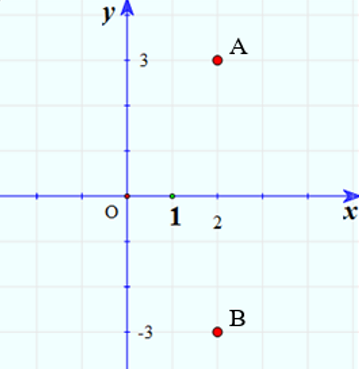
Điểm A(2; 3) biểu diễn số phức 2 + 3i.
Điểm B(2; -3) biểu diễn số phức 2 – 3i.
Nhận xét: Hai điểm biểu diễn hai số phức trên đối xứng nhau qua trục Ox.
b)
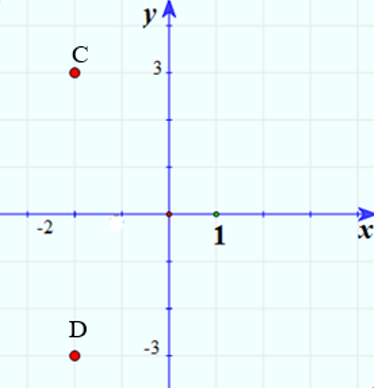
Điểm C(-2; 3) biểu diễn số phức -2 + 3i.
Điểm D(-2; -3) biểu diễn số phức -2 – 3i.
Nhận xét: Hai điểm biểu diễn hai số phức đã cho đối xứng nhau qua trục Ox.
Câu hỏi 6 trang 133 SGK
Cho z = 3 – 2i.
a) Hãy tính . Nêu nhận xét.
b) Tính . Nêu nhận xét.
Lời giải:
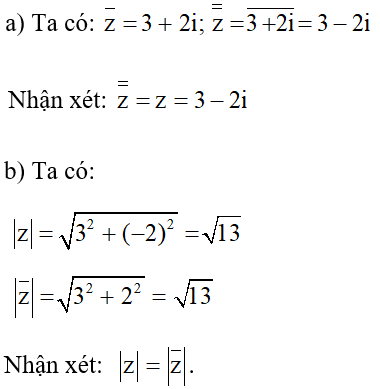
Bài 1 trang 133 SGK
Tìm phần thực và phần ảo của số phức z, biết:
a) z = 1 – πi;
b) z = √2 – i;
c) z = 2√2;
d) z = -7i.
Lời giải:
a) Số phức z = 1 – πi có phần thực: 1, phần ảo: -π
b) Số phức z = √2 – i có phần thực: √2, phần ảo: -1
c) Ta có: z = 2√2 = 2√2 + 0.i
Suy ra, phần thực của số phức là 2√2, phần ảo: 0
d) Ta có: z = -7i = 0 – 7i
Suy ra, phần thực là 0, phần ảo là -7.
Kiến thức áp dụng
| + Mỗi biểu thức có dạng z = a + bi được gọi là một số phức, trong đó: a là phần thực b là phần ảo. + Nếu b = 0 thì z là số thực. Nếu a = 0 thì z được gọi là số ảo. |
Bài 2 trang 133 SGK
Tìm các số thực x và y, biết:
a) (3x – 2) + (2y + 1)i = (x + 1) – (y – 5)i;
b) (1 – 2x) – i√3 = √5 + (1 – 3y)i;
c) (2x + y) + (2y – x)i = (x – 2y + 3) + (y + 2x + 1)i;
Lời giải:
a) (3x – 2) + (2y + 1).i = (x + 1) – (y – 5).i
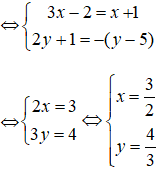
Vậy x = ![]() ; y =
; y = ![]() .
.
b) (1 – 2x) – i√3 = √5 + (1 – 3y)i
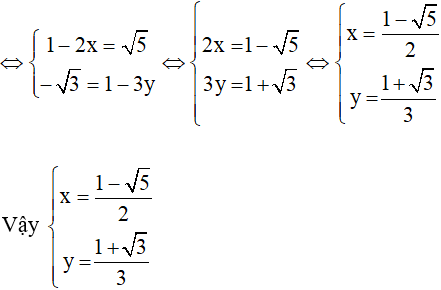
c) (2x + y) + (2y – x)i = (x – 2y + 3) + (y + 2x + 1)i
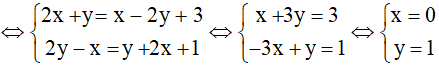
Vậy x = 0; y = 1.
Kiến thức áp dụng
| Hai số phức z = a + bi và z’ = a’ + b’i bằng nhau:
|
Bài 3 trang 134 SGK
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:
a) Phần thực của z bằng -2;
b) Phần ảo của z bằng 3;
c) Phần thực của z thuộc khoảng (-1; 2).
d) Phần ảo của z thuộc đoạn [1; 3];
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2].
Lời giải:
a) Tập hợp các điểm biểu diễn số phức z có phần thực bằng -2 thuộc đường thẳng x = -2.
b) Tập hợp các điểm biểu diễn số phức z có phần ảo bằng 3 thuộc đường thẳng y = 3.
c) Tập hợp các điểm biểu diễn số phức z có phần thực thuộc khoảng (-1; 2) là thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x = 2.
d) Tập hợp các điểm biểu diễn số phức z có phần ảo thuộc đoạn [1; 3] là phần mặt phẳng giới hạn bởi các đường thẳng song song y = 1 và y = 3 (kể cả các điểm thuộc hai đường thẳng đó).
e) Tập hợp các điểm biểu diễn số phức z có phần thực và phần ảo đều thuộc đoạn [-2; 2] là các điểm thuộc (nằm trên và nằm trong hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y = -2, y = 2.
Bài 4 trang 134 SGK
Tính |z|, với:
a) z = -2 + i√3;
b) z = √2 – 3i;
c) z = -5;
d) z = i√3.
Lời giải:
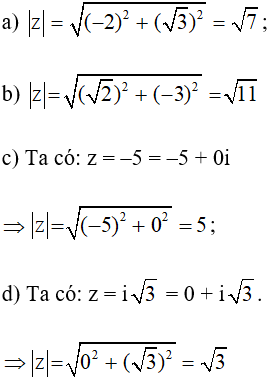
Kiến thức áp dụng
| Môđun của số phức z = a + bi là:
|
Bài 5 trang 134 SGK
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:
a) |z| = 1;
b) |z| ≤ 1;
c) 1< |z| ≤ 2;
d) |z| = 1 và phần ảo của z = 1.
Lời giải:
Gọi số phức z = x + y.i (x; y ∈ ℝ) có điểm biểu diễn là M(x; y).
a) |z| = 1 ⇔ ![]() = 1 ⇔ x2 + y2 = 1
= 1 ⇔ x2 + y2 = 1
Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.
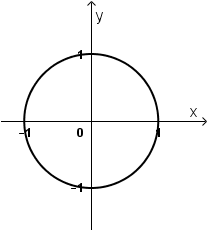
b) |z| ≤ 1 ⇔ ![]() ≤ 1 ⇔ x2 + y2 ≤ 1
≤ 1 ⇔ x2 + y2 ≤ 1
Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1 (kể cả các điểm nằm trên đường tròn).
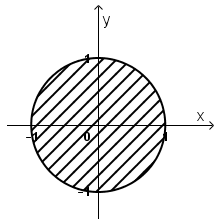
c) Ta có: 1 < |z| ≤ 2
⇔ 1 < ![]() ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1, bán kính đường tròn lớn bằng 2, không tính các điểm thuộc đường tròn nhỏ nhưng có tính các điểm thuộc đường tròn lớn.
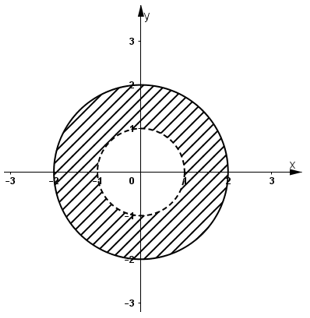
d) Phần ảo của z bằng 1 ⇔ y = 1
Lại có: |z| = 1 ⇔ ![]() = 1
= 1
Mà y = 1 nên x = 0.
Vậy có duy nhất 1 điểm thỏa mãn là M(0; 1).
Kiến thức áp dụng
| Số phức z = x + yi được biểu diễn bởi điểm M(x; y) trên mặt phẳng tọa độ Oxy. |
Bài 6 trang 134 SGK
Tìm ![]() , biết:
, biết:
a) z = 1 – i√2;
b) z = -√2 + i√3;
c) z = 5;
d) z = 7i.
Lời giải:
a) ![]() = 1 + i√2
= 1 + i√2
b) ![]() = -√2 – i√3
= -√2 – i√3
c) Ta có: z = 5 = 5 + 0i
Suy ra: ![]() = 5 – 0i = 5
= 5 – 0i = 5
d) Ta có: z = 7i = 0 + 7i
Suy ra: ![]() = 0 – 7i = -7i
= 0 – 7i = -7i
Kiến thức áp dụng
| Số phức liên hợp của số phức z = a + bi là:
|