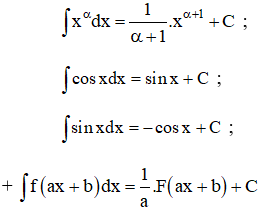Câu hỏi 1 trang 93 SGK
Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:
a) f(x) = 3x2 với x ∈ (-∞; +∞);
b) f(x) = ![]() với x ∈
với x ∈ ![]() .
.
Lời giải:
a) F(x) = x3 vì (x3)' = 3x2
b) F(x) = tanx vì (tanx)' = ![]() .
.
Câu hỏi 2 trang 93 SGK
Hãy tìm thêm những nguyên hàm khác của các hàm số nêu trong Ví dụ 1.
Lời giải:
a) Có thể chọn F(x) = x2 + 8 do (F(x))' = (x2 + 8)’ = 2x + 0 = 2x.
Tổng quát F(x) = x2 + C với C là số thực.
b) Có thể chọn F(x) = lnx + 17, do (F(x))’ = ![]() , x ∈ (0; +∞).
, x ∈ (0; +∞).
Tổng quát F(x) = lnx + C, x ∈ (0;+∞) với C là số thực.
Câu hỏi 3 trang 93 SGK
Hãy chứng minh Định lý 1.
Lời giải:
Vì F(x) là nguyên hàm của f(x) trên K nên (F(x))' = f(x). Vì C là hằng số nên (C)’ = 0.
Ta có:
(G(x))' = (F(x) + C)' = (F(x))' + (C)' = f(x) + 0 = f(x)
Vậy G(x) là một nguyên hàm của f(x).
Câu hỏi 4 trang 95 SGK
Hãy chứng minh Tính chất 3.
Lời giải:
Gọi F(x) là một nguyên hàm của f(x);
G(x) là một nguyên hàm của g(x).
Ta có f(x)=F′(x),g(x)=G′(x).
Suy ra ∫[f(x) ± g(x)]dx = ∫[F′(x) ± G′(x)]dx = ∫[F(x) ± G(x)]′dx = F(x) ± G(x) + C
Lại có ∫f(x)dx ± ∫g(x)dx = ∫F′(x)dx ± ∫G′(x)dx = F(x) ± G(x) + C.
Vậy ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx (đpcm)
Câu hỏi 5 trang 96 SGK
Lập bảng theo mẫu dưới đây rồi dùng bảng đạo hàm trang 77 và trong SGK Đại số và Giải tích 11 để điền vào các hàm số thích hợp vào cột bên phải.
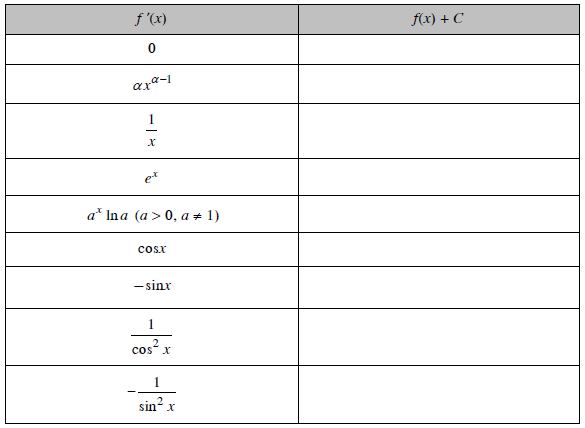
Lời giải:
| f’(x) | f(x) + C |
| 0 | C |
| αxα –1 | xα + C |
| lnx + C nếu x > 0, ln (– x) + C nếu x < 0. | |
| ex | ex + C |
| ax lna (a > 0, a ≠ 1) | ax + C |
| cosx | sin x + C |
| – sinx | cosx + C |
| tanx + C | |
| cotx + C |
Câu hỏi 6 trang 98 SGK
a) Cho ∫(x - 1)10 dx. Đặt u = x – 1, hãy viết (x - 1)10dx theo u và du.
b) Cho ![]() . Đặt x = et, hãy viết
. Đặt x = et, hãy viết ![]() theo t và dt.
theo t và dt.
Lời giải:
a) Ta có du = d(x – 1) = dx.
Suy ra: (x – 1)10dx = u10 du.
b) Ta có dx = d(et) = etdt, do đó ![]() =
= ![]() = tdt.
= tdt.
Câu hỏi 7 trang 99 SGK
Ta có (xcosx)’ = cosx – xsinx
hay - xsinx = (xcosx)’ – cosx.
Hãy tính ∫ (xcosx)’ dx và ∫ cosxdx. Từ đó tính ∫ xsinxdx.
Lời giải:
Ta có ∫ (xcosx)’dx = xcosx + C1 và ∫ cosxdx = sinx + C2.
Từ đó
∫ xsinxdx = - ∫ [(xcosx)’ – cosx]dx = -∫ (xcosx)’dx + ∫ cosxdx = - xcosx – C1 + sinx + C2 = - xcosx + sinx + C.
Kiến thức áp dụng
| Sử dụng công thức ∫f′(x)dx = f(x) + C và các tính chất của nguyên hàm. |
Câu hỏi 8 trang 100 SGK
Cho P(x) là đa thức của x. Từ Ví dụ 9, hãy lập bảng theo mẫu dưới đây rồi điền u và dv thích hợp vào chỗ trống theo phương pháp nguyên phân hàm từng phần.
| ∫ P(x)ex dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | ||
| exdx |
Lời giải:
| ∫ P(x)ex dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | P(x) | P(x)lnx |
| exdx | cosxdx | dx |
Bài 1 trang 100 SGK
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại?
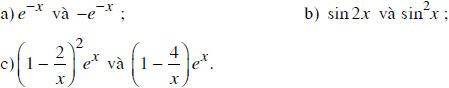
Lời giải:
a) Ta có: (-e-x)' = -e-x.(-x)' = e-x
⇒ -e-x là một nguyên hàm của hàm số e-x
⇒ ∫(e-x)dx = -e-x + C
![]()
Lại có : ( e-x )’ = e-x. (-x)’ = - e-x
Suy ra, e-x là một nguyên hàm của hàm số -e-x
Vậy ∫ -e-xdx = e-x + C
b) (sin2x)' = 2.sinx.(sinx)' = 2.sinx.cosx = sin2x
⇒ sin2x là một nguyên hàm của hàm số.
⇒ ∫sin2xdx = sin2x + C
Kiến thức áp dụng
| + F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu: f’(x) = F(x) + Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì tất cả các hàm số có dạng F(x) + C (C là một hằng số bất kì) đều là nguyên hàm của hàm số f(x). Kí hiệu: ∫f(x)dx = F(x) + C |
Bài 2 trang 100,101 SGK
Tìm nguyên hàm của các hàm số sau?
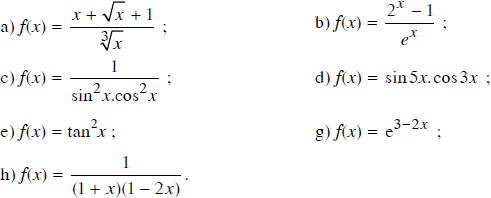
Lời giải:
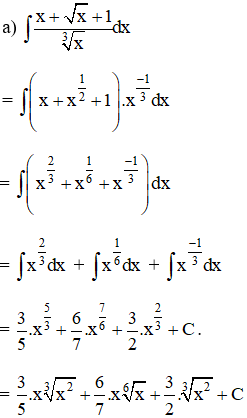
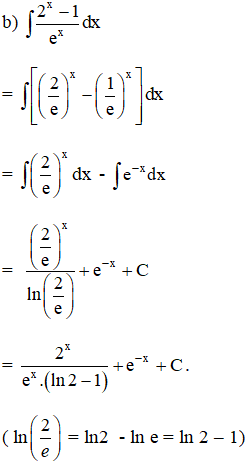
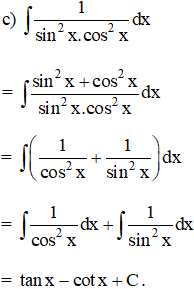
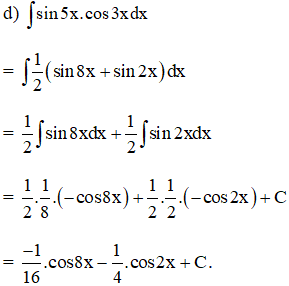
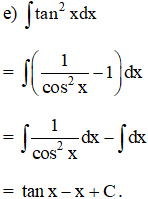
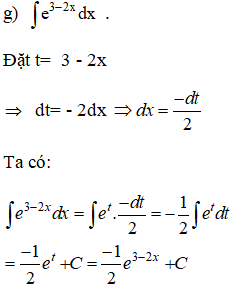
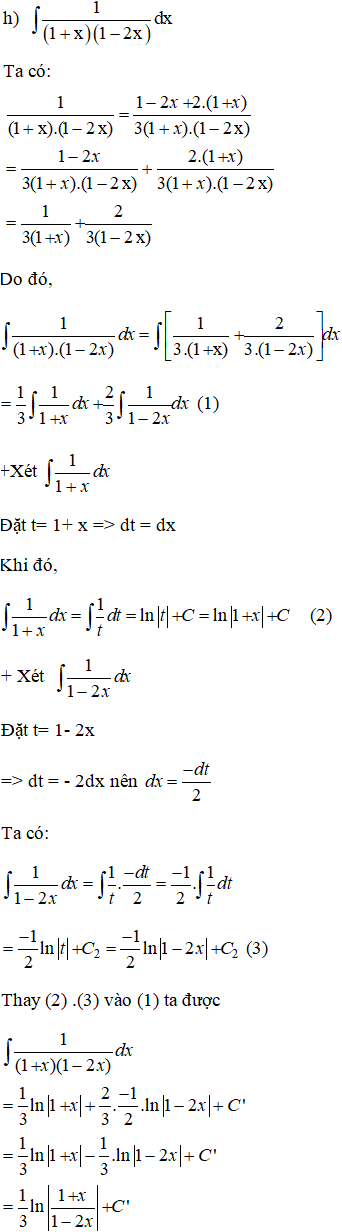
Bài 3 trang 101 SGK
Sử dụng phương pháp biến số, hãy tính:
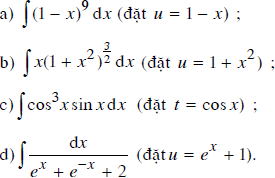
Lời giải:
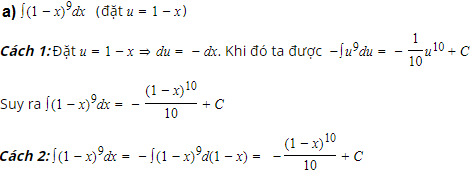
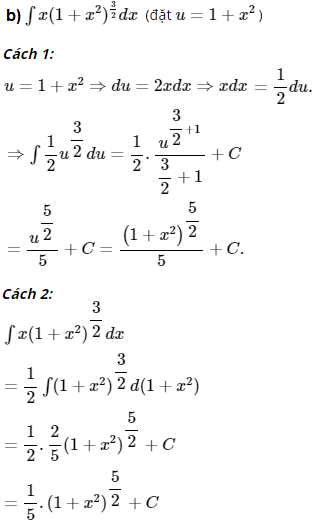
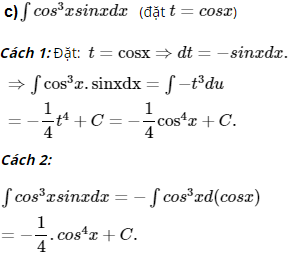
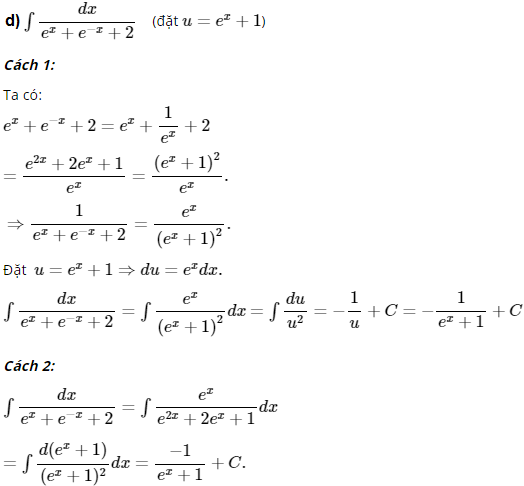
Bài 4 trang 101 SGK
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính:
a) ∫xln(1 + x)dx;
b) ∫(x2 + 2x − 1)exdx;
c) ∫xsin(2x + 1)dx;
d) ∫(1 − x)cosxdx.
Lời giải:
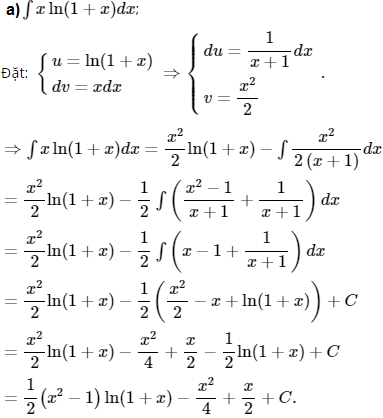
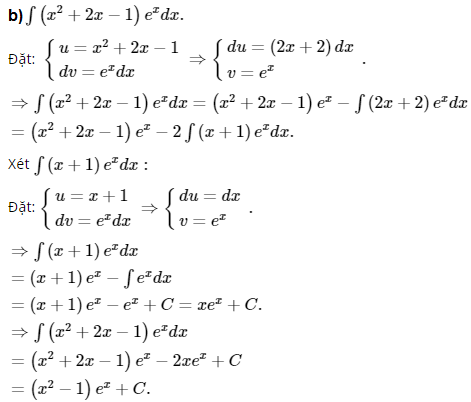
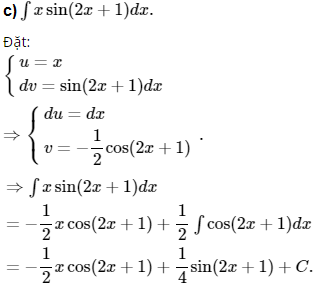
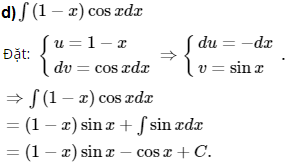
Kiến thức áp dụng
| + Phương pháp nguyên hàm từng phần: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì: ∫u(x).v'(x)dx = u(x).v(x) – ∫u'(x).v(x)dx hay viết ngắn gọn: ∫udv = uv – ∫vdu + Một số công thức nguyên hàm:
|