Câu hỏi 1 trang 13 SGK
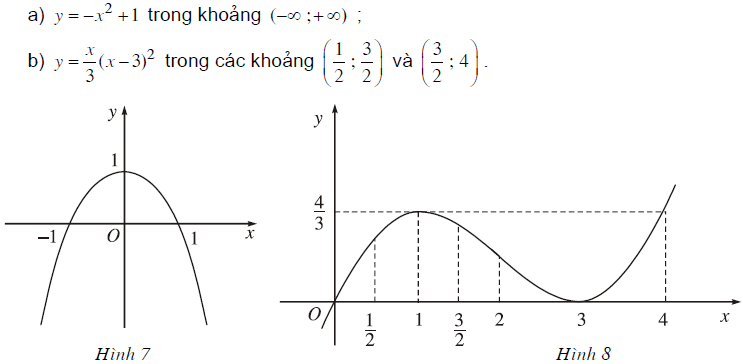
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất)
Xét dấu đạo hàm của các hàm số đã cho và điền vào các bảng dưới đây.
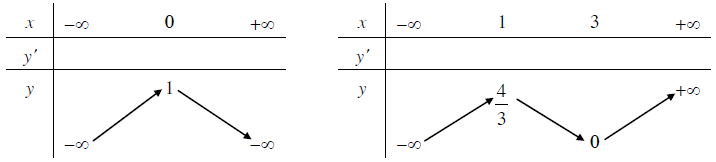
Lời giải:
Quan sát các đồ thị hàm số, ta thấy:
a) Tại x = 0 hàm số có giá trị lớn nhất bằng 1.
Xét dấu đạo hàm:
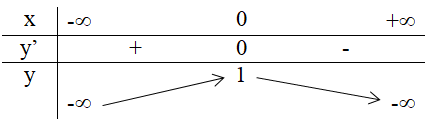
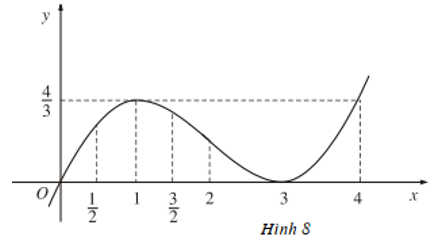
b) Tại x = 1 hàm số có giá trị lớn nhất bằng 4/3.
Tại x = 3 hàm số có giá trị nhỏ nhất bằng 0.
Xét dấu đạo hàm:
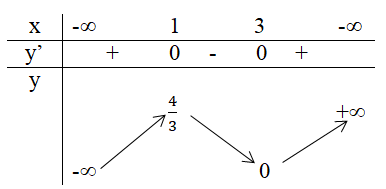
Câu hỏi 2 trang 14 SGK
Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số 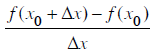 khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
Lời giải:
Với Δx > 0 Ta có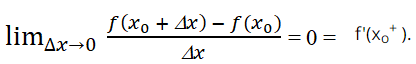
Với Δx < 0 Ta có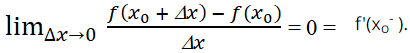
Vậy f’(xo) = 0.
Câu hỏi 3 trang 14 SGK
a) Sử dụng đồ thị, hãy xét xem các hàm số sau đây có cực trị hay không.
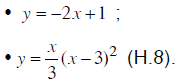
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Lời giải:
a) Hàm số y = – 2x + 1 không có cực trị (vì đồ thị của hàm số là một đường thẳng).
Quan sát Hình 8, ta thấy hàm số y = x/3(x - 3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
b) Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Câu hỏi 4 trang 16 SGK
Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không?
Lời giải:
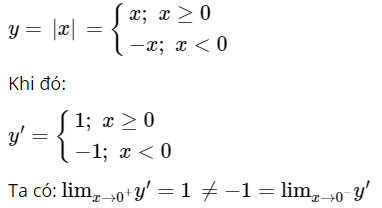
Vậy không tồn tại đạo hàm của hàm số tại x = 0.
Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.
Câu hỏi 5 trang 16 SGK
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số f(x) = x(x2 – 3).
Lời giải:
1. TXĐ: D = ℝ.
Ta có: f(x) = x(x2 – 3) = x3 – 3x
Khi đó: f’(x) = (x3 – 3x)' = 3x2 – 3
2. Cho f’(x) = 0 ⇔ 3x2 – 3 = 0 ⇔ x2 – 1 = 0 ⇔ 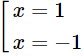
3. Ta có bảng biến thiên:
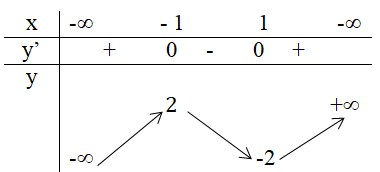
4. Từ bảng biến thiên, ta thấy:
Hàm số đạt cực đại tại x = – 1 và giá trị cực đại là 2.
Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là – 2.
Bài 1 trang 18 SGK
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau:
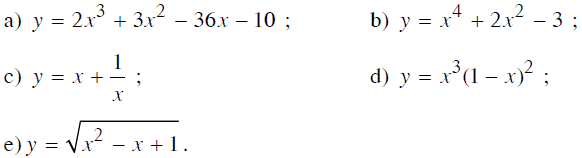
Lời giải:
a) TXĐ: D = ℝ
Ta có: y' = 6x2 + 6x - 36
y' = 0 ⇔ 6x2 + 6x - 36 ⇔
Bảng biến thiên:
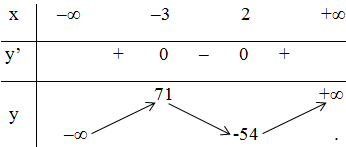
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
b) TXĐ: D = ℝ
Ta có: y'= 4x3 + 4x = 4x(x2 + 1)
y' = 0 ⇔ 4x(x2 + 1) = 0 ⇔ x = 0 (do x2 + 1 > 0 với mọi x)
Bảng biến thiên:
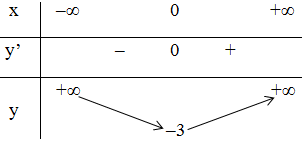
Vậy hàm số đạt cực tiểu tại x = 0; yCT = -3
hàm số không có điểm cực đại.
c) TXĐ: D = ℝ \{0}
Ta có: ![]()
y' = 0 ⇔ 1 - 1/x2 = 0 ⇔ x2 = 1 ⇔ x = ±1
Bảng biến thiên:
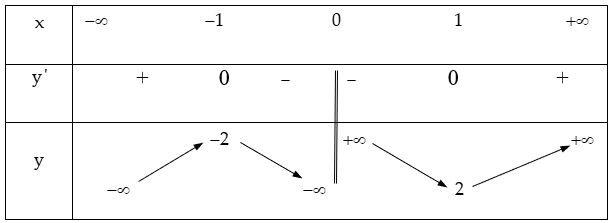
Vậy hàm số đạt cực đại tại x = -1; yCĐ = -2;
hàm số đạt cực tiểu tại x = 1; yCT = 2.
d) TXĐ: D = ℝ
Ta có: y'= (x3)’.(1 – x)2 + x3.[(1 – x)2]’
= 3x2.(1 – x)2 + x3.2(1 – x).(1 – x)’
= 3x2(1 – x)2 - 2x3(1 – x)
= x2.(1 – x)(3 – 5x)
y' = 0 ⇔ x = 0; x = 1 hoặc x = 3/5
Bảng biến thiên:
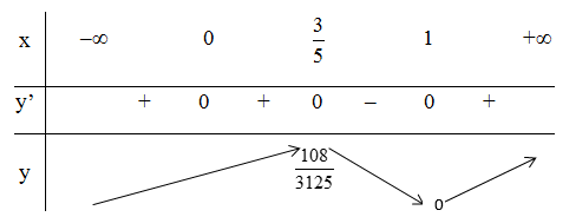
Vậy hàm số đạt cực đại tại x = 3/5, giá trị cực đại là yCĐ = 108/3125.
hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu là yCT = 1.
(Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)
e) Tập xác định: D = ℝ
Ta có:
Có y' = 0 ⇔ 2x - 1 = 0 ⇔ x = 1/2
Bảng biến thiên:
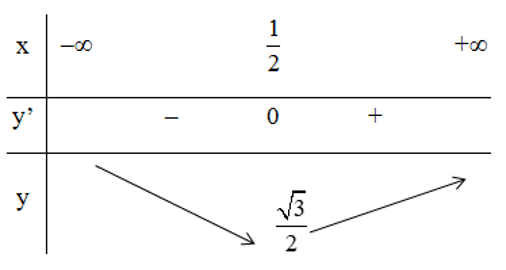
Vậy hàm số đạt cực tiểu tại x = 1/2, giá trị cực tiểu yCT =√3/2.
Bài 2 trang 18 SGK
Áp dụng quy tắc II, hãy tìm các điểm cực trị của hàm số sau:
a) y = x4 - 2x2 + 1;
b) y = sin2x – x;
c) y = sinx + cosx;
d) y = x5 - x3 - 2x + 1.
Lời giải:
a) TXĐ: D = R.
+ y' = 4x3 - 4x
y' = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 hoặc x = ±1.
+ y" = 12x2 - 4
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.
y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.
y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.
b) TXĐ: D = R
+ y' = 2cos 2x – 1;
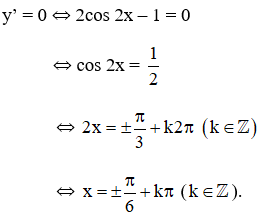
+ y" = -4.sin2x
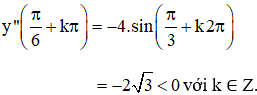
⇒ ![]() (k ∈ Z) là các điểm cực đại của hàm số.
(k ∈ Z) là các điểm cực đại của hàm số.
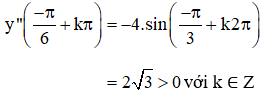
⇒![]() (k ∈ Z) là các điểm cực tiểu của hàm số.
(k ∈ Z) là các điểm cực tiểu của hàm số.
c) TXĐ: D = R
+ y’ = cos x – sin x.
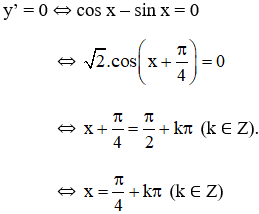
+ y’’ = -sin x – cos x = 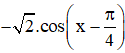
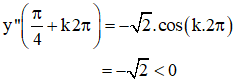
⇒ ![]() là các điểm cực đại của hàm số.
là các điểm cực đại của hàm số.
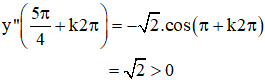
⇒ ![]() là các điểm cực tiểu của hàm số.
là các điểm cực tiểu của hàm số.
d) TXĐ: D = R
+ y'= 5x4 - 3x2 - 2
y' = 0 ⇔ 5x4 – 3x2 – 2 = 0
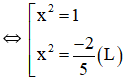
⇔ x = ±1.
+ y" = 20x3 - 6x
y"(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y"(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
Bài 3 trang 18 SGK
Chứng minh rằng hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Lời giải:
Hàm số y =√|x| có tập xác định D = ℝ và liên tục trên ℝ.
+ Chứng minh hàm số ![]() không có đạo hàm tại x = 0.
không có đạo hàm tại x = 0.
Xét giới hạn 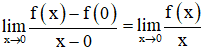 :
:
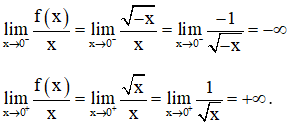
Suy ra không tồn tại giới hạn 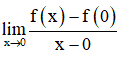
Hay hàm số không có đạo hàm tại x = 0.
+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).
Ta có : f(x) > 0 = f(0) với mọi x thuộc (-1; 1) và x ≠ 0
Do đó hàm số y = f(x) đạt cực tiểu tại x = 0.
Bài 4 trang 18 SGK
Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 - mx2 - 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Lời giải:
TXĐ: D = R
+ y' = 3x2 - 2mx – 2
y’ = 0 ⇔ 3x2 – 2mx – 2 = 0 ⇔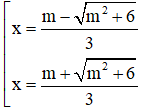
+ y’’ = 6x – 2m.
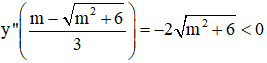
⇒ 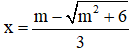 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
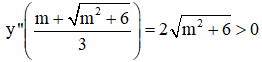
⇒ 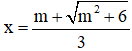 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Bài 5 trang 18 SGK
Tìm a và b để các cực trị của hàm số
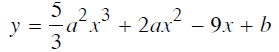 đều là nhưng số dương và
đều là nhưng số dương và 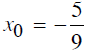 là điểm cực đại.
là điểm cực đại.
Lời giải:
TXĐ: D = ℝ.
Ta có: y’ = 5a2x2 + 4ax – 9.
Suy ra y’’ = 10a2x + 4a
- Nếu a = 0 thì y' = – 9 < 0 với mọi số thực x
Do đó hàm số không có cực trị (loại)
- Nếu a ≠ 0.
y' = 0 ⇔ 5a2x2 + 4ax – 9 = 0
⇔ 5.(ax)2 + 4.ax – 9 = 0
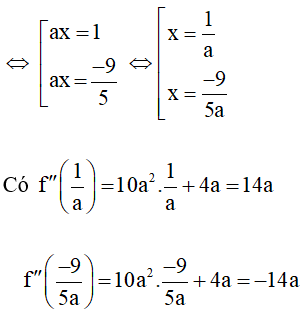
+ TH1: x = 1/a là điểm cực đại
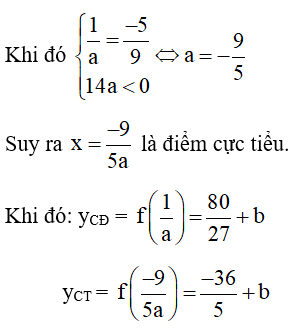
Các cực trị của hàm số đều dương nên
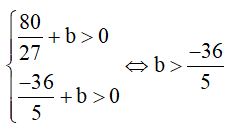
+ TH2: x = −9/5a là điểm cực đại
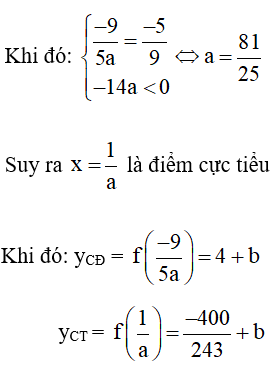
Các cực trị của hàm số đều dương nên

Bài 6 trang 18 SGK
Xác định giá trị của tham số m để hàm số 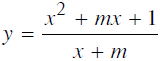 đạt giá trị cực đại tại x = 2.
đạt giá trị cực đại tại x = 2.
Lời giải:
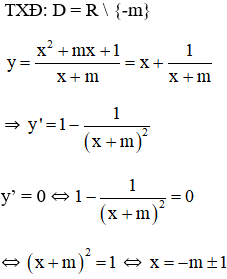
Ta có bảng biến thiên:
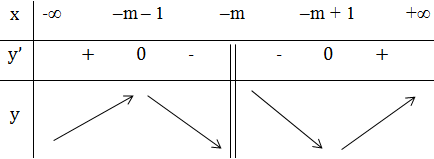
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.


































