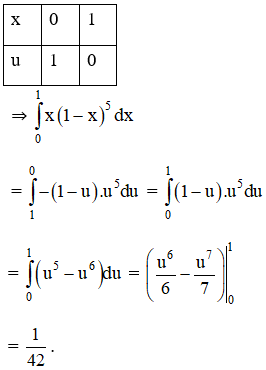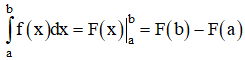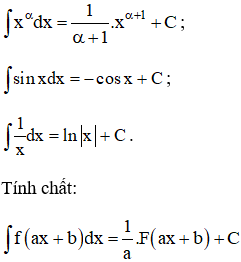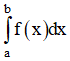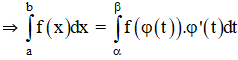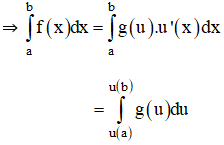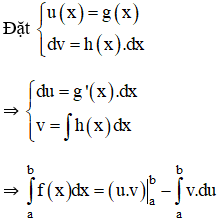Câu hỏi 1 trang 101 SGK
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = 2x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≥ t ≥ 5) (H.45).
1. Tính diện tích S của hình T khi t = 5 (H.46).
2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
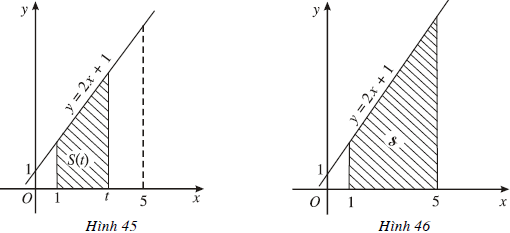
3. Chứng minh rằng S(t) là một nguyên hàm của f(t) = 2t + 1, t ∈ [1; 5] và diện tích S = S(5) – S(1).
Lời giải:
1. Kí hiệu A là điểm có tọa độ (1, 0), D là điểm có tọa độ (5, 0).
Gọi B, C lần lượt là giao điểm của đường thẳng x = 1 và x = 5 với đường thẳng y = 2x + 1.
- Khi đó B và C sẽ có tọa độ lần lượt là (1, 3) và (5, 11).
- Ta có: AB = 3, CD = 11, AD = 4.
Diện tích hình thang ABCD là:
SABCD = ![]() (AB + CD).AD =
(AB + CD).AD = ![]() (3 + 11).4 = 28
(3 + 11).4 = 28
2. Kí hiệu A là điểm có tọa độ (1, 0), D là điểm có tọa độ (5, 0).
Gọi B, C lần lượt là giao điểm của đường thẳng x = 1 và x = 5 với đường thẳng y = 2x + 1.
- Khi đó ta có B (1, 3) và C(t, 2t + 1).
- Ta có AB = 3, AD = t – 1, CD = 2t + 1.
- Khi đó diện tích hình thang ABCD là:
SABCD = ![]() (AB + CD).AD =
(AB + CD).AD = ![]() (3 + 2t + 1).(t – 1) = t2 + t – 2
(3 + 2t + 1).(t – 1) = t2 + t – 2
Vậy S(t) = t2 + t – 2.
3. Vì S’(t) = (t2 + t – 2)’ = 2t + 1 nên hàm số S(t) là một nguyên hàm của hàm số f(t) = 2t + 1, t ∈ [1; 5].
Ta có: S(5) = 52 + 5 – 2 = 28; S(1) = 12 + 1 – 2 = 0
Do đó: S(5) – S(1) = 28 – 0 = 28 = S (đã tính ở câu a)
Vậy S = S(5) – S(1).
Câu hỏi 2 trang 104 SGK
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
Lời giải:
- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
Câu hỏi 3 trang 106 SGK
Hãy chứng minh các tính chất 1 và 2.
Lời giải:
+ Tính chất 1:
- Nếu k = 0 thì tính chất đúng.
- Nếu k ≠ 0 thì ta có ∫k.f(x)dx = k.∫f(x)dx = F(x)
⇒ ∫f(x)dx = ![]()
Khi đó
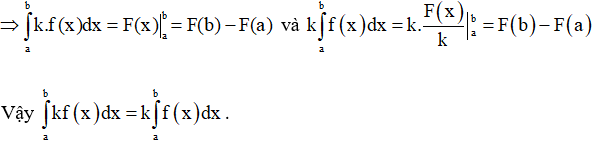
+ Tính chất 2:
Giả sử F(x), G(x) lần lượt là các nguyên hàm của hai hàm số f(x), g(x).
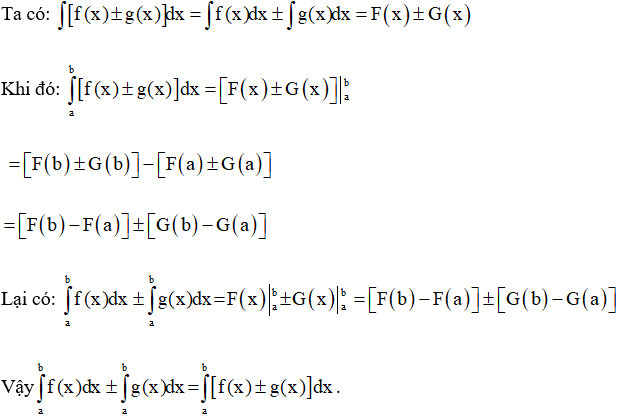
Câu hỏi 4 trang 108 SGK
Cho tích phân 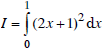 .
.
1. Tính I bằng cách khai triển (2x +1)2.
2. Đặt u = 2x + 1. Biến đổi biểu thức (2x +1)2dx thành g(u)du.
3. Tính 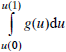 và so sánh kết quả với I trong câu 1.
và so sánh kết quả với I trong câu 1.
Lời giải:
1.
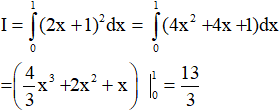
2. Vì u = 2x + 1 nên du = 2dx.
Ta có: (2x +1)2dx = ![]()
3. Ta có: u(1) = 3; u(0) = 1.
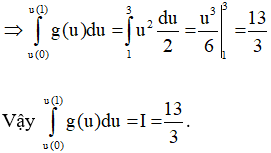
Câu hỏi 5 trang 110 SGK
a) Hãy tính ∫(x+1)exdx bằng phương pháp tính nguyên hàm từng phần.
b) Từ đó tính 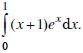
Lời giải:
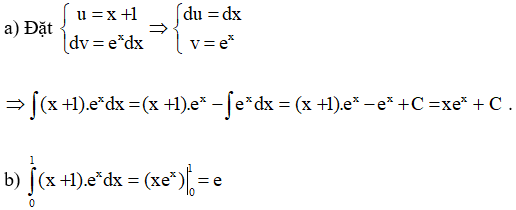
Bài 1 trang 112 SGK
Tính các tích phân sau:
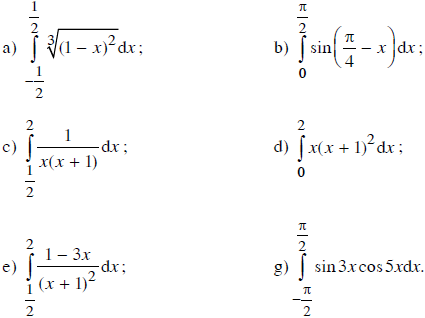
Lời giải:
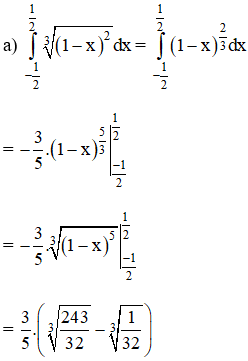
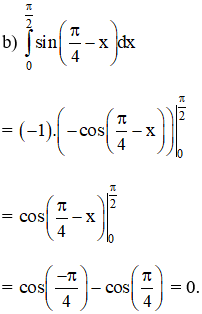
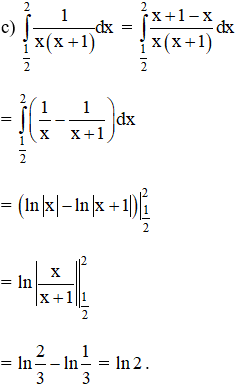
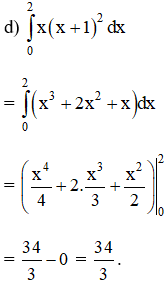
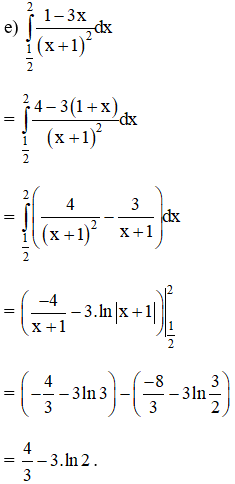
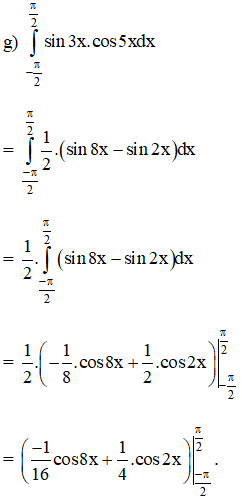
Kiến thức áp dụng
| + Tích phân từ a đến b của hàm số f(x) có nguyên hàm là F(x) là:
+ Một số nguyên hàm sử dụng:
|
Bài 2 trang 112 SGK
Tính các tích phân.

Lời giải:
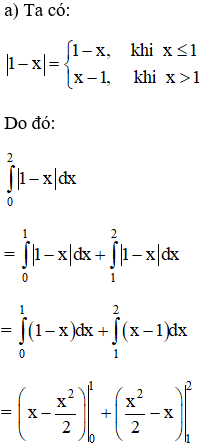
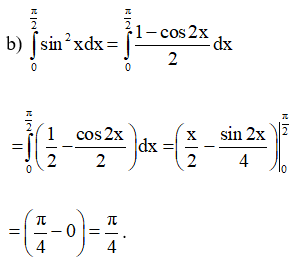
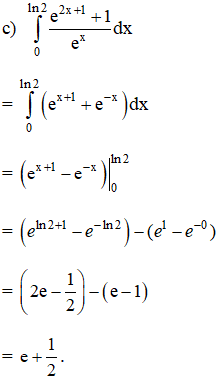
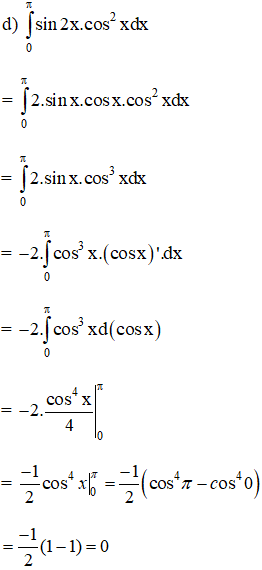
Bài 3 trang 113 SGK
Sử dụng phương pháp biến đổi số, tính tích phân
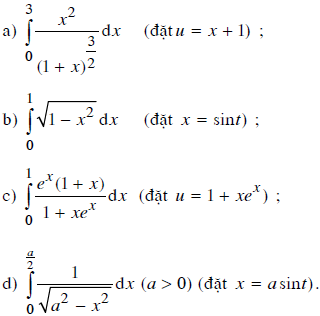
Lời giải:
a) Đặt u = 1 + x. Suy ra: du = dx và x = u – 1 nên x2 = (u – 1)2
Đổi cận:
| x | 0 | 3 |
| u | 1 | 4 |
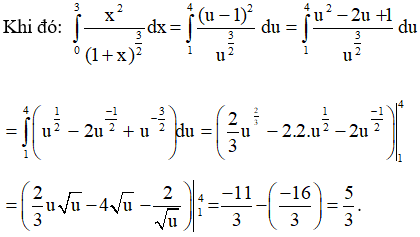
b) Đặt x = sin t (0 < t < ![]() )
)
Suy ra: dx = cost.dt
![]()
Đổi cận:
| x | 0 | 1 |
| t | 0 |
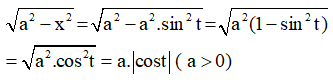
c) Đặt u = 1 + x.ex
Suy ra: du = (ex + xex) dx = ex(1 + x) dx
Đổi cận:
| x | 0 | 1 |
| t | 1 | 1 + e |
Khi đó, ta có:
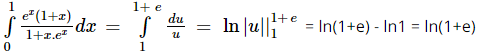
d) Đặt x = a.sint (0 ≤ t < 2π)
Suy ra: dx = a. cost dt.
Ta có:
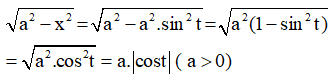
Đổi cận:
| x | 0 | |
| t | 0 |
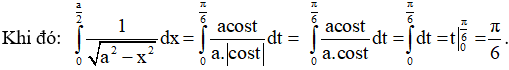
Kiến thức áp dụng
| + Phương pháp đổi biến số tính tích phân Nếu hàm f(x) liên tục trên đoạn [a; b]. Có hai cách đổi biến số: Cách 1: Đặt x = φ(t) ⇒ dx = φ'(t).dt Giả sử φ(α) = a; φ(β) = b.
Cách 2: Đặt u = u(x) ⇒ du = u'(x)dx Giả sử f(x) viết được dưới dạng : f(x) = g(u(x)).u’(x)
|
Bài 4 trang 113 SGK
Sử dụng phương pháp tích phân tưng phần, hãy tính tích phân:
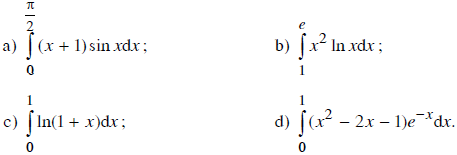
Lời giải:
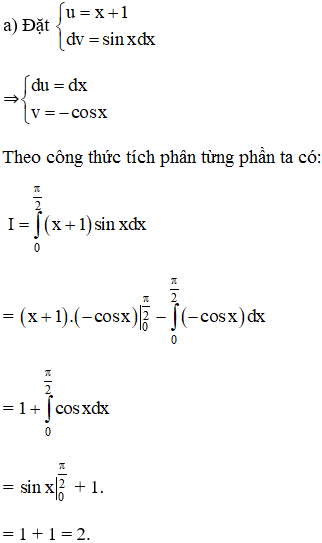
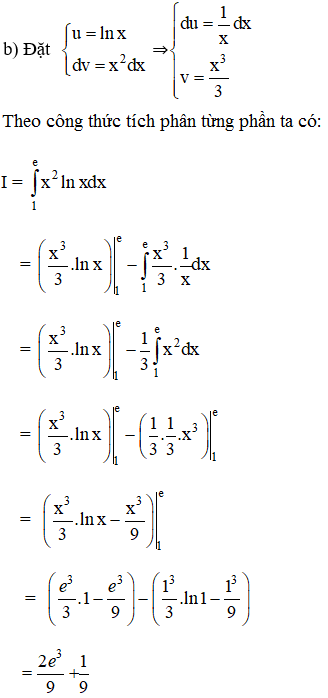


Kiến thức áp dụng
| + Phương pháp tích phân từng phần:
|
Bài 5 trang 113 SGK
Tính các tích phân.
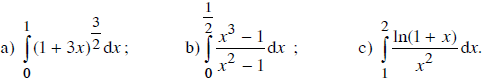
Lời giải:
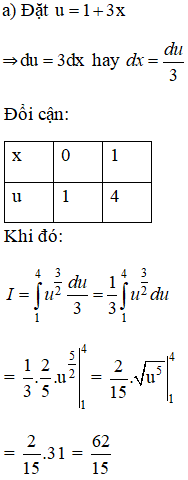
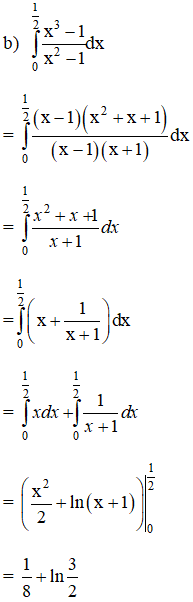

Bài 6 trang 113 SGK
Tính 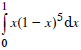 bằng hai phương pháp:
bằng hai phương pháp:
a) Đổi biến số u = 1 – x;
b) Tính tích phân từng phần.
Lời giải:
a) Đặt u = 1 – x;
⇒ du = -dx
Đổi biến: