Câu hỏi 1 trang 20 SGK
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
Lời giải:
a) Ta có: y' = 2x ≤ 0 trên đoạn [-3 ; 0]. Vậy hàm số nghịch biến trên đoạn [-3 ; 0].
Khi đó trên đoạn [-3 ; 0]: hàm số đạt giá trị lớn nhất tại x = -3 và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.
b) Ta có: 
trên đoạn [3 ; 5]. Vậy hàm số nghịch biến trên đoạn [3 ; 5].
Khi đó trên đoạn [3 ; 5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất bằng 3/2.
Câu hỏi 2 trang 21 SGK
Cho hàm số 
có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2 ; 3] và nêu cách tính.
Lời giải:
Giá trị nhỏ nhất của hàm số trên đoạn [-2 ; 3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2 ; 3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.
Câu hỏi 3 trang 23 SGK
Lập bảng biến thiên của hàm số 
Từ đó suy ra giá trị nhỏ nhất của f(x) trên tập xác định.
Lời giải:
1.TXĐ: D = ℝ.
2. 
thì ⇔ x = 0.
3. Bảng biến thiên:
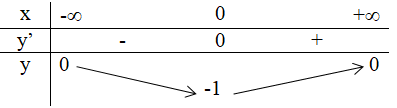
Vậy giá trị nhỏ nhất của hàm số đã cho là – 1 tại x = 0.
Bài 1 trang 23 SGK
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x3 - 3x2 - 9x + 35 trên các đoạn [-4 ; 4] và [0 ; 5];
b) y = x4 - 3x2 + 2 trên các đoạn [0 ; 3] và [2 ; 5];
c) 
trên các đoạn [2 ; 4] và [-3 ; -2];
d) 
trên đoạn [-1 ; 1].
Lời giải:
a) TXĐ: D = R.
y' = 3x2 - 6x - 9;
y' = 0 ⇔ x = –1 hoặc x = 3.
+ Xét hàm số trên đoạn [-4 ; 4] :
y(-4) = -41;
y(-1) = 40;
y(3) = 8
y(4) = 15.
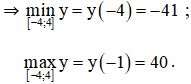
+ Xét hàm số trên [0 ; 5].
y(0) = 35;
y(3) = 8;
y(5) = 40.
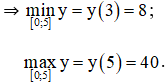
b) TXĐ: D = R
y' = 4x3 - 6x
y’ = 0 ⇔ 2x.(2x2 – 3) = 0 ⇔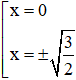 
+ Xét hàm số trên [0 ; 3] :
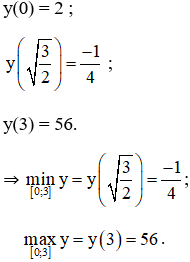
+ Xét hàm số trên [2 ; 5] :
y(2) = 6;
y(5) = 552.
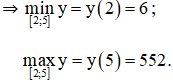
c) TXĐ: D = (-∞; 1) ∪ (1; +∞)
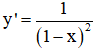> 0 với ∀ x ∈ D.
⇒ hàm số đồng biến trên (-∞ ; 1) và (1 ; +∞).
⇒ Hàm số đồng biến trên [2 ; 4] và [-3 ; -2]
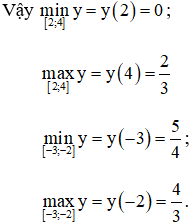
d) TXĐ: D = (-∞ ; 5/4]
Ta có: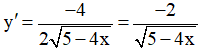 
< 0 với ∀ x ∈ (-∞ ; 5/4)
Suy ra hàm số nghịch biến trên (-∞ ; 5/4)
Do đó hàm số nghịch biến trên [-1 ; 1]
Vậy 
.
Kiến thức áp dụng
| Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên [a; b]. + Tìm các điểm xi trên khoảng (a; b) sao cho tại đó f’(xi) = 0 hoặc không xác định. + Tính f(a); f(xi); f(b). + Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
Nếu hàm số đồng biến trên [a; b] thì
Nếu hàm số nghịch biến trên [a; b] thì
|
Bài 2 trang 24 SGK
Trong số các hình chữ nhật cùng có chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Lời giải:
Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
S = x(8 – x) = 8x – x2 = 16 – (16 – 8x + x2) = 16 – (x – 4)2 ≤ 16.
⇒ Smax = 16
Dấu bằng xảy ra khi (x – 4)2 = 0 ⇔ x = 4.
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16cm2.
Kiến thức áp dụng
| Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x thuộc D và tồn tại xo ∈ D để f(xo) = M. |
Bài 3 trang 24 SGK
Trong tất cả các hình chữ nhật cùng có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Lời giải:
Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
Suy ra độ dài cạnh còn lại là: 
(m)
Do đó chu vi hình chữ nhật:
Xét hàm số 
trên (0 ; +∞)
Ta có: P'(x) = 2 - 96/x2
P'(x) = 0 ⇔ 2 - 96/x2 = 0
⇔ x2 = 48 => x = 4√3
Bảng biến thiên trên (0; +∞):
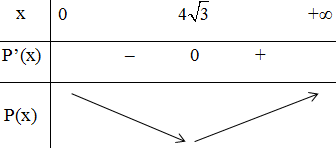
Suy ra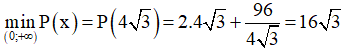 
Suy ra cạnh của hình chữ nhật là x = 4√3 và 48/x = 48/4√3 = 4√3
Vậy trong các hình chữ nhật có cùng diện tích 48 m2 thì hình vuông cạnh 4√3 m có chu vi nhỏ nhất.
Kiến thức áp dụng
| Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x thuộc D và tồn tại xo ∈ D để f(xo) = M. |
Bài 4 trang 24 SGK
Tính giá trị lớn nhất của các hàm số sau:
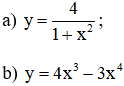
Lời giải:
a) TXĐ: D = R
Ta thấy: 1 + x2 ≥ 1
⇒ 
đạt được khi 1 + x2 = 1 ⇔ x = 0.
b) TXĐ : D = R
⇒ y' = 12x2 - 12x3 = 12x2(1 - x)
y' = 0 ⇔ x = 0 hoặc x = 1
Bảng biến thiên:
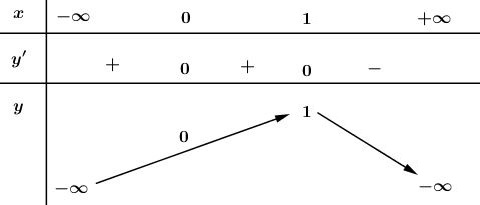
Từ bảng biến thiên suy ra: max y = y(1) = 1.
Kiến thức áp dụng
| Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x thuộc D và tồn tại xo ∈ D để f(xo) = M. |
Bài 5 trang 24 SGK
Tính giá trị nhỏ nhất của các hàm số sau:
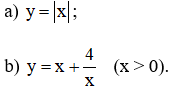
Lời giải:
a)
- Cách 1:
Ta có: y = |x| ≥ 0 ∀ x
⇒ Hàm số có giá trị nhỏ nhất là min y = 0 khi x = 0.
- Cách 2:
Bảng biến thiên:
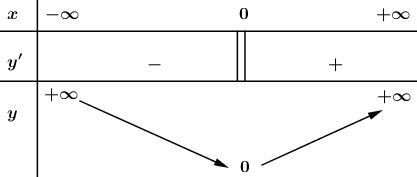
Từ bảng biến thiên suy ra: min y = 0
b) D = (0 ; +∞)
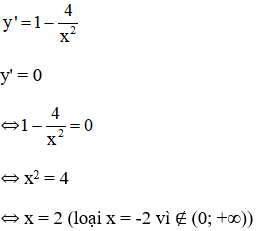
Bảng biến thiên:
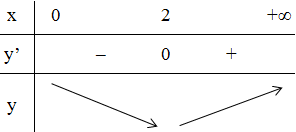
Từ bảng biến thiên suy ra: min y = y(2) = 4
Kiến thức áp dụng
| Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x thuộc D và tồn tại xo ∈ D để f(xo) = M. |
