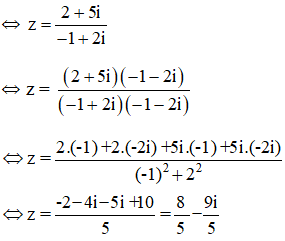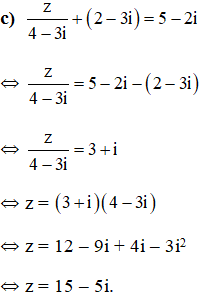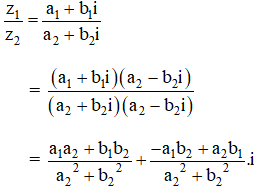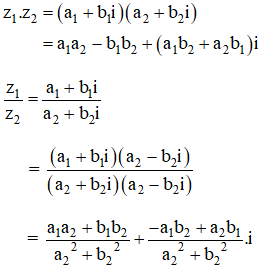Câu hỏi 1 trang 136 SGK
Cho z = 2 + 3i. Hãy tính Hãy tính và
. Nêu nhận xét.
Lời giải:
Nhận xét:
Tổng của hai số phức liên hợp của nhau là một số thực và tổng này bằng hai lần phần thực của số phức đó.
Tích của hai số phức liên hợp của nhau là một số thực và tổng này bằng bình phương môđun của số phức đó.
Câu hỏi 2 trang 138 SGK
Thực hiện các phép chia sau:
![]()
Lời giải:
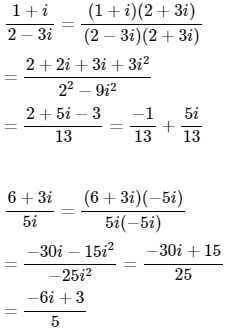
Bài 1 trang 138 SGK
Thực hiện các phép chia sau:
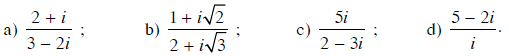
Lời giải:
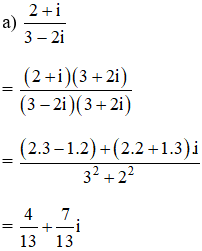
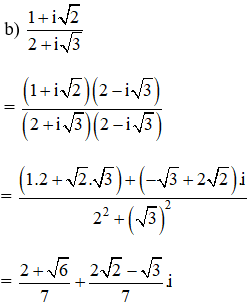
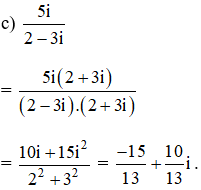
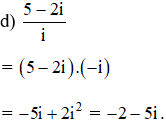
Kiến thức áp dụng
| Chia số phức z1 = a1 + b1i cho z2 = a2 + b2i.
|
Bài 2 trang 138 SGK
Tìm nghịch đảo ![]() của số phức z, biết:
của số phức z, biết:
a) z = 1 + 2i;
b) z = √2 – 3i;
c) z = i;
d) z = 5 + i√3.
Lời giải:
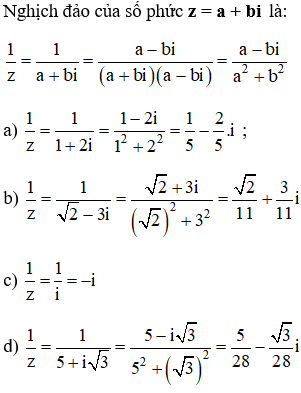
Bài 3 trang 138 SGK
Thực hiện các phép tính sau:
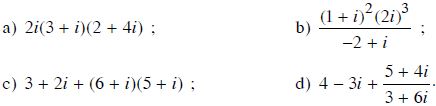
Lời giải:
a) 2i(3 + i)(2 + 4i)
= (6i + 2i2)(2 + 4i)
= (-2 + 6i)(2 + 4i)
= (-2.2 – 6.4) + (6.2 – 2.4).i
= -28 + 4i.
b) Ta có:
(1 + i)2.(2i)3 = (1 + 2i + i2).8i.i2
= (1 + 2i – 1).8i .(-1) = -16i2 = 16.
Do đó:
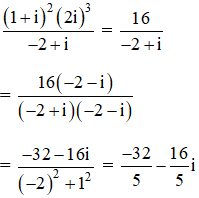
c) 3 + 2i + (6 + i)(5 + i)
= 3 + 2i + (6.5 – 1.1) + (6.1 + 5.1).i
= 3 + 2i + 29 + 11i
= 32 + 13i.
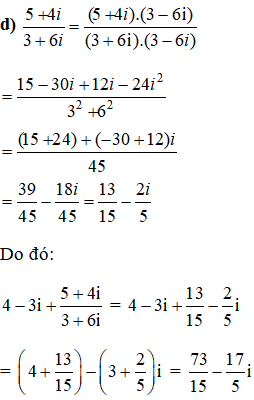
Kiến thức áp dụng
| Chia số phức z1 = a1 + b1i cho z2 = a2 + b2i.
|
Bài 4 trang 138 SGK
Giải các phương trình sau:
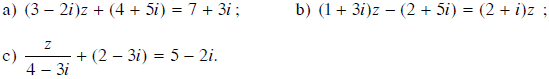
Lời giải:
a) (3 – 2i)z + (4 + 5i) = 7 + 3i
⇔ (3 – 2i).z = (7 + 3i) – (4 + 5i)
⇔ (3 – 2i).z = 3 – 2i
⇔ z = 1.
b) (1 + 3i)z – (2 + 5i) = (2 + i)z
⇔ (1 + 3i).z – (2 + i).z = 2 + 5i
⇔ [(1 + 3i) – (2 + i)].z = 2 + 5i
⇔ (-1 + 2i).z = 2 + 5i