Câu hỏi 1 trang 27 SGK
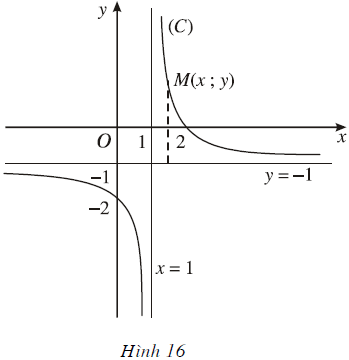
Cho hàm số 
có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞.
Lời giải:
Khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞ dần tiến về 0.
Câu hỏi 2 trang 29 SGK
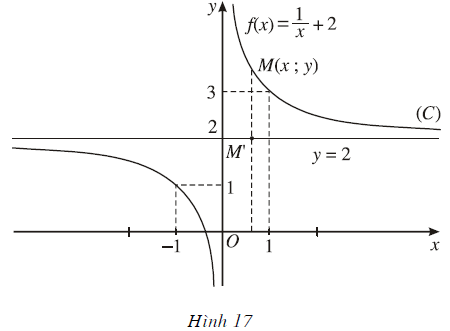
Tính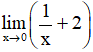 
và nêu nhận xét về khoảng cách MH khi x → 0 (H.17)
Lời giải:
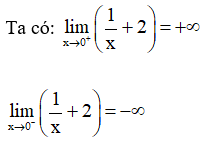
Nhận xét: Khi x dần đến 0 thì độ dài đoạn thẳng MH dần tiến đến 0.
Bài 1 trang 30 SGK
Tìm các tiệm cận của đồ thị hàm số:
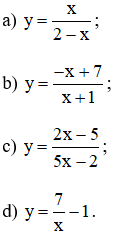
Lời giải:
a) Ta có: 
Suy ra đồ thị hàm số có tiệm cận đứng là x = 2.
Lại có: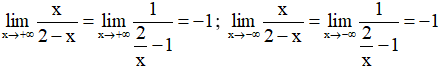 
Suy ra đồ thị hàm số có tiệm cận ngang là y = –1.
b) Ta có: 
Suy ra đồ thị hàm số có tiệm cận đứng là x = –1.
Lại có: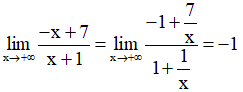 
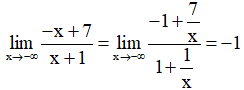
Suy ra đồ thị hàm số có tiệm cận ngang là y = –1.
c) Ta có: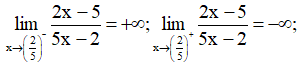 
Suy ra đồ thị hàm số có tiệm cận đứng là x = 2/5.
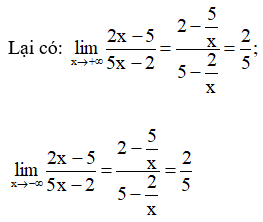
Suy ra đồ thị hàm số có tiệm cận ngang là y = 2/5.
d) Ta có: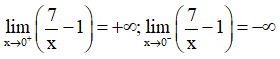 
Suy ra đồ thị hàm số có tiệm cận đứng là x = 0 (trục Oy)
Lại có: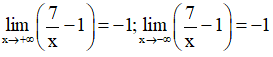 
Suy ra đồ thị hàm số có tiệm cận ngang là y = -1.
Kiến thức áp dụng
| Hàm số y = f(x) xác định trên một khoảng vô hạn. + Nếu có + Nếu có ít nhất 1 trong các điều kiện: * Lưu ý : Có thể có hai hoặc nhiều tiệm cận ngang hoặc tiệm cận đứng. |
hoặc 
thì y = y0 là tiệm cận ngang của đồ thị hàm số.
hoặc 
hoặc 
hoặc 
thì đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số.Bài 2 trang 30 SGK
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:
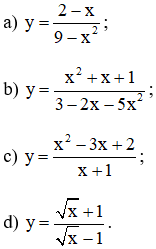
Lời giải:
a) Ta có: 
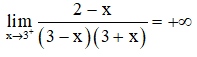
Suy ra x = 3 là tiệm cận đứng của đồ thị hàm số.
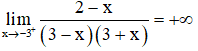
Suy ra x = -3 là một tiệm cận đứng khác của đồ thị hàm số.
Lại có: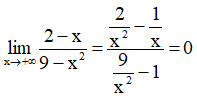 
Suy ra y = 0 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có hai đường tiệm cận đứng là x = -3 và x = 3; đường tiệm cận ngang là y = 0.
b) Ta có: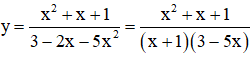 
Do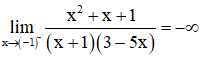 
Suy ra x = -1 là tiệm cận đứng của đồ thị hàm số.
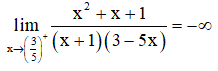
Suy ra 
là tiệm cận đứng của đồ thị hàm số.
Lại có: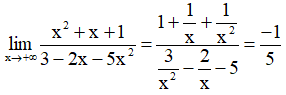 
Suy ra 
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có hai đường tiệm cận đứng là x = -1 ; 
và một tiệm cận ngang là 
.
c) Ta có: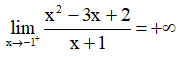 
Suy ra đồ thị có tiệm cận đứng là x = -1.
Lại có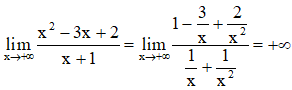 
Suy ra đồ thị không có tiệm cận ngang.
Vậy đồ thị hàm số có một tiệm cận đứng là x = -1.
d) Ta có: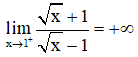 
Suy ra x = 1 là tiệm cận đứng của đồ thị hàm số.
Lại có: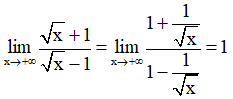 
Suy ra y = 1 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng là x = 1 và một tiệm cận ngang là y = 1.
Kiến thức áp dụng
| Hàm số y = f(x) xác định trên một khoảng vô hạn. + Nếu có + Nếu có ít nhất 1 trong các điều kiện: * Lưu ý : Có thể có hai hoặc nhiều tiệm cận ngang hoặc tiệm cận đứng. |
