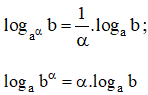Câu hỏi 1 trang 80 SGK
Giải phương trình 62x – 3 = 1 bằng cách đưa về dạng aA(x) = aB(x) và giải phương trình A(x) = B(x).
Lời giải:
Ta có: 62x - 3 = 1 ⇔ 62x - 3 = 60 ⇔ 2x - 3 = 0 ⇔ x = 3/2.
Vậy nghiệm của phương trình là x = 3/2.
Câu hỏi 2 trang 81 SGK
Giải phương trình 
.52x + 5.5x = 250 bằng cách đặt ẩn phụ t = 5x.
Lời giải:
Đặt t = 5x (t > 0), ta có:
. 52x + 5 . 5x = 250
⇔ 
. t2 + 5t = 250
⇔ t2 + 25t - 1250 = 0
⇔ t = 25 hoặc t = – 50 (loại)
Khi đó 5x = 25 ⇔ 5x = 52 ⇔ x = 2.
Vậy nghiệm của phương trình đã cho là x = 2.
Câu hỏi 3 trang 81 SGK
Tính x, biết log3x = 1/4.
Lời giải:
ĐKXĐ: x > 0
Theo định nghĩa logarit ta có:
log3x = 1/4 ⇔ x = 31/4 (t/m)
Vậy x = 31/4.
Câu hỏi 4 trang 82 SGK
Cho phương trình log3x + log9x = 6. Hãy đưa các lôgarit ở vế trái về cùng cơ số.
Lời giải:
Ta có:
log9x = log32x = 1/2 log3x.
Vậy phương trình đã cho tương đương với phương trình:
log3x + 1/2 log3x = 6.
Câu hỏi 5 trang 83 SGK
Giải phương trình (log2x)2 − 3log2x + 2 = 0 bằng cách đặt ẩn phụ t = log2x.
Lời giải:
Đặt t = log2x.
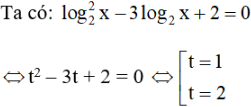
Với t = 1 thì log2x = 1 ⇔ x = 21 = 2
Với t = 2 thì log2x = 2 ⇔ x = 22 = 4
Vậy nghiệm của phương trình là x = 2, x = 4.
Câu hỏi 6 trang 83 SGK
Giải phương trình log1/2x + (log2x)2 = 2.
Lời giải:
ĐKXĐ: x > 0
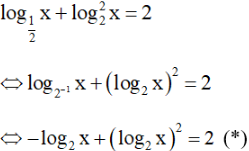
Đặt t = log2x
Khi đó (*) ⇔ -t + t2 = 2 ⇔ t2 − t − 2 = 0 ⇔ t = 2 hoặc t = -1
Với t = 2 thì log2x = 2 ⇔ x = 22 = 4 (t/m)
Với t = -1 thì log2x = -1 ⇔ x = 2-1 = 1/2
Vậy x = 4, x = 1/2 là nghiệm của phương trình đã cho.
Bài 1 trang 84 SGK
Giải các phương trình mũ:
Lời giải:
Bài 2 trang 84 SGK
Giải các phương trình mũ:
a) 32x−1 + 32x = 108;
b) 2x+1 + 2x−1 + 2x = 28;
c) 64x − 8x −56 = 0;
d) 3.4x − 2.6x = 9x.
Lời giải:
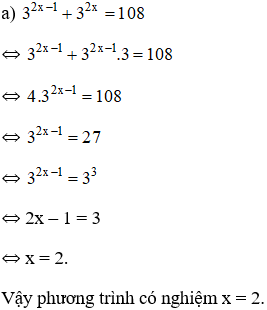
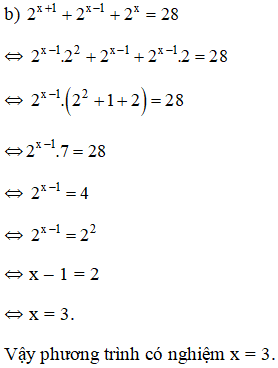
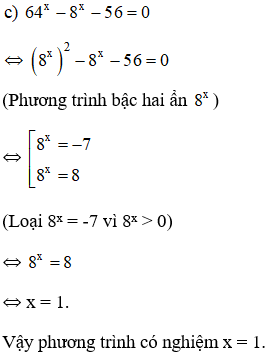
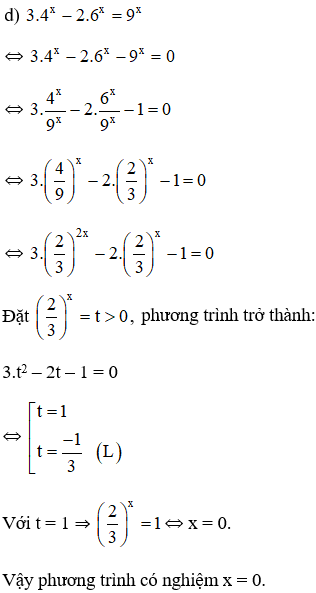
Kiến thức áp dụng
| Một số phương pháp giải phương trình mũ đơn giản: + Đưa về cùng cơ số:
+ Đặt ẩn phụ + Lôgarit hóa |
Bài 3 trang 84 SGK
Giải các phương trình logarit:
a) log3(5x + 3) = log3(7x + 5);
b) log(x − 1) − log(2x − 11) = log2;
c) log2(x − 5) + log2(x + 2) = 3;
d) log(x2 − 6x + 7) = log(x − 3).
Lời giải:
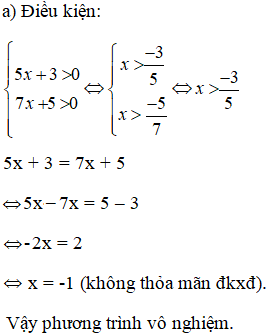
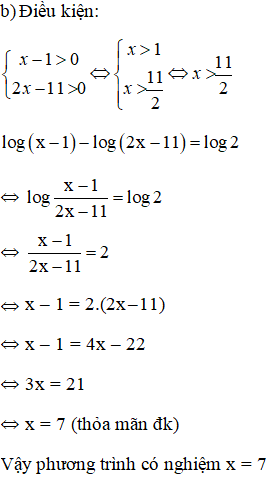
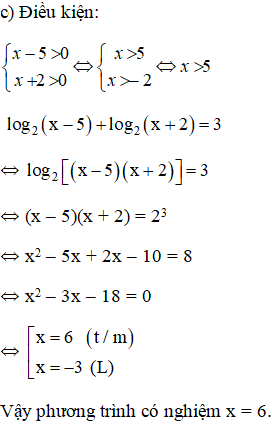
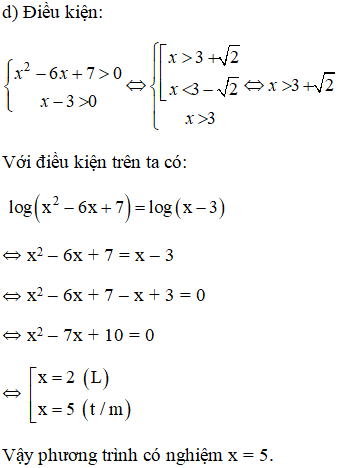
Kiến thức áp dụng
| Một số cách giải phương trình lôgarit đơn giản: + Đưa về cùng cơ số: logaf(x) = logag(x) ⇔ f(x) = g(x) + Đặt ẩn phụ + Mũ hóa: logaf(x) = b ⇔ f(x) = ab |
Bài 4 trang 85 SGK
Giải các phương trình lôgarit:
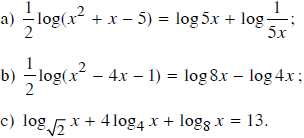
Lời giải:
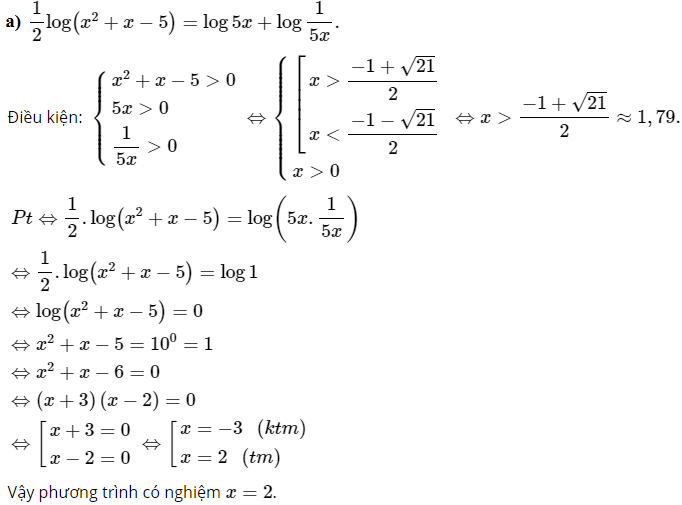
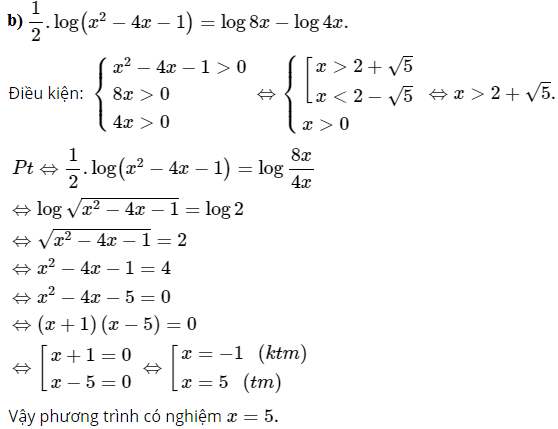
Kiến thức áp dụng
| Một số cách giải phương trình lôgarit đơn giản: + Đưa về cùng cơ số: logaf(x) = logag(x) ⇔ f(x) = g(x) + Đặt ẩn phụ + Mũ hóa: logaf(x) = b ⇔ f(x) = ab - Một số công thức biến đổi lôgarit:
|
