Bài giải GIẢI TÍCH 12 - Ôn tập chương I | Sách Bài Giải

Bài 1 trang 45 SGK

Phát biểu các điều kiện để hàm số đồng biến, nghịch biến. Tìm các khoảng đơn điệu của các hàm số

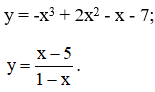
Lời giải:

- Điều kiện đồng biến, nghịch biến của hàm số:

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.

+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.

- Xét hàm số y = -x³ + 2x² – x – 7, ta có:

y' = -3x² + 4x – 1

+ Hàm số đồng biến

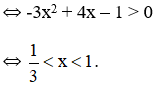
+ Hàm số nghịch biến

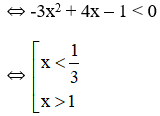
Vậy hàm số đồng biến trên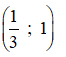

nghịch biến trên các khoảng 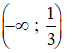và (1 ; +∞)

- Xét hàm số

Ta có: D = R \ {1}

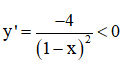∀ x ∈ D.

⇒ Hàm số nghịch biến trên từng khoảng (-∞ ; 1) và (1 ; +∞).

Bài 2 trang 45 SGK

Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số

y = x⁴ – 2x² + 2

Lời giải:

a) Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:

Quy tắc 1:

1. Tìm tập xác định.

2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

1. Tìm tập xác định.

2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.

3. Tính f"(x) và f"(xi)

4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.

Nếu f"(xi) < 0 thì xi là điểm cực đại.

b) Xét hàm số y = x⁴ – 2x² + 2, ta có:

y' = 4x³ – 4x = 4x(x² – 1)

y' = 0 ⇔ 4x(x² – 1) = 0 ⇔ x = 0; x = ±1

y" = 12x² – 4

Dựa vào Quy tắc 2, ta có:

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.

y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.

Bài 3 trang 45 SGK

Nêu cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số. Áp dụng để tìm các đường tiệm cận của hàm số

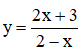
Lời giải:

a)

- Cách tìm tiệm cận ngang:

+ Tính các giới hạn  

+ Nếu hoặc  thì y = y₀ là tiệm cận ngang của đồ thị hàm số.

- Cách tìm tiệm cận đứng:

Đường thẳng x = x₀ là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

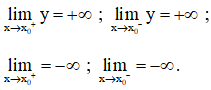
b) Xét hàm số:

⇒ Đồ thị có tiệm cận đứng là x = 2.

⇒ Đồ thị có tiệm cận ngang là y = -2.

Bài 4 trang 45 SGK

Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Lời giải:

Hàm số y = f(x)

Các bước khảo sát hàm số:

1. Tìm tập xác định của hàm số

2. Sự biến thiên

- Xét chiều biến thiên:

   + Tính đạo hàm y'

   + Tìm các điểm tại đó y' bằng 0 hoặc không xác định

   + Xét dấu của đạo hàm y' và suy ra chiều biến thiên của hàm số.

- Tìm cực trị

- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có)

- Lập bảng biến thiên.

3. Vẽ đồ thị của hàm số

Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.

Bài 5 trang 45 SGK

Cho hàm số y = 2x² + 2mx + m – 1 có đồ thị là (C_m), m là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 1.

b) Xác định m để hàm số:

    i) Đồng biến trên khoảng (-1 ; +∞);

    ii) Có cực trị trên khoảng (-1 ; +∞).

c) Chứng minh rằng (C_m) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Lời giải:

a) Với m = 1 ta được hàm số: y = 2x² + 2x

- TXĐ: D = ℝ

- Sự biến thiên:

+ Chiều biến thiên: y' = 4x + 2

y' = 0 ⇔ 4x + 2 = 0 ⇔ x = −1/2

+ Bảng biến thiên:

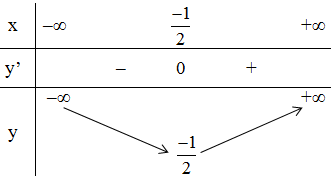
Kết luận: Hàm số nghịch biến trên (-∞ ; −1/2), đồng biến trên (−1/2 ; +∞).

Đồ thị hàm số có điểm cực tiểu là (−1/2 ; −1/2)

- Đồ thị:

Ta có: 2x² + 2x = 0 ⇔ 2x(x + 1) = 0

⇒ x = 0; x = -1

+ Giao với Ox: (0 ; 0); (-1 ; 0)

+ Giao với Oy: (0 ; 0)

Đồ thị hàm số đi qua điểm (-2 ; 4), (1 ; 4)

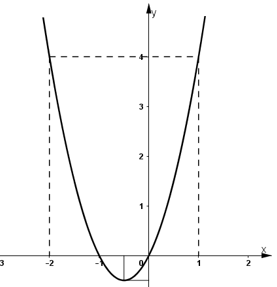
b) Xét hàm số y = 2x² + 2mx + m – 1

y' = 4x + 2m = 2(2x + m)

y' = 0 ⇒ x = −m/2

Ta có bảng xét biến thiên:

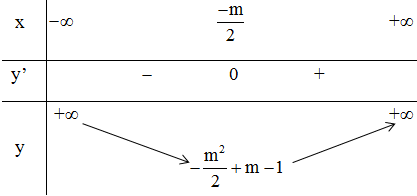
Từ bảng biến thiên ta thấy:

i) Hàm số đồng biến trên khoảng (-1 ; +∞)

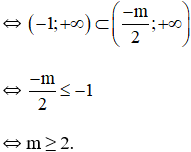
Vậy với m ≥ 2 thì hàm số đã cho đồng biến trên khoảng (-1 ; +∞).

ii) Hàm số có cực trị trên khoảng (-1 ; +∞)

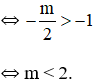
Vậy với m < 2 thì hàm số đã cho có cực trị trên khoảng (-1 ; +∞).

c) Nhận thấy: 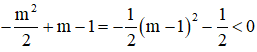với mọi m.

Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi m.

Dựa vào bảng biến thiên suy ra đường thẳng y = 0 (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).

Bài 6 trang 45 SGK

Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số

f(x) = -x³ + 3x² + 9x + 2

b) Giải phương trình f'(x – 1) > 0.

c) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x₀, biết rằng f'(x₀) = -6.

Lời giải:

a) Khảo sát hàm số f(x) = -x³ + 3x² + 9x + 2

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

f'(x) = -3x² + 6x + 9

f'(x) = 0 ⇔ -3x² + 6x + 9 = 0 ⇔ x = -1; x = 3

+ Giới hạn:

+ Bảng biến thiên:

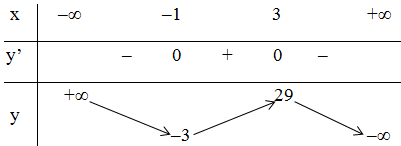
Kết luận:

Hàm số đồng biến trên (-1 ; 3)

Hàm số nghịch biến trên (-∞ ; -1) và (3 ; +∞).

Hàm số đạt cực đại tại x = 3, y_CĐ = 29.

Hàm số đạt cực tiểu tại x = -1; y_CT = -3.

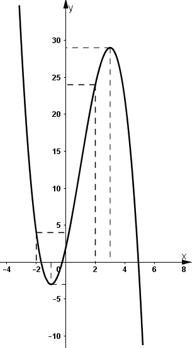
- Đồ thị:

+ Giao với trục tung tại (0 ; 2).

+ Đi qua các điểm (-2 ; 4); (2 ; 24).

b) f’(x) = -3x² + 6x + 9.

⇒ f’(x – 1) = -3(x – 1)2 + 6.(x – 1) + 9.

Ta có: f'(x – 1) > 0

⇔ -3(x – 1)² + 6(x – 1) + 9 > 0

⇔ -3(x² – 2x + 1) + 6x – 6 + 9 > 0

⇔ -3x² + 6x – 3 + 6x – 6 + 9 > 0

⇔ -3x² + 12x > 0

⇔ -x² + 4x > 0

⇔ x(4 – x) > 0 ⇔ 0 < x < 4

c) Ta có: f"(x) = -6x + 6

Theo bài: f"(x₀) = -6 ⇔ -6x₀ + 6 = -6 ⇔ x₀ = 2

Tại y0 = 2, f’(2) = -3.22 + 6.2 + 9 = 9 ; f(2) = -23 + 3.22 + 9.2 + 2 = 24.

⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ y₀ = 2 là:

y = 9(x – 2) + 24 hay y = 9x + 6.

Bài 7 trang 46 SGK

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

y = x³ + 3x² + 1

b) Dựa vào đồ thị (C), biện luận số nghiệm phương trình sau theo m:

c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).

Lời giải:

a) Khảo sát hàm số y = x³ + 3x² + 1

- TXĐ: D = ℝ

- Sự biến thiên:

+ Chiều biến thiên:

y' = 3x² + 6x = 3x(x + 2)

y' = 0 ⇔ x = 0 hoặc x = -2

+ Giới hạn:

+ Bảng biến thiên:

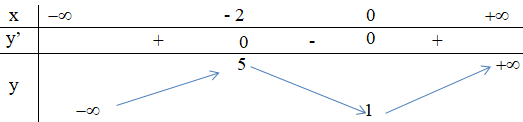
Kết luận:

Hàm số đồng biến trên các khoảng (-∞ ; -2) và (0 ; +∞).

Hàm số nghịch biến trên khoảng (-2 ; 0).

Hàm số đạt cực tiểu tại x = 0; y_CT = 1.

Hàm số đạt cực đại tại x = -2; y_CĐ = 5.

- Đồ thị:

+ Giao với Oy: (0 ; 1).

+ Đồ thị (C) đi qua điểm (-3 ; 1), (1 ; 5).

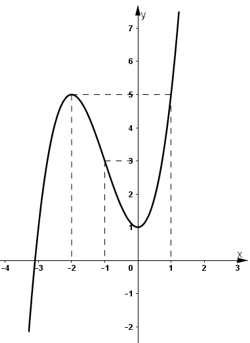
b) Số nghiệm của phương trình x³ + 3x² + 1 = m/2.

 bằng số giao điểm của đồ thị (C) và đường thẳng y = m/2.

Từ đồ thị ta có:

+ Đường thẳng cắt đồ thị tại 1 điểm khi và chỉ khi:

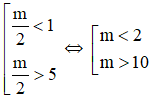
Khi đó phương trình có 1 nghiệm.

+ Để đường thẳng cắt đồ thị tại 2 điểm phân biệt khi và chỉ khi:

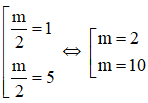
Khi đó phương trình có hai nghiệm phân biệt.

+ Với  ⇔ 2 < m < 10.

Khi đó đường thẳng y = m/2 cắt đồ thị hàm số tại 3 điểm

Do đó phương trình có ba nghiệm phân biệt.

c) Điểm cực đại A(-2 ; 5) và điểm cực tiểu B(0 ; 1).

Vtcp của đường thẳng AB:  = (0 + 2; 1 − 5) = (2 ; -4) = 2(1 ; -2)

Suy ra VTPT của AB là

Đường thẳng AB đi qua A(-2 ; 5) và có VTPT nên có phương trình:

2(x + 2) + 1( y – 5) = 0 hay 2x + y – 1 = 0

Vậy phương trình đường thẳng đi qua điểm cực tiểu và điểm cực đại của đồ thị (C) là: 2x + y – 1 = 0.

Bài 8 trang 46 SGK

Cho hàm số: f(x) = x³ – 3mx² + 3(2m – 1)x + 1 (m là tham số).

a) Xác định m để hàm số đồng biến trên tập xác định.

b) Với giá trị nào của tham số m thì hàm số có một cực đại và một cực tiểu?

c) Xác định m để f"(x) > 6x.

Lời giải:

a) TXĐ: D = R

f'(x) = 3x² – 6mx + 3(2m – 1)

Hàm số đồng biến trên R

⇔ f’(x) > 0 với ∀ x ∈ R.

⇔ Δ_f'(x) = (3m)² – 3.3(2m – 1) ≤ 0

⇔ 9m² – 18m + 9 ≤ 0

⇔ 9.(m – 1)² ≤ 0

⇔ (m – 1)² = 0

⇔ m = 1.

b) Hàm số có một cực đại và một cực tiểu

⇔ phương trình f’(x) = 0 có 2 nghiệm phân biệt.

⇔ Δ_f'(x) = 9(m – 1)² > 0

⇔ m ≠ 1

c) Ta có: f"(x) = 6x – 6m

f"(x) > 6x ⇔ 6x – 6m > 6x

⇔ -6m > 0 ⇔ m < 0

Bài 9 trang 46 SGK

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

b) Viết phương tình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình f"(x) = 0.

c) Biện luận theo tham số m số nghiệm của phương trình: x⁴ – 6x² + 3 = m.

Lời giải:

a) Khảo sát hàm số

- TXĐ: D = ℝ

- Sự biến thiên:

+ Chiều biến thiên:

f'(x) = 2x³ – 6x = 2x(x² – 3)

f'(x) = 0 ⇔ 2x(x² – 3) = 0 ⇔ x = 0; x = ±√3

+ Giới hạn tại vô cực:

+ Bảng biến thiên:

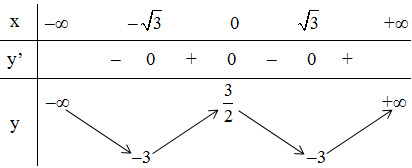
Kết luận: Hàm số đồng biến trên (-√3 ; 0) và (√3 ; +∞).

Hàm số nghịch biến trên (-∞ ; -√3) và (0 ; √3).

Hàm số đạt cực đại tại x = 0, y_CĐ = 

Hàm số đạt cực tiểu tại x = ; y_CT = -3.

- Đồ thị:

+ Đồ thị hàm số nhận trục tung là trục đối xứng.

+ Đồ thị cắt trục tung tại (0 ; 1,5).

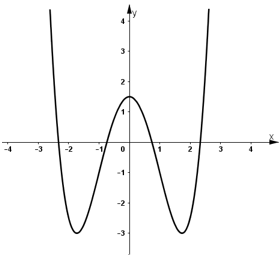
b) Ta có: f"(x) = 6x² – 6 = 6(x² – 1)

f"(x) = 0 ⇔ 6(x² – 1) ⇔ x = ±1 ⇔ y(±1) = -1

Phương trình tiếp tuyến của (C) tại (-1; -1) là:

y = f'(-1)(x + 1) – 1 y = 4x + 3

Phương trình tiếp tuyến của (C) tại (1; -1) là:

y = f'(1)(x – 1) – 1 y = -4x + 3

c) Ta có: x⁴ – 6x² + 3 = m (*)

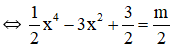
Số nghiệm của phương trình (*) chính bằng số giao điểm của• đồ thị (C) và đường thẳng (d) y = m/2.

Từ đồ thị (C) nhận thấy:

•m/2 < - 3 ⇔ m < -6

Suy ra đường thẳng (d) không cắt đồ thị (C)

Phương trình vô nghiệm.

•m/2 = -3 ⇔ m = -6

Suy ra đường thẳng (d) cắt đồ thị (C) tại hai điểm

Phương trình có 2 nghiệm phân biệt.

•-3 < m/2 < 3/2 ⇔ -6 < m < 3

Suy ra đường thẳng (d) cắt (C) tại 4 điểm phân biệt

Phương trình có 4 nghiệm phân biệt.

•m/2 = 3/2 ⇔ m = 3

Suy ra đường thẳng (d) cắt (C) tại ba điểm

Phương trình có 3 nghiệm phân biệt.

•m/2 > 3/2 ⇔ m > 3

Suy ra đường thẳng (d) cắt (C) tại hai điểm

Phương trình có hai nghiệm phân biệt.

Vậy:

•m < - 6 thì phương trình vô nghiệm.

•m = - 6 hoặc m > 3 thì PT có 2 nghiệm.

•m = 3 thì PT có 3 nghiệm phân biệt.

•- 6 < m < 3 thì PT có 4 nghiệm phân biệt.

Bài 10 trang 46 SGK

Cho hàm số

y = -x⁴ + 2mx² – 2m + 1 (m tham số)

có đồ thị là (C_m).

a) Biện luận theo m số cực trị của hàm số.

d) Với giá trị nào của m thì (C_m) cắt trục hoành?

c) Xác định để (C_m) có cực đại, cực tiểu.

Lời giải:

a) y' = -4x³ + 4mx = 4x(m – x²)

y' = 0 ⇔ 4x(m – x²) = 0 ⇔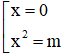

y’’ = -12x² + 4m.

- Nếu m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.

Mà y’’(0) = 4m < 0

⇒ x = 0 là điểm cực đại và là cực trị duy nhất của hàm số.

- Nếu m > 0 thì phương trình (1) có 2 nghiệm phân biệt khác 0 nên phương trình y’= 0 có 3 nghiệm

⇒ hàm số có 3 cực trị.

b)

- Xét m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.

Ta có bảng biến thiên:

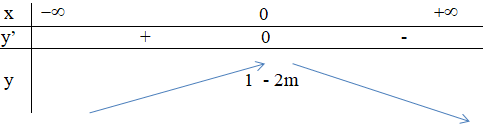
(C_m) cắt trục hoành ⇔ 1 – 2m ≥ 0

⇔ m ≤  (thỏa mãn với mọi m ≤ 0) (1)

- Xét m > 0, phương trình y’ = 0 có 3 nghiệm 0;  

Ta có bảng biến thiên:

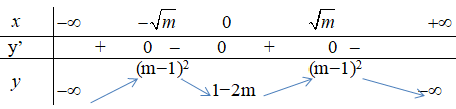
(C_m) cắt trục hoành ⇔ (m – 1)² ≥ 0 (thỏa mãn với mọi m) (2)

Kết hợp (1) và (2) suy ra (C_m) cắt trục hoành với mọi m ∈ R.

c) Dựa vào bảng biến thiên phần b) ta có:

(C_m) có cực đại, cực tiểu ⇔ m > 0.

Bài 11 trang 46 SGK

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

b) Chứng minh rằng với mọi giá trị của đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.

c) Xác định m sao cho độ dài MN nhỏ nhất.

d) Tiếp tuyến tại một điểm S bất kì của C cắt hai tiệm cận của C tại P và Q. Chứng minh rằng S là trung điểm của PQ.

Lời giải:

a) Khảo sát hàm số  

- TXĐ: D = R \ {-1}

- Sự biến thiên:

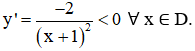
+ Chiều biến thiên:

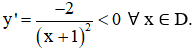
⇒ Hàm số nghịch biến trên các khoảng (-∞ ; -1) và (-1 ; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

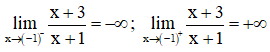
⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.

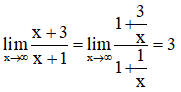
⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

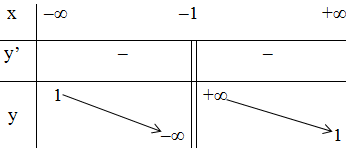
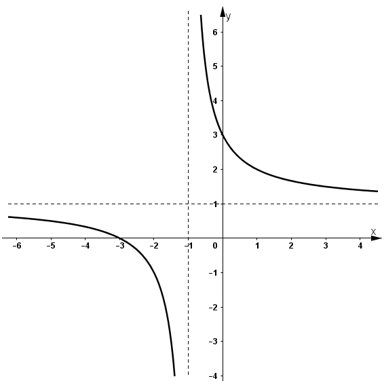
- Đồ thị:

+ Giao với Ox: (-3 ; 0)

+ Giao với Oy: (0 ; 3)

+ Đồ thị hàm số nhận (-1 ; 1) là tâm đối xứng.

b) Phương trình hoành độ giao điểm của (C) và đường thẳng (d) y = 2x + m là:

⇔ (2x + m)(x + 1) = x + 3

⇔ 2x² + mx + 2x + m = x + 3

⇔ 2x² + (m + 1)x + m – 3 = 0 (*)

Để (d) cắt (C) tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt

⇔ (*) có hai nghiệm phân biệt

⇔ Δ = (m + 1)² – 8(m – 3) > 0

⇔ m² – 6m + 25 > 0

⇔ (m – 3)² + 16 > 0

Đúng với ∀ m ∈ R.

Vậy với mọi m ∈ R, (d) cắt (C) tại hai điểm phân biệt MN.

c) Gọi M(x_M; y_M); N(x_N; y_N)

⇒ x_M; x_N là nghiệm của phương trình (*).

Theo hệ thức Vi-et ta có :

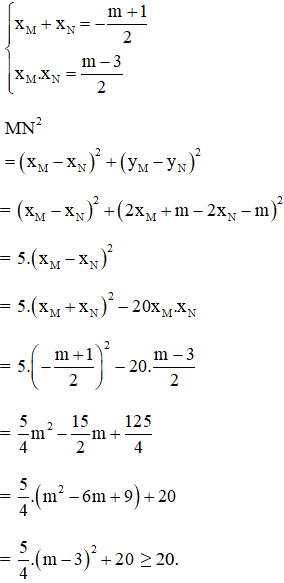
Dấu "=" xảy ra ⇔ m - 3 = 0 ⇔ m = 3

Vậy độ dài MN nhỏ nhất khi m = 3.

d) Gọi 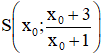 là điểm thuộc (C).

+ Phương trình tiếp tuyến (d) của (C) tại S là:

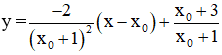
+ Giao điểm của (d) với tiệm cận đứng x = -1 là:

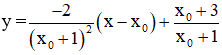
Tại x = -1 thì

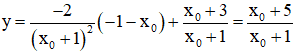
⇒ Giao điểm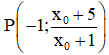

+ Giao điểm của (d) với tiệm cận ngang y = 1:

Tại y = 1

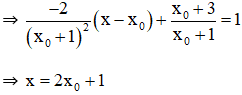
⇒ Giao điểm Q(2x₀ + 1; 1)

Ta có:

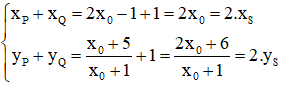
⇒ S là trung điểm PQ (đpcm).

Bài 12 trang 47 SGK

Cho hàm số

a) Giải phương trình f'(sin x) = 0.

b) Giải phương trình f"(cos x) = 0.

c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình f"(x) = 0.

Lời giải:

a) Ta có: f'(x) = x² –  x – 4

⇒ f'(sinx) = sin²x – sin x – 4.

f’(sin x) = 0

⇔ sin²x – sinx –  4 = 0

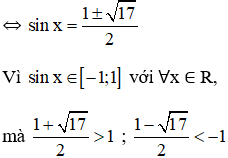
Do đó phương trình vô nghiệm.

b) Ta có: f"(x) = 2x –  1

⇒ f"(cosx) = 2cos x – 1.

    f’’(cos x) = 0

⇔ 2cosx –  1 = 0

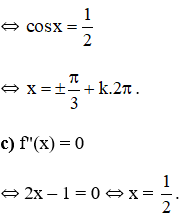
⇒ Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1/2 là:

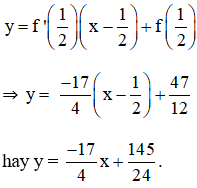
Bài tập trắc nghiệm

Chọn khẳng định đúng trong các bài sau đây.

Câu 1 trang 47 SGK

Số điểm cực trị của hàm số  là:

(A) 1 ;         (B) 0 ;         (C) 3 ;         (D) 2

Lời giải:

- Chọn đáp án B

- Ta có: y' = -x2 - 1 < 0 ∀ x ∈ R

Hàm số luôn nghịch biến trên tập xác định nên không có cực trị.

Câu 2 trang 47 SGK

Số điểm cực đại của hàm số y = x⁴ + 100 là:

(A) 0 ;         (B) 1 ;         (C) 2 ;         (D) 3

Lời giải:

- Chọn đáp án A

- Ta có: y' = 4x³

y’ = 0 ⇔ 4x³ = 0 ⇔ x = 0.

Ta có bảng biến thiên:

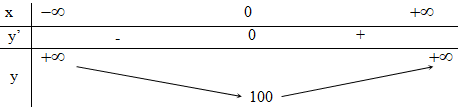
Dựa vào bảng biến thiên thấy hàm số không có cực đại.

Câu 3 trang 47 SGK

Số đường tiệm cận của đồ thị hàm số là:

(A) 1 ;         (B) 2 ;         (C) 3 ;         (D) 0

Lời giải:

- Chọn đáp án B

- Ta có:

⇒ Đồ thị hàm số có tiệm cận đứng x = -1.

Lại có

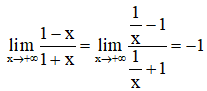
⇒ Đồ thị hàm số có tiệm cận ngang y = -1.

Vậy đồ thị hàm số có hai đường tiệm cận.

Câu 4 trang 47 SGK

Hàm số đồng biến trên:

(A) R;         (B) (-∞ ; 3);         (C) (-3 ; +∞);         (D) R \ {-3}

Lời giải:

- Chọn đáp án D

- TXĐ: D = R \ {-3}

với ∀ x ∈ R.

⇒ Hàm số đồng biến trên từng khoảng (-∞ ; -3) và (-3 ; +∞).

* Lưu ý: Hàm số không đồng biến trên R\{-3} bởi vì:

Lấy x₁ = -4; x₂ = -2 ta có x₁ < x₂ nhưng f(x₁) > f(x₂) (f(x₁₎ = 13 ; f(x₂) = -9).

Hàm số trên chỉ đồng biến trên từng khoảng (-∞ ; -3) và (-3 ; +∞).

Câu 5 trang 47 SGK

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số

(A) Song song với đường thẳng x = 1;

(B) Song song với trục hoành;

(C) Có hệ số góc dương;

(D) Có hệ số gọc bằng -1.

Lời giải:

- Chọn đáp án B

- Ta có: Giả sử (x₀ ; y₀) là điểm cực tiểu của đồ thị hàm số

⇒ f’(x₀) = 0

Phương trình tiếp tuyến tại điểm tại điểm (x₀; y₀) là:

y = f’(x₀)(x – x₀) + y₀ = y₀ song song với trục hoành.

Sách giáo khoa liên quan