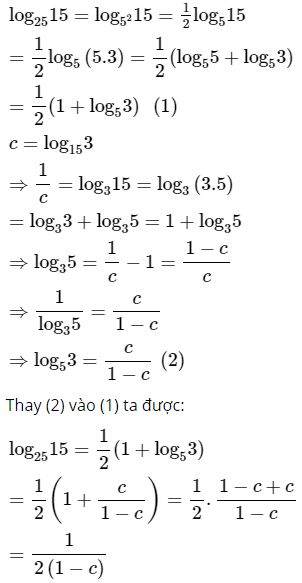Câu hỏi 1 trang 61 SGK
Tìm x để:
![]()
Lời giải:
a) 2x = 8 ⇔ 2x = 23 ⇔ x = 3.
Vậy x = 3.
b) 2x = 1/4 ⇔ 2x = 2(-2) ⇔ x = -2.
Vậy x = -2.
c) 3x = 81 ⇔ 3x = 34 ⇔ x = 4.
Vậy x = 4.
d) 5x = 1/125 ⇔ 5x = 5(-3) ⇔ x = -3.
Vậy x = -3.
Câu hỏi 2 trang 62 SGK
a) Tính ![]()
b) Có các số x, y nào để 3x = 0, 2y = -3 hay không?
Lời giải:
a)
b) Không có số x, y nào để 3x = 0, 2y = -3 vì 3x > 0,2y > 0 với mọi x, y.
Câu hỏi 3 trang 62 SGK
Hãy chứng minh các tính chất:
Với a, b là các số dương và a ≠ 1 thì:
loga1 = logaa = 1
alogab = b, loga(aα) =α
Lời giải:
Ta có:
a0 = 1 ⇔ 0 = loga1
a1 = a ⇔ 1 = logaa
• Đặt α = logab
Từ định nghĩa logarit ta có α = logab nên b = aα = alogab
⇒ alogab = b
• Đặt logaaα = b.
Theo định nghĩa aα = ab nên α = b.
Vậy logaaα = b = α.
Câu hỏi 4 trang 63 SGK
Tính 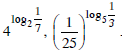
Lời giải:
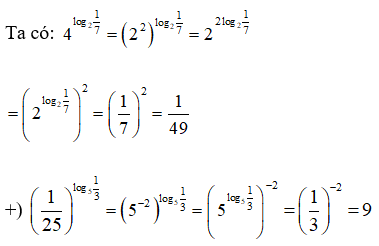
Câu hỏi 5 trang 63 SGK
Cho b1 = 23, b2 = 25.
Tính log2b1 + log2b2; log2(b1b2) và so sánh các kết quả.
Lời giải:
log2b1 + log2b2 = log223 + log225 = 3log22+ 5log22= 3 + 5 = 8.
log2(b1b2) = log2(23.25 ) = log2(2(3+5))= log2(28) = 8log22 = 8.
Vậy log2b1 + log2b2 = log2(b1b2).
Câu hỏi 6 trang 64 SGK
Tính ![]()
Lời giải:
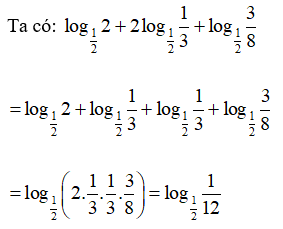
Câu hỏi 7 trang 64 SGK
Tính Cho b1 = 25, b2 = 23. Tính log2b1 − log2b2, ![]() và so sánh các kết quả.
và so sánh các kết quả.
Lời giải:
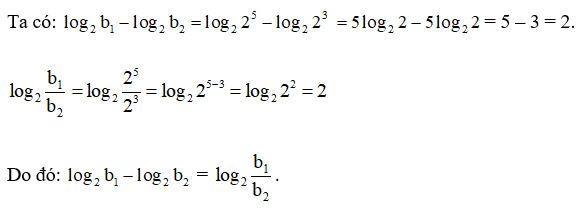
Câu hỏi 8 trang 65 SGK
Cho a = 4, b = 64, c = 2. Tính logab, logca, logcb.
Tìm một hệ thức liên hệ giữa ba kết quả thu được.
Lời giải:
logab = log464 = log443 = 3.
logca = log24 = log222 = 2.
logcb = log264 = log226 = 6.
3 . 2 = 6 ⇒ logab . logca = logcb
Bài 1 trang 68 SGK
Không sử dụng máy tính, hãy tính:
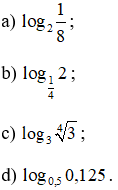
Lời giải:
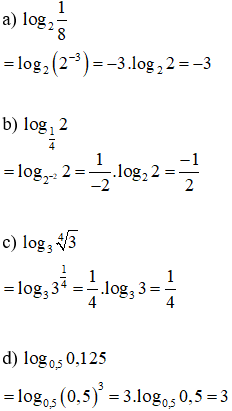
Kiến thức áp dụng
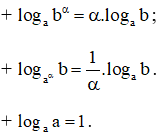 |
Bài 2 trang 68 SGK
Tính:
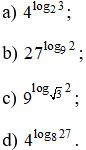
Lời giải:
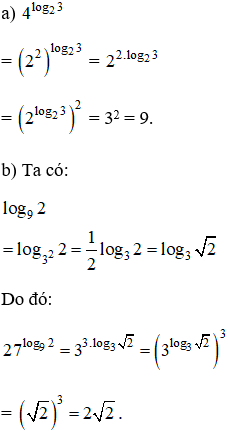
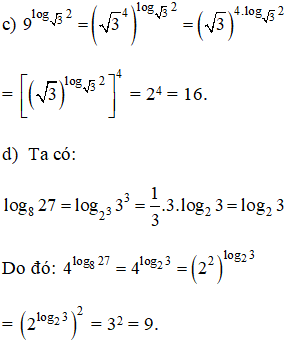
Kiến thức áp dụng
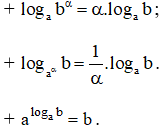 |
Bài 3 trang 68 SGK
Rút gọn biểu thức:
a) log36.log89.log62;
b) logab2+loga2b4
Lời giải:
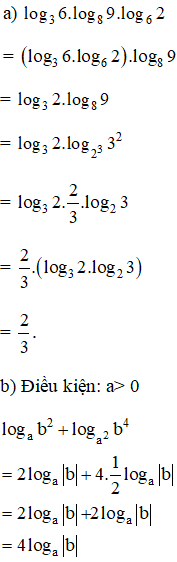
Kiến thức áp dụng
| Với a > 0; a ≠ 1 và b > 0 ta có:
|
Bài 4 trang 68 SGK
So sánh các cặp số sau:
a) log35 và log74;
b) log0,32 và log53;
c) log210 và log530.
Lời giải:
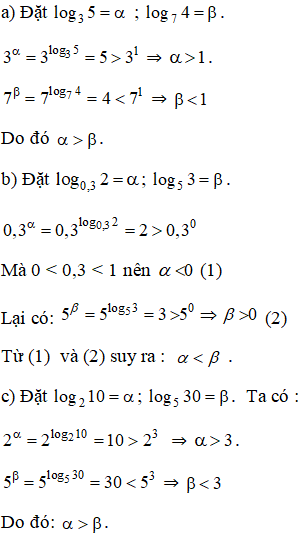
Kiến thức áp dụng
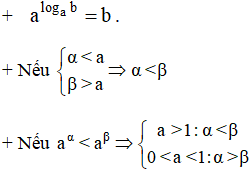 |
Bài 5 trang 68 SGK
a) Cho a = log303; b = log305. Hãy tính log301350 theo a, b.
b) Cho c = log153. Hãy tính log2515 theo c.
Lời giải:
a) Ta có: 1350 = 30.32.5
log301350 = log30(30.32.5)
= log3030 + log3032 + log305
= 1 + 2log303 + log305
= 1 + 2a + b
Vậy log301350 = 1 + 2a + b.
b)
Cách 1:
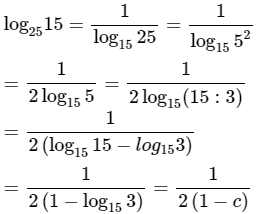
Cách 2: