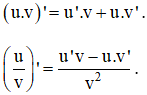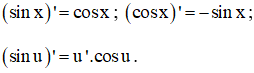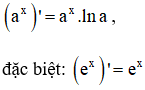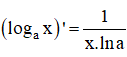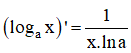Câu hỏi 1 trang 71 SGK
Cho biết năm 2003, Việt Nam có 80 902 400 người và tỉ lệ tăng dân số là 1,47%. Hỏi năm 2010 Việt Nam sẽ có bao nhiêu người, nếu tỉ lệ tăng dân số hằng năm không đổi?
Lời giải:
Áp dụng Ví dụ 1, ta thấy số dân năm 2003 là P = 80 902 400 người
Tỉ lệ tăng dân số là r = 1,47% = 0,0147
Từ năm 2003 đến năm 2010 là 7 năm nên n = 7.
Vậy năm 2010 Việt Nam sẽ có số người là:
80 902 400 . (1 + 0,0147)7 = 89 603 511,14 ≈ 89 603 511 người.
Câu hỏi 2 trang 71 SGK
Trong các hàm số sau đây, hàm số nào là hàm số mũ ? Với cơ số bao nhiêu?
a) y = (√3)x;
b) y = 5x/3;
c) y = x-4;
d) y = 4-x.
Lời giải:
Các hàm số mũ là:
• y = (√3)x với cơ số là √3.
• y = 5x/3 = (51/3)x với cơ số là 51/3.
• y = 4-x = (4−1)x = (1/4)x với cơ số là 4-1 = 1/4.
Hàm số y = 4-x không phải là hàm số mũ.
Câu hỏi 3 trang 75 SGK
Tìm đạo hàm của hàm số ![]()
Lời giải:
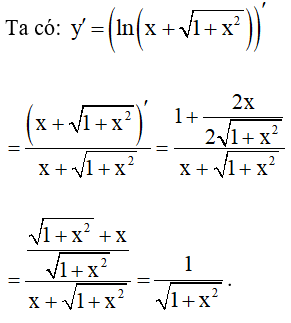
Câu hỏi 4 trang 77 SGK
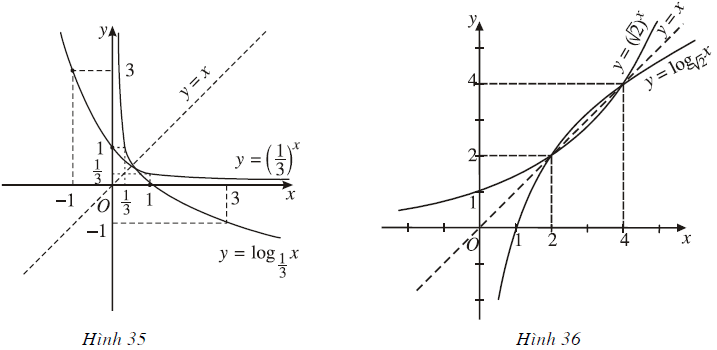
Nêu nhận xét về mối liên hệ giữa đồ thị của các hàm số trên Hình 35 và Hình 36.
Lời giải:
Nhận xét: Đồ thị của các hàm số trên Hình 35 và Hình 36 đối xứng nhau qua đường thẳng y = x.
Bài 1 trang 77 SGK
Vẽ đồ thị của các hàm số:
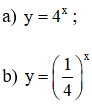
Lời giải:
a) Hàm số y = 4x
- Tập xác định: D = R.
- Sự biến thiên:
+ y' = 4x.ln4 > 0 ∀ x ∈ R.
⇒ Hàm số đồng biến trên R.
![]()
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
![]()
+ Bảng biến thiên:
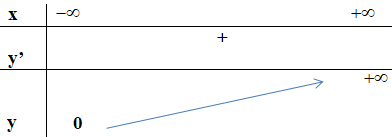
- Đồ thị:
+ Đồ thị hàm số đi qua (0 ; 1) và (1 ; 4).
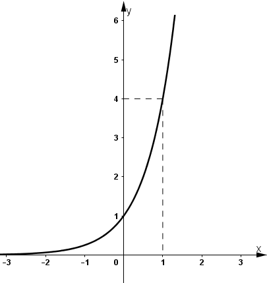
b) Hàm số ![]()
- Tập xác định: D = R.
- Sự biến thiên:
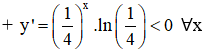
⇒ Hàm số nghịch biến trên R.
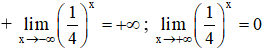
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
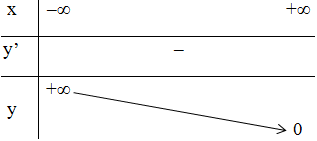
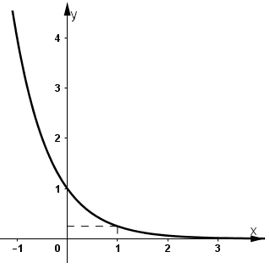
- Đồ thị hàm số:
+ Đồ thị hàm số đi qua (0 ; 1) và ![]()
Kiến thức áp dụng
| Hàm số y = ax có đạo hàm tại mọi x và: (ax)' = ax.lna + Với a > 1 thì ln a > 0 + Với 0 < a < 1 thì ln a < 0 |
Bài 2 trang 77 SGK
Tính đạo hàm của các hàm số:
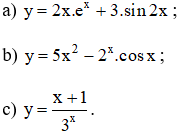
Lời giải:
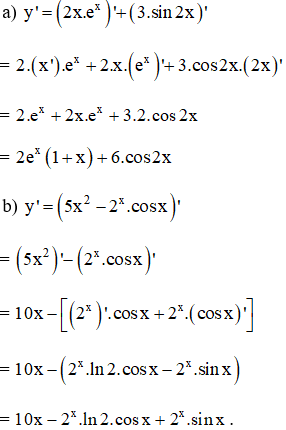
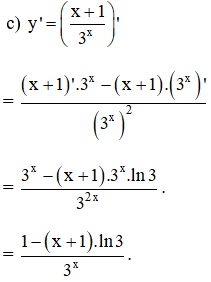
Kiến thức áp dụng
| + Đạo hàm của một tích hoặc một thương:
+ Đạo hàm của hàm số lượng giác:
+ Đạo hàm của hàm số mũ:
|
Bài 3 trang 77 SGK
Tìm tập xác định của các hàm số:
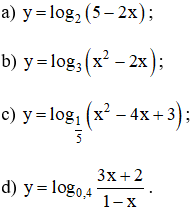
Lời giải:
a) Hàm số y = log2(5 – 2x) xác định
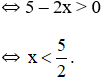
Vậy tập xác định của hàm số là ![]()
b) Hàm số y = log3(x2 – 2x) xác định
⇔ x2 – 2x > 0
⇔ x(x – 2) > 0
⇔ x < 0 hoặc x > 2.
Vậy tập xác định của hàm số là D = (-∞; 0) ∪ (2; +∞)
c) Hàm số ![]() xác định
xác định
⇔ x2 – 4x + 3 > 0
⇔ (x – 1)(x – 3) > 0
⇔ x > 3 hoặc x < 1.
Vậy tập xác định của hàm số là D = (-∞ ; 1) ∪ (3 ; +∞)
d) Hàm số ![]() xác định
xác định
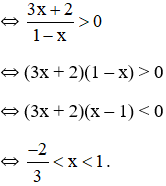
Vậy tập xác định của hàm số là ![]()
Kiến thức áp dụng
| Với a > 0 và a ≠ 1 thì hàm số y = logaf(x) xác định khi f(x) có nghĩa và f(x) > 0. |
Bài 4 trang 78 SGK
Vẽ đồ thị của các hàm số:
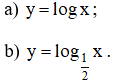
Lời giải:
a) Hàm số y = logx
- Tập xác định: D = (0 ; +∞).
- Chiều biến thiên:
+ Đạo hàm:
![]()
⇒ Hàm số đồng biến trên D.
![]()
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
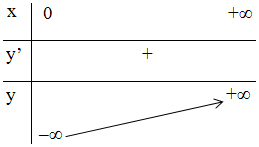
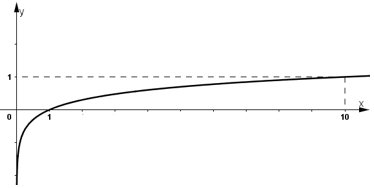
- Đồ thị hàm số:
+ Đồ thị hàm số đi qua (1 ; 0) và (10 ; 1).
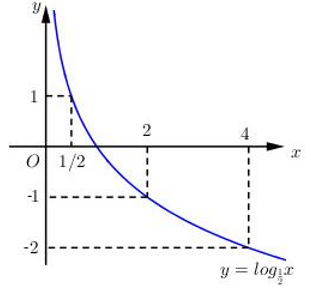
b) Hàm số ![]()
- Tập xác định: D = (0 ; +∞).
- Chiều biến thiên:
+ Đạo hàm:
Suy ra hàm số nghịch biến trên (0 ; +∞).
+ Giới hạn:
![]()
Suy ra x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
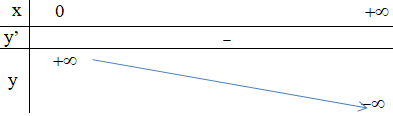
- Đồ thị:
+ Đồ thị hàm số đi qua (1 ; 0) và (1/2 ; 1).
Kiến thức áp dụng
| + Đạo hàm của hàm số y = logax:
+ Với a > 0; a ≠ 1 và x > 0 ta có: đạo hàm của hàm số y = logax là:
+ Trục Oy là tiệm cận đứng của đồ thị. + Đồ thị hàm số luôn đi qua điểm (1 ; 0) và (a ; 1) |
Bài 5 trang 78 SGK
Tính đạo hàm của các hàm số:
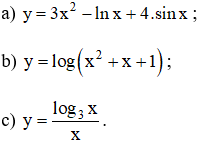
Lời giải:
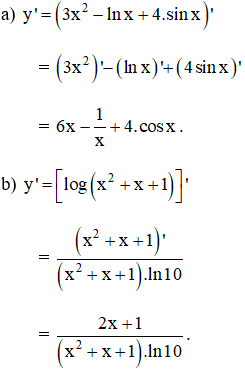
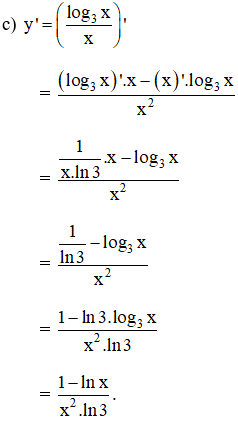
Kiến thức áp dụng
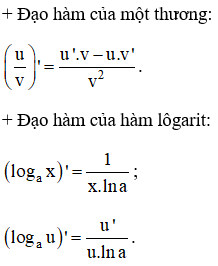 |