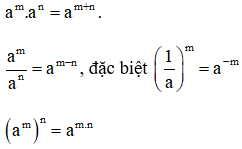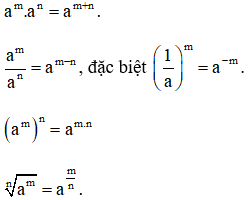Câu hỏi 1 trang 49 SGK
Tính 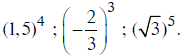
Lời giải:
(1,5)4 = 5,0625
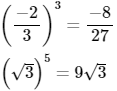
Câu hỏi 2 trang 50 SGK
Dựa vào đồ thị của các hàm số y = x3 và y = x4 (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x3 = b và x4 = b.
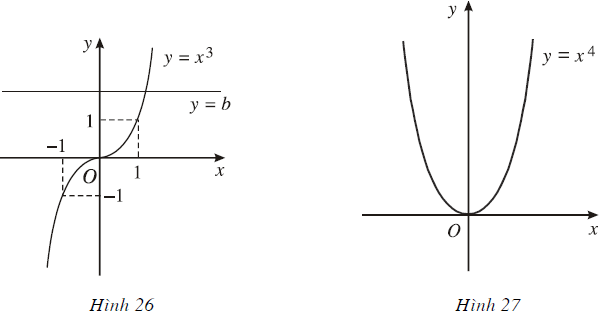
Lời giải:
* Số nghiệm của phương trình x3 = b là số giao điểm của hai đồ thị hàm số y = b và y = x3.
Dựa vào Hình 26 ta có: đồ thị hàm số y = x3 luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x3 = b luôn có nghiệm duy nhất với mọi b.
* Số nghiệm của phương trình x4 = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x4.
Dựa và Hình 27 ta có:
+ Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.
+ Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0 , 0), vậy phương trình (1) có nghiệm duy nhất x = 0.
+ Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biệt, vậy phương trình (1) có hai nghiệm phân biệt.
Câu hỏi 3 trang 52 SGK
Chứng minh tính chất n√a.n√b = n√ab.
Lời giải:
Đặt n√a = x; n√b = y. Khi đó: xn = a; yn = b.
Ta có a.b = xn.yn = (xy)n
Vậy xy là căn bậc n của ab.
Suy ra n√ab = x.y = n√a.n√b
Câu hỏi 4 trang 54 SGK
Hãy nhắc lại các tính chất của lũy thừa với số mũ nguyên dương.
Lời giải:
Với a, b là các số thực; m, n là các số nguyên dương, ta có:
* Các tính chất về đẳng thức:
1. am. an = a(m+n)
2. am : an = a(m-n) (m ≥ n).
3. (am)n = am.n
4. (a/b)m = am/bm (b ≠ 0)
5. (ab)m = am.bm
* Các tính chất về bất đẳng thức
Với a > 1 thì am > an ⇔ m > n.
Với 0 < a < 1 thì am > an ⇔ m < n.
Với 0 < a < b thì am > bm.
Câu hỏi 5 trang 55 SGK
Rút gọn biểu thức 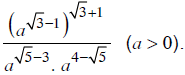
Lời giải:
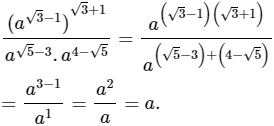
Câu hỏi 6 trang 55 SGK
So sánh các số 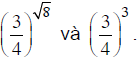
Lời giải:
Ta có:
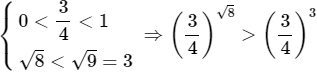
Bài 1 trang 55 SGK
Tính:
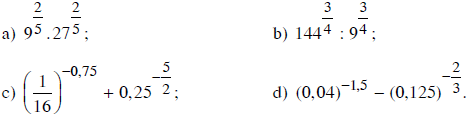
Lời giải:
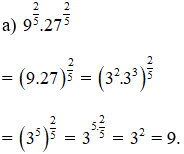
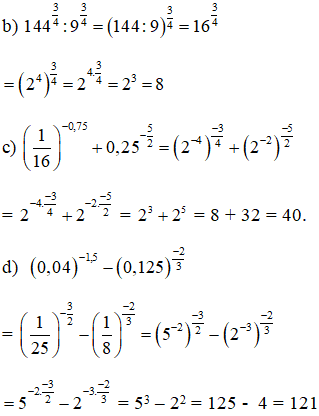
Kiến thức áp dụng
| Với a là số thực dương; m, n là các số thực tùy ý ta có:
|
Bài 2 trang 55 SGK
Cho a, b là những số thực dương. Viết các biểu thức dưới dạng lũy thừa với số mũ hữu tỉ:

Lời giải:
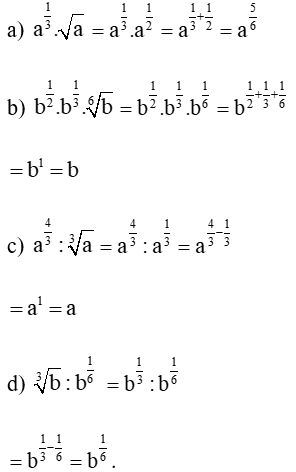
Kiến thức áp dụng
| Với a là số thực dương; m, n là các số thực tùy ý ta có:
|
Bài 3 trang 56 SGK
Viết các số sau theo thứ tự tăng dần:

Lời giải:
a) Ta có:
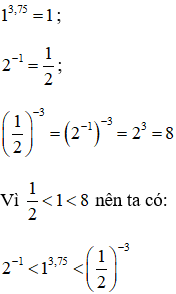
b) Ta có:
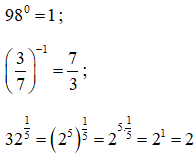
Vì ![]() nên ta có:
nên ta có: 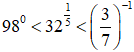 .
.
Bài 4 trang 56 SGK
Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
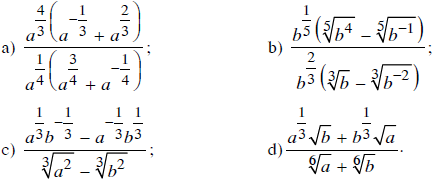
Lời giải:
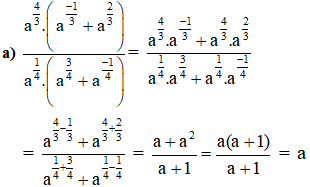
(Với a>0).
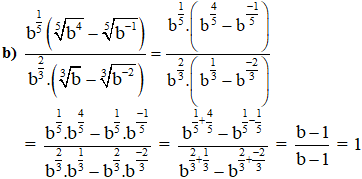
(Với điều kiện b>0; b≠1).
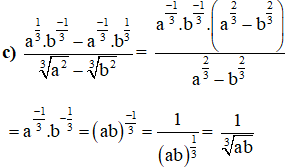
(Với điều kiện a≠b; a,b>0).
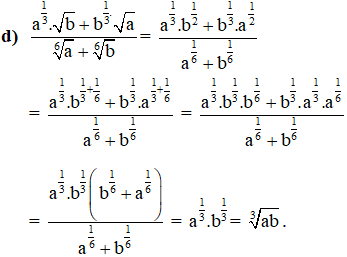
(Với a,b>0).
Bài 5 trang 56 SGK
Chứng minh rằng:

Lời giải:
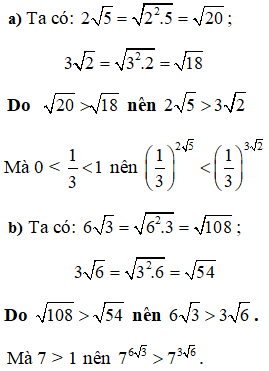
Kiến thức áp dụng
| Cho hai số thực m, n thỏa mãn m > n, khi đó: •0 < a < 1 thì am < an; •a > 1 thì am > an. |