Câu hỏi 1 trang 4 SGK
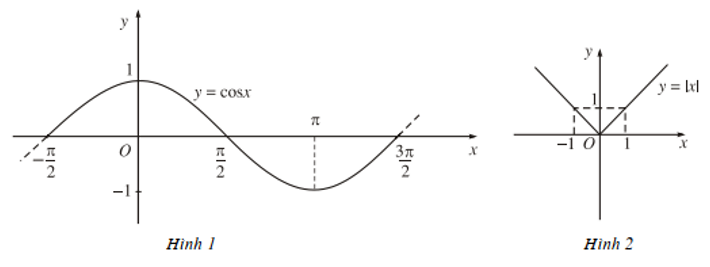
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [−π/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞).
 Lời giải:
Lời giải:
+ Hình 1: Hàm số y = cosx trên đoạn [−π/2; 3π/2]:
- Các khoảng tăng: [−π/2; 0], [π; 3π/2] (do đồ thị hàm số đi lên trong các khoảng đó, nghĩa là khi x tăng thì y cũng tăng).
- Khoảng giảm: [0; π] (do đồ thị hàm số đi xuống trong khoảng đó, nghĩa là khi x tăng thì y giảm).
+ Hình 2: Hàm số y = |x| trên khoảng (–∞; +∞):
- Khoảng tăng: [0; +∞) (do đồ thị hàm số đi lên trong khoảng đó, nghĩa là khi x tăng thì y cũng tăng).
- Khoảng giảm (–∞; 0] (do đồ thị hàm số đi xuống trong khoảng đó, nghĩa là khi x tăng thì y giảm).
Câu hỏi 2 trang 5 SGK
Xét các hàm số sau và đồ thị của chúng:
a) y = −x2/2 (H.4a)
b) y = 1/x (H.4b)
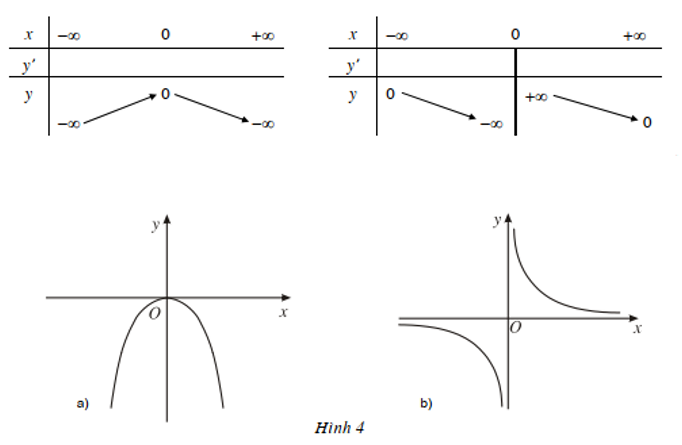
Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng. Từ đó hãy nêu nhận xét về mối quan hệ giữa sự đồng biến, nghịch biến của hàm số và dấu của đạo hàm.
Lời giải:
a) Hàm số y = −x2/2 có đạo hàm y' = –x, y' = 0 khi x = 0.
Trên khoảng (–∞; 0), đạo hàm y' mang dấu +, đồ thị hàm số đi lên; trên khoảng (0; +∞), đạo hàm mang dấu –, đồ thị hàm số đi xuống. Ta có bảng biến thiên như sau:
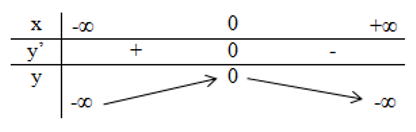
b) Hàm số y = 1x xác định trên ℝ\{0} có đạo hàm là y' = −1/x2 < 0 với mọi x ∈ ℝ\{0}.
Do đó, trên các khoảng (–∞; 0), (0; +∞) đạo hàm y' đều mang dấu –, đồ thị hàm số đi xuống. Ta có bảng biến thiên như sau:
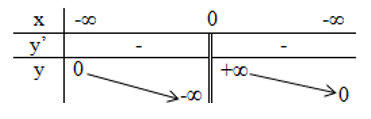
* Nhận xét: Cho hàm số y = f(x) có đạo hàm trên K.
+ Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
+ Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
Câu hỏi 3 trang 7 SGK
Khẳng định ngược lại với định lí trên có đúng không? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không?
Lời giải:
Xét hàm số y = x3 có đạo hàm y’ = 3x2 ≥ 0 với mọi số thực x và hàm số đồng biến trên toàn bộ R. Vậy khẳng định ngược lại với định lý trên chưa chắc đúng hay nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó không nhất thiết phải dương (âm) trên đó.
Bài tập 1 trang 9 SGK
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 4 + 3x – x2;
b) y = 1/3x3 + 3x2 – 7x - 2;
c) y = x4 – 2x2 + 3;
d) y = -x3 + x2 – 5.
Lời giải:
a) Tập xác định: D = ℝ
Ta có: y' = 3 – 2x
y’ = 0 ⇔ 3 – 2x = 0 ⇔ x = 3/2
Ta có bảng biến thiên:
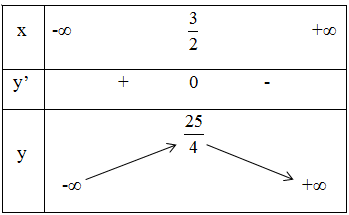
Vậy hàm số đồng biến trong khoảng (–∞ ; 3/2) và nghịch biến trong khoảng (3/2 ; + ∞).
b) Tập xác định: D = ℝ
Ta có: y' = x2 + 6x – 7
y' = 0 ⇔ x2 + 6x – 7 ⇔ x = -7 hoặc x = 1
Ta có bảng biến thiên:
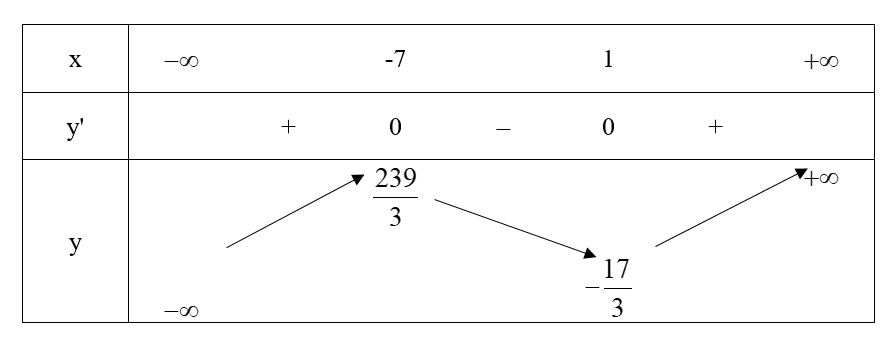
Vậy hàm số đồng biến trong các khoảng (-∞ ; -7) và (1 ; +∞); nghịch biến trong khoảng (-7 ; 1).
c) Tập xác định: D = ℝ
Ta có: y'= 4x3 – 4x
y' = 0 ⇔ 4x3 – 4x = 0 ⇔ 4x.(x – 1)(x + 1) = 0 ⇔ x = 0 hoặc x = 1 hoặc x = -1
Bảng biến thiên:
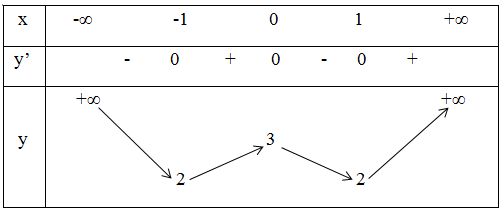
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -1) và (0 ; 1); đồng biến trong các khoảng (-1 ; 0) và (1; +∞).
d) Tập xác định: D = ℝ
Ta có: y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ x = 0 hoặc x = 2/3
Bảng biến thiên:
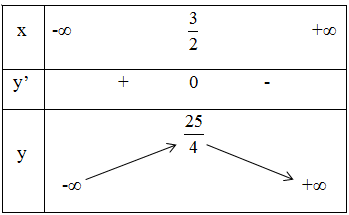
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (23; +∞), đồng biến trong khoảng (0 ; 23).
Bài tập 2 trang 10 SGK
Tìm các khoảng đơn điệu của các hàm số:
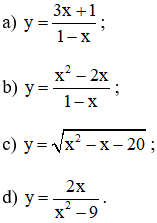
Lời giải:
a) Tập xác định: D = R \ {1}
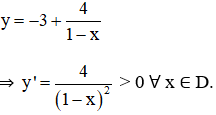
y' không xác định tại x = 1
Bảng biến thiên:
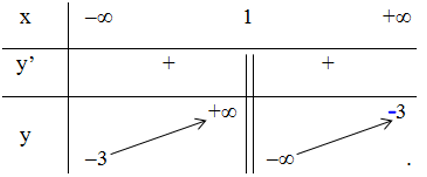
Vậy hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞).
b) Tập xác định: D = R \ {1}
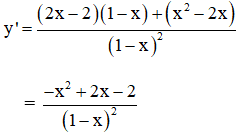
y’ < 0 với ∀ x ∈ D (vì -x2 + 2x – 2 < 0).
y' không xác định tại x = 1
Bảng biến thiên:
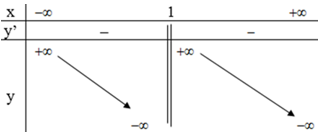
Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞)
c) Tập xác định: D = (-∞ ; -4] ∪ [5; +∞)
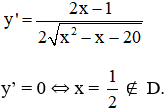
y' không xác định tại x = -4 và x = 5
Bảng biến thiên:

Vậy hàm số nghịch biến trong khoảng (-∞; -4); đồng biến trong khoảng (5; +∞).
d) Tập xác định: D = R \ {±3}
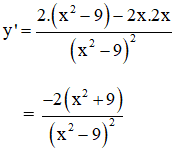
Vì x2 ≥ 0 ∀ x ⇒ x2 + 9 > 0 ∀ x ⇔ -2(x2 + 9) < 0
Mà (x2 – 9)2 > 0 ∀ x ∈ D
Suy ra: y’ < 0 với ∀ x ∈ D.
y' không xác định tại x = ±3
Bảng biến thiên:
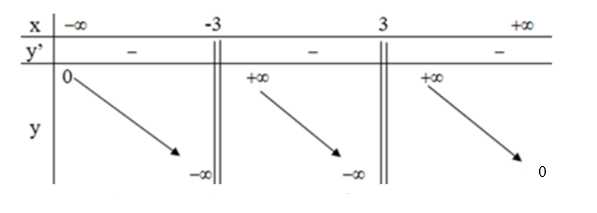 Vậy hàm số nghịch biến trong các khoảng (-∞ ; -3); ( -3; 3) và (3; +∞ ).
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -3); ( -3; 3) và (3; +∞ ).
Bài tập 3 trang 10 SGK
Chứng minh rằng hàm số ![]() đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Lời giải:
TXĐ: D = R
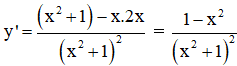
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 – x2 < 0
⇔ x2 > 1
⇔ x ∈ (-∞ ; -1) ∪ (1 ; +∞).
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 1 – x2 > 0
⇔ x2 < 1
⇔ x ∈ (-1; 1).
Vậy hàm số đồng biến trên khoảng (-1; 1) và nghịch biến trên các khoảng (-∞; -1) và (1; +∞).
Bài tập 4 trang 10 SGK
Chứng minh rằng hàm số ![]() đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Lời giải:
TXĐ: D = [0; 2]
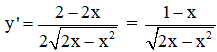
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Bài tập 5 trang 10 SGK
Chứng minh các bất đẳng thức sau:
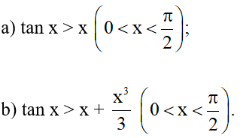
Lời giải:
a) Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ = 1/cosx2 – 1 = tan2x > 0 với mọi số thực x.
Suy ra hàm số đồng biến trên khoảng (0; π/2)
Do đó: f(x) > f(0) với mọi x ∈ (0; π/2)
Lại có: f(0) = tan 0 – 0 = 0
Khi đó: tan x – x > 0 với mọi x ∈ (0; π/2)
tan x > x với mọi x ∈ (0; π/2) (đpcm).
b) Xét hàm số y = g(x) = tanx – x – x3/3 trên (0; π/2)
Ta có: g'(x) = 1 cos2x − 1 − x2 = tan2x − x2 = (tan x – x)(tan x + x)
Theo kết quả câu a) ta có: tan x – x > 0 với mọi x ∈ (0; π/2) , hơn nữa tan x + x > 0 với mọi x ∈ (0; π/2)
Do đó: g'(x) > 0 ∀ x ∈ (0; π/2)
Suy ra y = g'(x) đồng biến trên (0; π/2)
=> g(x) > g(0) với mọi x ∈ (0; π/2)
Lại có: g(0) = tan 0 – 0 – 03/3 = 0
Do đó: g(x) > 0 với mọi x ∈ (0; π/2)
Hay tanx – x – x3/3 > 0 với mọi x ∈ (0; π/2)
Khi đó: tan > x + x3/3 với mọi x ∈ (0; π/2) (đpcm).



































