(Trang 104)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Hai đường tròn cắt nhau - Hai đường tròn tiếp xúc nhau - Hai đường tròn không giao nhau. - Tiếp điểm | Nhận biết các vị trí tương đối của hai đường tròn. |
• Nguyệt thực là hiện tượng Mặt Trăng bị bóng của Trái Đất che khuất toàn bộ (nguyệt thực toàn phần) hay một phần (H.5.30). Do Mặt Trăng và bóng Trái Đất được xem là có dạng hình tròn nên nguyệt thực cho ta một hình ảnh thực tế về vị trí tương đối của hai đường tròn. Em có thể cắt ra hai hình tròn bằng giấy để mô phỏng hiện tượng nguyệt thực. Nhưng trước hết hãy tìm hiểu về vị trí tương đối của hai đường tròn.
• Sau đây, khi nói hai đường tròn mà không có giải thích gì thêm, ta hiểu đó là hai đường tròn phân biệt.

Hình 5.30
1 HAI ĐƯỜNG TRÒN CẮT NHAU
Tìm hiểu hai đường tròn cắt nhau
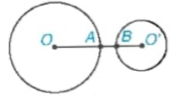
HĐ1 Cho hình 5.31, trong đó giả sử O'A < OA. Ta có OA - O'A < OO' < OA + O'A.
Hãy vẽ hai đường tròn (O; OA) và (O'; O'A) và cho biết hai đường tròn đó có mấy điểm chung?
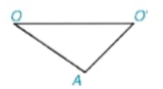
Hình 5.31
Nếu hai đường tròn có đúng hai điểm chung thì ta nói đó là hai đường tròn cắt nhau. Hai điểm chung gọi là hai giao điểm của chúng.
Nhận xét
Từ HĐ1 ta thấy hai đường tròn (O; R) và (O'; R') cắt nhau khi
R - R'< OO' < R+ R' (với R > R').
Ví dụ 1 Cho hai điểm O và C sao cho DO – 5 cm. Hãy giải thích tại sao hai đường tròn (O; 4 cm) và (O; 3 cm) cắt nhau.
Hình 5.32
Giải
Đặt R = 4 cm; R' – 3 cm, ta thấy 1 cm < 5 cm < 7 cm, nên R – R' < 00 < R+R'. Do đó, hai đường tròn đã cho cắt nhau.
(Trang 105)
Luyện tập 1
Cho đường tròn (O; 5 cm) và điểm I cách O một khoảng 2 cm. Xác định vị trí tương đối của đường tròn đã cho và đường tròn (l; r) trong mỗi trường hợp sau:
a) r = 4 cm; b) r = 6 cm.
2 HAI ĐƯỜNG TRÒN TIẾP XÚC NHAU
Tìm hiểu hai đường tròn tiếp xúc nhau.
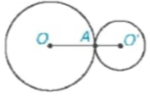
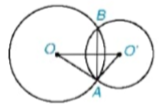
HĐ2 Trên Hình 5.33a, ta có OO' = OA + O'A; trên Hình 5.33b, ta có OO' = OA - O'A. Trong mỗi trường hợp, hãy vẽ hai đường tròn (O, OA) và (O'; O'A) và cho biết hai đường tròn đó có mấy điểm chung?

Hình 5.33
Nếu hai đường tròn có duy nhất một điểm chung thì ta nói đó là hai đường tròn tiếp xúc nhau. Điểm chung gọi là tiếp điểm của chúng.
|
a) Tiếp xúc ngoài |
b) Tiếp xúc trong |
Hình 5.34
Chú ý
Người ta còn phân biệt hai trường hợp: hai đường tròn tiếp xúc ngoài (H.5.34a) và hai đường tròn tiếp xúc trong (H.5.34b).
Nhận xét
1) Từ HĐ2, ta nhận thấy: Hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài khi OO' = R + R', và tiếp xúc trong khi OO' = R - R' (R > R').
2) Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.
Ví dụ 2
Cho hai điểm O và O' sao cho OO' = 5 cm. Giải thích tại sao hai đường tròn (O; 3 cm) và (O'; 2 cm) tiếp xúc với nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài?
Giải
Đặt R = 3 cm và R'= 2 cm, ta thấy 5 cm = 3 cm + 2 cm, nghĩa là OO' = R + R'. Vậy hai đường tròn đã cho tiếp xúc ngoài với nhau.
Luyện tập 2
Cho hai điểm O và O' sao cho OO' = 3 cm. Giải thích tại sao hai đường tròn (O, 8 cm) và (O; 5 cm) tiếp xúc với nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài?
(Trang 106)
3 HAI ĐƯỜNG TRÒN KHÔNG GIAO NHAU
Tìm hiểu hai đường tròn không giao nhau
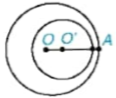
HĐ3 Trên Hình 5.35a, ta có OO' > OA + O'B; trên Hình 5.35b, ta có OO' < OA – O'B.
Trong môi trường hợp, hãy vẽ hai đường tròn (O; OA) và (O';OB) và cho biết hai đường tròn đó có điểm chung nào không.

Hình 5.35
Nếu hai đường tròn không có điểm chung nào thì ta nói đó là hai đường tròn không giao nhau.
Chú ý
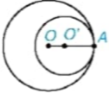
Người ta còn phân biệt hai trường hợp: hai đường tròn ngoài nhau (H.5.36a) và đường tròn này đựng đường tròn kia (H.5.36b). Nhận xét
|
a) Hai đường tròn ngoài nhau |
b) (O) đựng (O') |
Hình 5.36
Nhận xét
Từ HĐ3 ta nhận thấy:
• Hai đường tròn (O; R) và (O'; R') ngoài nhau khi OO' > R+R'.
• Đường tròn (O; R) đựng đường tròn (O'; R') khi R > R' và OO' < R – R'. Đặc biệt, khi O trùng với O' và R≠R' thì ta có hai đường tròn đồng tâm.
Ví dụ 3 Xác định vị trí tương đối của hai đường tròn (O; 3 cm) và (O'; 5 cm), biết rằng OO' > 8 cm.
Giải
Đặt R = 3 cm và R' = 5 cm, ta có OO' = 8 cm > R+ R'.
Vậy (O; 3 cm) và (O'; 5 cm) là hai đường tròn ngoài nhau.
Luyện tập 3
Cho hai điểm O và O' sao cho OO' = 2 cm. Xác định vị trí tương đối của hai đường tròn (O, 5 cm) và (O'; r), biết rằng r < 3 cm.
Thực hành
Để mô phỏng nguyệt thực, em hãy cắt hai hình tròn từ giấy: hình tròn thứ nhất màu sáng tượng trưng cho Mặt Trăng, hình tròn thứ hai màu tối (to hơn và bằng giấy mờ càng tốt) tượng trưng cho bóng Trái Đất. Sắp xếp hai hình tròn đó để:
a) Mô phỏng nguyệt thực một phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?
(Trang 107)
b) Mô phỏng nguyệt thực toàn phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?
Tranh luận
Tròn cho rằng: Nói "hai đường tròn không cắt nhau" cũng có nghĩa là “hai đường tròn không giao nhau". Theo em, Tròn đúng hay sai?
Ta có bảng tổng kết sau:
| Vị trí tương đối của hai đường tròn (O; R) và (O; R') (R ≥ R') | Số điểm chung | Hệ thức giữa OO' với R và R' |
| Hai đường tròn cắt nhau | 2 | R - R' < OO' <R + R' |
| Hai đường tròn tiếp xúc nhau: - Tiếp xúc ngoài - Tiếp xúc trong | 1 | OO' = R + R' OO' = R - R' >0 |
| Hai đường tròng không giao nhau: - (O) và (O') ở ngoài nhau - (O) đựng (O') | 0 | OO' > R + R' OO' < R - R' |
BÀI TẬP
5.24. Hình 5.37 cho thấy hình ảnh của những đường tròn qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và vài cặp đường tròn không giao nhau.

Hình 5.37
5.25. Cho hai điểm O và O' cách nhau một khoảng 5 cm. Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn (O, 3 cm).
a) Đường tròn (O; 3 cm); b) Đường tròn (O'; 1 cm); c) Đường tròn (O'; 8 cm).
5.26. Cho ba điểm thẳng hàng C, A và O'. Với mỗi trường hợp sau, hãy viết hệ thức giữa các độ dài OO', OA và O'A rồi xét xem hai đường tròn (O; OA) và (O'; O'A) tiếp xúc trong hay tiếp xúc ngoài với nhau; vẽ hình để khẳng định dự đoán của mình.
a) Điểm A nằm giữa hai điểm O và O';
b) Điểm O nằm giữa hai điểm A và O';
c) Điểm O' nằm giữa hai điểm A và O.
5.27. Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O') tại C. Chứng minh rằng OB II OC.