(Trang 74)
| Kiến thức, kĩ năng - Giải thích một số hệ thức về cạnh và góc trong tam giác vuông. - Giải tam giác vuông. - Giải quyết một số vấn đề thực tiễn gắn với tỉ số lượng giác của góc nhọn. |
Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P' của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P' dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.
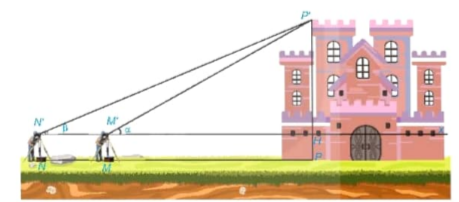
Hình 4.11
1 HỆ THỨC GIỮA CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG
Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
HĐ1 Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).
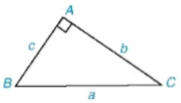
Hình 4.12
a) Viết các tỉ số lượng giác sin, côsin của góc B và góc C theo độ dài các cạnh của tam giác ABC.
b) Tính mỗi cạnh góc vuông b và c theo cạnh huyền a và các tỉ số lượng giác trên của góc B và góc C.
Định lí 1
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Chú ý. Trong tam giác ABC vuông tại A (H.4.12), ta có:
b=a.sin B = a.cos C; c=a.sin C= a.cos B.
(Trang 75)
Ví dụ 1
Một chiếc máy bay bay lên với vận tốc 500 km/h. Đường bay lên tạo với phương nằm ngang một góc 30° (H.4.13). Hỏi sau 1,2 phút, máy bay lên cao được bao nhiêu kilômét theo phương thẳng đứng?
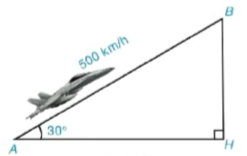
Hình 4.13
Giải
Giả sử trong Hình 4.13, AB là đoạn đường máy bay bay lên trong 1,2 phút thì BH chính là độ cao máy bay đạt được sau 1,2 phút đó.
Ta có 1,2 phút =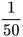 
giờ nên AB = 500.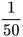=10 (km).
Tam giác ABH vuông tại H, có Â = 30°. Theo Định lí 1, ta có BH = AB.sinA= 10.sin 30°=10.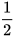
=5 (km).
Vậy sau 1,2 phút, máy bay lên cao được 5 km.
Luyện tập 1
1. Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến số thập phân thứ hai) để nó tạo được với mặt đất một góc "an toàn" 65° (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?
Hình 4.14
2. Một khúc sông rộng khoảng 250 m. Một con đồ chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc ở bằng bao nhiêu độ (làm tròn đến phút)? (H.4.15).
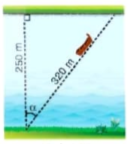
Hình 4.15
2 HỆ THỨC GIỮA HAI CẠNH GÓC VUÔNG
Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
HĐ2 Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, côtang của góc B và góc C theo b, c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.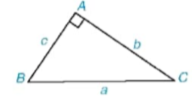
Hình 4.16
(Trang 76)
Định lí 2
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với cô tang góc kể.
Chú ý. Trong tam giác ABC vuông tại A (H.4.16), ta có:
b=c.tan B=c.cot C; c=b.tan C=b.cot B.
Ví dụ 2
Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34° và bóng của một toà tháp trên mặt đất dài 8,6 m (H.4.17). Tính chiều cao của toà tháp đó (làm tròn đến mét).
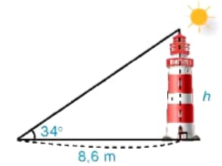
Hình 4.17
Giải
Ta nhận thấy đường cao của tháp đối diện với góc 34° (góc tạo bởi tia nắng mặt trời và bóng của tháp trên mặt đất).
Theo Định lí 2, ta có h = 8,6 . tan 34° ≈ 6 (m).
Vậy chiều cao của tháp là khoảng 6 m.
Luyện tập 2
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm), biết rằng tia nắng mặt trời tạo với mặt đất góc 40° (H.4.18).
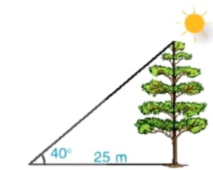
Hình 4.18
3. GIẢI TAM GIÁC VUÔNG
Ví dụ 3 Cho tam giác vuông ABC với các cạnh góc vuông AB = 5, AC = 8 (H.4.19). Hãy tính cạnh BC (làm tròn đến chữ số thập phân thứ nhất) và các góc B, C (làm tròn đến độ).
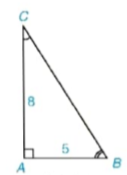
Hình 4.19
Giải. Xét △ABC vuông tại A.
Cách 1. Theo định lí Pythagore, ta có:
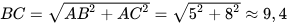
Ta có tan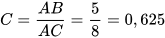 
. Từ đó tìm được 
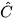= 32°
suy ra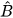 
= 90° - Ĉ ≈ 90°-32° =58°.
(Trang 77)
Cách 2. Sau khi tìm được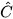 
≈ 32°, ta tính cạnh BC.
Ta có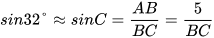 
, suy ra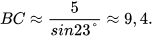 
Luyện tập 3
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
Ví dụ 4 Cho tam giác ABC vuông tại A có AB = 3,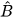 
= 42° (H.4.20). Tính góc C và các cạnh AC, BC (làm tròn đến chữ số thập phân thứ ba).
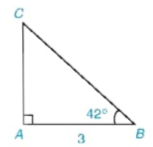
Hình 4.20
Giải
Xét △ABC vuông tại A.
Ta có: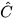 
= 90° – 
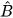= 90° – 42° = 48
AC=AB.tan B = 3.tan 42°≈ 2,701.
Theo định nghĩa các tỉ số lượng giác của góc nhọn, ta có: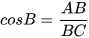
, suy ra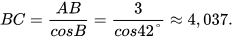 
Giải tam giác vuông là gì?
Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó. Bài toán này gọi là bài toán Giải tam giác vuông.
| Ví dụ 3, Luyện tập 3 và Ví dụ 4 là những bài toán Giải tam giác vuông.
|
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).
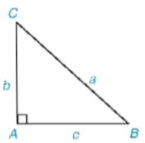
Hình 4.21
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Luyện tập 4
Giải tam giác ABC vuông tại A, biết BC = 9,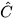 
= 53°.
Vận dụng
Giải bài toán ở tình huống mở đầu với α = 27° và β= 19°.
BÀI TẬP
4.8. Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:
a) a = 21, b = 18; b) b = 10, Ĉ = 30°; c) c = 5, b = 3.
4.9. Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.
|
Hình 4.22 |
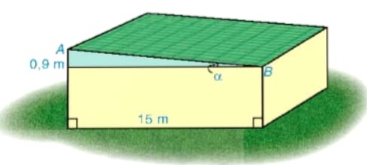
Hình 4.23 |
4.10. Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.
4.11. Tỉnh các góc của hình thoi có hai đường chéo dài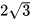 
và 2.
4.12. Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và Â=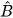 
= 
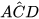= 90°.
a) Kẻ đường cao CE của tam giác ACD. Chứng minh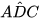 
= 
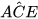. Tính sin của các góc 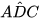, 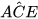và suy ra 
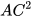= AE . AD. Từ đó tính AC.
b) Tính góc D của hình thang.
4.13. Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tỉnh chiều cao của cây (H.4.24).
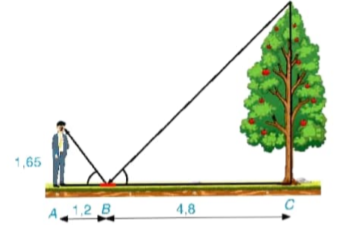
Hình 4.24
(Trang 79)
LUYỆN TẬP CHUNG
Ví dụ 1
Cho tam giác ABC vuông tại A, AB = 5 cm, AC = 12 cm.
a) Tính các tỉ số lượng giác của góc B.
b) Từ kết quả câu a) suy ra các tỉ số lượng giác của góc C.
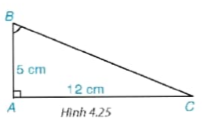
Giải (H.4.25)
a) Xét tam giác ABC vuông tại A. Theo định lí Pythagore, ta có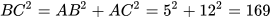 
, suy ra BC = 13 cm.
Ta có: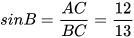 
, 
, 
, 
.
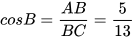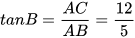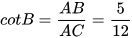b) Do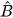 
+ 
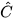= 90° nên 
, 
, 
, 
.
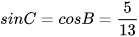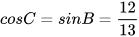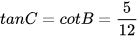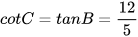Ví dụ 2
Một bức tường đang xây dở có dạng hình thang vuông ABCD, vuông góc ở A và D, AB = 1 m, CD = 4 m, AD = 6 m.
a) Hỏi góc α tạo bởi đường thẳng BC và mặt đất AD có số đo xấp xỉ bằng bao nhiêu (làm tròn đến phút)? (H.4.26)
b) Tính độ dài cạnh BC (làm tròn đến chữ số thập phân thứ nhất).
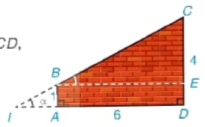
Hình 4.26
Giải
a) Gọi I là giao điểm của hai đường thẳng AD và BC. Qua B kẻ đường thẳng song song với AD (mặt đất) cắt CD ở E thì khi đó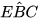 
= 
= α (hai góc đồng vị).
Tứ giác ABED có BE II AD, AB II DE, Â= 90° nên ABED là hình chữ nhật.
Do đó BE = AD = 6 m, EC = CD – ED = 4 – 1 = 3 (m).
Xét △BCE vuông tại E, ta có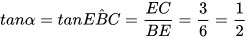 
Từ đó tính được α ≈ 26°34'.
b) Cách 1. Áp dụng định lí Pythagore vào tam giác BEC vuông tại E, ta có:
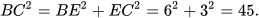Suy ra 
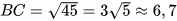(m).
Cách 2. Tam giác BEC vuông tại E nên EC = BC . sin α,
suy ra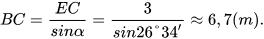 
(Trang 80)
BÀI TẬP
4.14. Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc giữa đường chéo và cạnh 17 cm. Tính sin α, cos α (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).
4.15. Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm,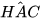 
= 60°. Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).
4.16. Tìm chiều rộng ở của dòng sông trong Hình 4.27 (làm tròn đến m).
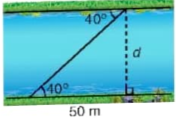
Hình 4.27
4.17. Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
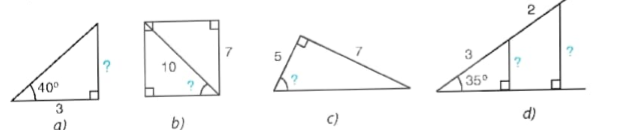
Hình 4.28
4.18. Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và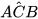 
= 120° (H.4.29). Hãy tính AB giúp bạn.
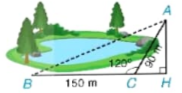
Hình 4.29
4.19. Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tan D = 1,25. Độ dốc của sườn BC, tức là tan C = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
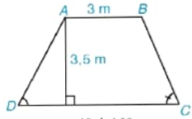
Hình 4.30
4.20. Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).
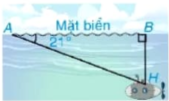
Hình 4.31
a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).
b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?
