(Trang 54)
Bài 9: BIẾN ĐỔI ĐƠN GIẢN VÀ RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
Khái niệm, thuật ngữ
- Phép đưa thừa số ra ngoài hoặc vào trong dấu căn
- Trục căn thức ở mẫu
Kiến thức, kỹ năng
- Thực hiện phép đưa thừa số ra ngoài dấu căn bậc hai, đưa thừa số vào trong dấu căn bậc hai.
- Thực hiện phép trục căn thức ở mẫu.
- Rút gọn biểu thức chứa căn bậc hai
Không sử dụng MTCT, có thể so sánh được hai số: 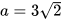 và
và 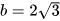 hay không?
hay không?
1. ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN
Cách đưa thừa số ra ngoài dấu căn
HĐ1. Tính và so sánh 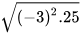 với
với 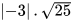 .
.
Nếu a là một số và b là một số không âm thì 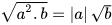 .
.
Chú ý. Phép biến đổi trên gọi là phép đưa thừa số ra ngoài dấu căn.
Ví dụ 1. Viết nhân tử số của biểu thức dưới dấu căn thành tích các luỹ thừa rồi đưa thừa số ra ngoài dấu căn:
a) 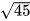 ; b)
; b)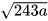 (a≥0).
(a≥0).
Giải:
a) Ta có 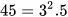 nên
nên 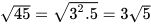 ;
;
b) Ta có 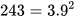 nên
nên 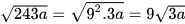
(Trang 55)
Luyện tập 1. Đưa thừa số ra ngoài dấu căn
a) 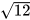 ; b)
; b) 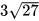 ; c)
; c) 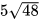
Chú ý. Khi tính toán với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (tức là biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu) như trong ví dụ sau:
Ví dụ 2: Khử mẫu của biểu thức lấy căn 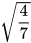 .
.
Giải:
Nhân cả tử và mẫu của biểu thức lấy căn với số 7 và đưa thừa số ra ngoài dấu căn, ta được
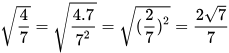
Luyện tập 2: Khử mẫu của biểu thức lấy căn 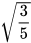 .
.
Tranh luận

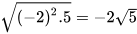
Em có đồng ý với cách làm của Vuông không? Vì sao?
2. ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN
Cách đưa một thừa số vào trong dấu căn
HĐ2: Tính và so sánh
a) 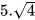 với
với 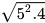 ; b)
; b) 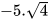 với
với 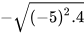 .
.
- Nếu a và b là hai số không âm thì
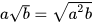 .
. - Nếu a là số âm và b là số không âm thì
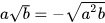
Chú ý: Các phép biến đổi trên gọi là phép đưa thừa số vào trong dấu căn.
(Trang 56)
Ví dụ 3: Đưa thừa số vào trong dấu căn:
a) 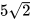 ; b)
; b) 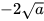 (a≥0)
(a≥0)
Giải
a) 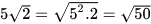 ; b)
; b) 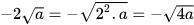
Ví dụ 4: Trả lời câu hỏi trong tình huống mở đầu.
Giải
Ta có 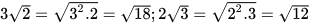
Vì 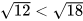 nên
nên 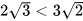
Luyện tập 3: Đưa thừa số vào trong dấu căn:
a) 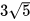 ; b)
; b) 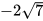
3. TRỤC CĂN THỨC Ở MẪU
Tính toán với các biểu thức có chứa căn ở mẫu thường phức tạp và ta thường tìm cách trục các căn thức ở mẫu (tức là biến đổi biểu thức thành một biểu thức mới không chứa căn ở mẫu).
Cách trục căn thức ở mẫu
HĐ3 Nhân cả tử và mẫu của biểu thức 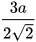 với
với 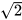 và viết biểu thức nhận được dưới dạng không có căn thức ở mẫu.
và viết biểu thức nhận được dưới dạng không có căn thức ở mẫu.
HĐ4 Cho hai biểu thức 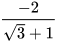 và
và 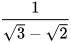 Hãy thực hiện các yêu cầu sau để viết các biểu thức đó dưới dạng không có căn thức ở mẫu:
Hãy thực hiện các yêu cầu sau để viết các biểu thức đó dưới dạng không có căn thức ở mẫu:
a) Xác định biểu thức liên hợp của mẫu.
b) Nhân cả tử và mẫu với biểu thức liên hợp của mẫu.
c) Sử dụng hằng đẳng thức hiệu hai bình phương để rút gọn mẫu của biểu thức nhận được.
(Trang 57)
- Với các biểu thức A, B và B>0, ta có
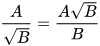 .
. - Với các biểu thức A, B, C mà A≥0, B≥0, A≠B, ta có
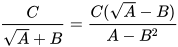 ;
; 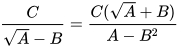
- Với các biểu thức A, B, C mà A≥0, B≥0, A≠B, ta có:
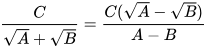 ;
; 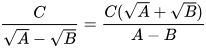
Ví dụ 5: Trục căn thức ở mẫu cửa các biểu thức:
a) 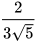 ; b)
; b) 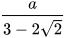 .
.
Giải
a) Nhân cả tử và mẫu của biểu thức đã cho với 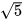 , ta được:
, ta được:
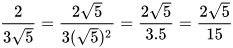
b) Biểu thức liên hợp của mẫu là 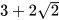 . Nhân cả tử và mẫu của biểu thức đã cho với
. Nhân cả tử và mẫu của biểu thức đã cho với 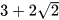 , ta được:
, ta được:
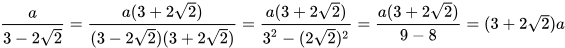
Luyện tập 4: Trục căn thức ở mẫu của các biểu thức sau:
a) 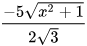 ; b)
; b) 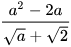 (a≥0, a≠2).
(a≥0, a≠2).
4. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân, chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẫu của biểu thức lấy căn; trục căn thức ở mẫu).
(Trang 58)
Rút gọn biểu thức 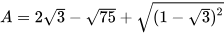
Giải:
Đưa thừa số ra ngoài dấu căn, ta có: 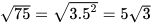 ;
;
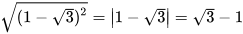 .
.
Do đó 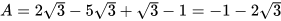
Ví dụ 7:
a) Trục căn thức ở mẫu của các biểu thức: 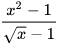 ;
; 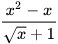 với x>1.
với x>1.
b) Sử dụng kết quả câu a, rút gọn biểu thức 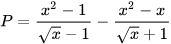 với x>1.
với x>1.
Giải
a) Ta có
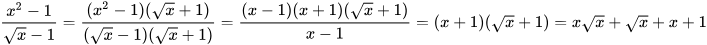
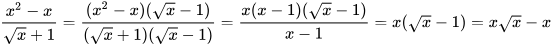 .
.
b) Sử dụng kết quả câu a ta có 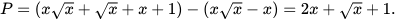
Luyện tập 5: Rút gọn biểu thức sau:
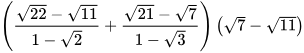
Vận dụng
Trong thuyết tương đối, khối lượng m (kg) của một vật khi chuyển động với tốc độ v(m/s) được cho bởi công thức:
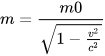
trong đó 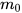 (kg) là khối lượng của vật khi đứng yên, c (m/s) là tốc độ của ánh sáng trong chân không (Theo sác Vật lý đại cương, NXB Giáo dục Việt Nam, 2016).
(kg) là khối lượng của vật khi đứng yên, c (m/s) là tốc độ của ánh sáng trong chân không (Theo sác Vật lý đại cương, NXB Giáo dục Việt Nam, 2016).
(Trang 59)
a) Viết lại công thức tính khối lượng m dưới dạng không có căn thức ở mẫu.
b) Tính khối lượng m theo 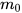 (làm tròn đến chữ số thập phân thứ ba) khi vật chuyển động với vận tốc
(làm tròn đến chữ số thập phân thứ ba) khi vật chuyển động với vận tốc 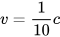
BÀI TẬP
3.17. Đưa thừa số ra ngoài dấu căn:
a)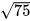 ; b)
; b)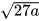 (a≥0);
(a≥0);
c) 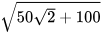 ; d)
; d) 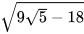
3.18. Đưa thừa số vào trong dấu căn:
a) 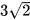 ; b)
; b) 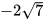 ;
;
c) 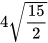 ; d)
; d) 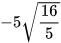
3.19. Khử mẫu trong dấu căn:
a) 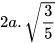 ; b)
; b) 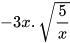 (x>0); c)
(x>0); c) 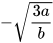 (a≥0, b>0).
(a≥0, b>0).
3.20. Trục căn thức ở mẫu:
a)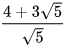 ; b)
; b) 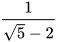 c)
c) 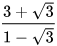 ; d)
; d) 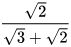
3.21. Rút gon các biểu thức sau:
a) 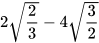 ; b)
; b) 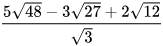 ; c)
; c) 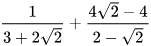
3.22. Rút gọn biểu thức 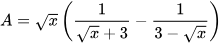 (x≥0, x≠9)
(x≥0, x≠9)



































