(Trang 60)
Bài 10: CĂN BẬC BA VÀ CĂN THỨC BẬC BA
Khái niệm, thuật ngữ - Căn bậc ba
- Căn bậc ba
- Căn thức bậc ba
Kiến thức, kĩ năng
- Nhận biết căn bậc ba của một số thực.
- Tính giá trị đúng, gần đúng của căn bậc ba của một số bằng máy tính cầm tay.
- Nhận biết căn thức bậc ba của một biểu thức đại số.
Căn bậc hai của một số thực (dương) có một vai trò quan trọng trong đời sống và toán học. Căn bậc hai của số thực a không âm là các số thực x thoả mãn điều kiện x² = a. Trong bài học này, các em sẽ được làm quen với khái niệm căn bậc ba, một khái niệm tương tự khái niệm căn bậc hai.
1. CĂN BẬC BA
Căn bậc ba của một số thực
HĐ1. Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu "?" trong bảng sau bằng các giá trị thích hợp.
| x | V=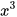 |
| 2 | 8 |
| ? | 27 |
| ? | 64 |

Tổng quát, ta định nghĩa:
Căn bậc ba của số thực a là số thực x thoả mãn x³ = a.
Chú ý. Mỗi số a đều có duy nhất một căn bậc ba. Căn bậc ba của số a được kí hiệu là 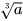 . Trong kí hiệu
. Trong kí hiệu 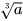 , số 3 được gọi là chỉ số của căn. Phép tìm căn bậc ba của một số gọi là phép khai căn bậc ba.
, số 3 được gọi là chỉ số của căn. Phép tìm căn bậc ba của một số gọi là phép khai căn bậc ba.
Ví dụ 1:
a) Chứng tỏ rằng 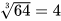 . b) Tính
. b) Tính 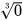 và
và 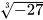
Giải. a) Vì 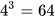 nên
nên 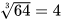
b) Vì 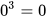 nên
nên 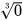 =0. Vì
=0. Vì  = -27 nên
= -27 nên 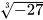 = -3
= -3
Nhận xét. Từ định nghĩa căn bậc ba, ta có 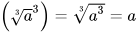 với mọi số thực a. Do đó có thể giải Ví dụ 1 như sau:
với mọi số thực a. Do đó có thể giải Ví dụ 1 như sau: 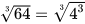 =4
=4
(Trang 61)
Luyện tập 1: Tính: a) 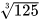 ; b)
; b)  ; c)
; c)
Tính căn bậc ba của một số bằng máy tính cầm tay
Ta có thể sử dụng MTCT thích hợp để tính căn bậc ba của một số. Chẳng hạn, để tính 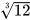 và
và 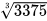 ta làm như sau:
ta làm như sau:
| Phép tính | Bấm các phím | Kết quả |
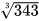 |  | 7 |
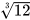 |  | 2,289428485 |
Chú ý. Màn hình MTCT chỉ hiển thị được một số hữu hạn chữ số nên các kết quả là số thập phân vô hạn (tuần hoàn hay không tuần hoàn) đều được làm tròn, chẳng hạn: 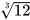 ≈2,289428485
≈2,289428485
Ví dụ 2:
Sử dụng MTCT, tính  rồi làm tròn kết quả đến chữ số thập phân thứ hai.
rồi làm tròn kết quả đến chữ số thập phân thứ hai.
Giải. Bấm các phím  , màn hình hiện kết quả 1,481248034. Làm tròn kết quả đến chữ số thập phân thứ hai ta được
, màn hình hiện kết quả 1,481248034. Làm tròn kết quả đến chữ số thập phân thứ hai ta được 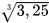 ≈1,48
≈1,48
Luyện tập 2
Sử dụng MTCT, tính 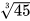 và làm tròn kết quả với độ chính xác 0,005.
và làm tròn kết quả với độ chính xác 0,005.
Thử thách nhỏ
 Có thể xếp 125 khối lập phương đơn vị (có cạnh bằng 1 cm) thành một khối lập phương lớn được không nhỉ?
Có thể xếp 125 khối lập phương đơn vị (có cạnh bằng 1 cm) thành một khối lập phương lớn được không nhỉ?
2. CĂN THỨC BẬC BA
Nhận biết căn thức bậc ba
Tương tự như căn thức bậc hai, ta có định nghĩa sau:
Căn thức bậc ba là biểu thức có dạng 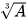 , trong đó A là một biểu thức đại số.
, trong đó A là một biểu thức đại số.
(Trang 62)
Chú ý
- Tương tự căn bậc ba của một số, ta cũng có
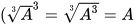 (A là một biểu thức).
(A là một biểu thức). - Để tính giá trị của
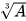 tại những giá trị cho trước của biển, ta thay các giá trị cho trước của biến vào căn thức rồi tính giá trị của biểu thức số nhận được.
tại những giá trị cho trước của biển, ta thay các giá trị cho trước của biến vào căn thức rồi tính giá trị của biểu thức số nhận được.
Ví dụ 3: Tính giá trị của căn thức 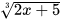 tại:
tại:
a) x=60; b) x=-6,5.
Giải
a) Với x=60 ta có 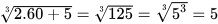
b) Với x= -6,5 ta có 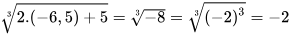
Ví dụ 4: Rút gọn biểu thức 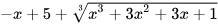 .
.
Giải
Ta có 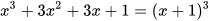 <- hằng đẳng thức lập phương của một tổng
<- hằng đẳng thức lập phương của một tổng
Do đó 
Luyện tập 3
a) Tính giá trị của căn thức 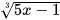 tại x=0 và tại x=-1,4.
tại x=0 và tại x=-1,4.
b) Rút gọn biểu thức 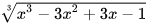 .
.
BÀI TẬP
3.23. Tính:
a) 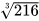 ; b)
; b)  ; c)
; c) 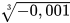 ; d)
; d) 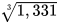 .
.
3.24. Sử dụng MTCT, tính các căn bậc ba sau đây (làm tròn kết quả đến chữ số thập phân thứ hai):
a) 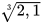 ; b)
; b) 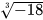 ; c)
; c) 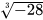 ; d)
; d) 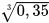 .
.
3.25. Một người thợ muốn làm một thùng tôn hình lập phương có thể tích bằng 730 dm³.
Em hãy ước lượng chiều dài cạnh thùng khoảng bao nhiêu dm?
3.26. Rút gọn các biểu thức sau:
a) 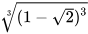 ; b)
; b) 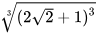 ; c)
; c) 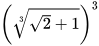
3.27. Rút gọn rồi tính giá trị của biểu thức 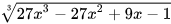 tại x=7
tại x=7
(Trang 63)
LUYỆN TẬP CHUNG
Ví dụ 1: Rút gọn biểu thức 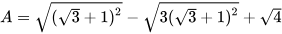
Giải:
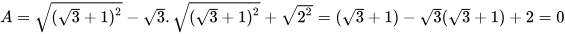
Ví dụ 2:
Cho biểu thức  với x>1
với x>1
a) Rút gọn P.
b) Sử dụng kết quả câu a, tính giá trị của P khi x=101.
Giải
a) 
b) Khi x=101 thì 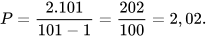
Ví dụ 3
Người ta cần làm một thùng hình lập phương bằng bìa cứng không có nắp trên và có thể tích 216 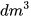 để đựng đồ. Tính diện tích bìa cứng cần dùng để làm thùng đựng đó (coi diện tích các mép nối là không đáng kể).
để đựng đồ. Tính diện tích bìa cứng cần dùng để làm thùng đựng đó (coi diện tích các mép nối là không đáng kể).
Giải
Gọi x (dm, x > 0) là độ dài cạnh của thùng hình lập phương cần làm.
Ta có: x³ = 216, suy ra x = 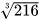 = 6 (dm).
= 6 (dm).
Vì thùng đựng không có nắp nên thùng gồm 4 mặt bên và 1 mặt đáy, mỗi mặt là một hình vuông cạnh 6 dm. Do đó diện tích bìa cứng cần dùng là
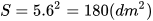
(Trang 64)
BÀI TẬP
3.28.Rút gọn các biểu thức sau:
a) 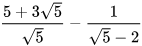 ; b)
; b)  ;
;
c) 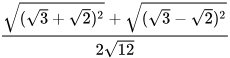 ; d)
; d) 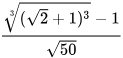 .
.
3.29. Tính giá trị của các biểu thức sau:
a)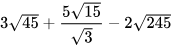 ; b)
; b) 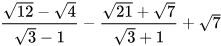 ;
;
c) 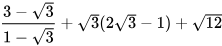 ; d)
; d) 
3.30. Giả sử lực F của gió khi thổi theo phương vuông góc với bề mặt cánh buồm của một con thuyền tỉ lệ thuận với bình phương tốc độ của gió, hệ số tỉ lệ là 30. Trong đó, lực F được tính bằng N (Newton) và tốc độ được tính bằng m/s.
a) Khi tốc độ của gió là 10 m/s thì lực F là bao nhiêu Newton?
b) Nếu cánh buồm chỉ có thể chịu được một áp lực tối đa là 12 000 N thì con thuyền đó có thể đi được trong gió với tốc độ gió tối đa là bao nhiêu?
3.31. Rút gọn các biểu thức sau:
a)  ; b)
; b) 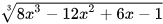
(Trang 65)
BÀI TẬP CUỐI CHƯƠNG III:
A. TRẮC NGHIỆM
3.32. Căn bặc hai của 4 là
A. 2. B.-2. C. 2 và -2. d. 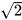 và
và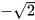
3.33. Căn bậc hai số học của 49 là
A. 7. B.-7. C. 7 và -7. d. 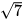 và
và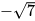
3.34. Rút gọn biểu thức  ta được
ta được
A. 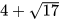 . B.
. B. 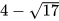 . C.
. C. 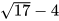 . d.
. d. 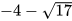 .
.
3.35. Độ dài đường kính (mét) của hình tròn có diện tích 4 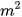 sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng
sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng
A. 2,26. B. 2,50. C. 1,13. D. 1,12.
3.36. Một vật rơi tự do từ độ cao 396,9 m. Biết quãng đường chuyển động S (mét) của vật phụ thuộc vào thời gian t (giây) bởi công thức S = 4,9t². Vật chạm đất sau
A. 8 giây. B. 5 giây. C. 11 giây. D. 9 giây.
B. TỰ LUẬN
3.37. Không sử dụng MTCT, tính giá trị của biểu thức
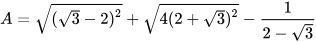 .
.
3.38. Cho biểu thức  (x>0, x≠4).
(x>0, x≠4).
a) Rút gọn biểu thức A.
b) Tính giá trị của A tại x = 14.
3.39. Biết rằng nhiệt lượng toả ra trên dây dẫn được tính bởi công thức Q = I²Rt, trong đó Q là nhiệt lượng tính bằng đơn vị Joule (J), R là điện trở tính bằng đơn vị Ohm (Ω), là cường độ dòng điện tính bằng đơn vị Ampe (A), t là thời gian tính bằng giây (s). Dòng điện chạy qua một dây dẫn có R = 10 Ω trong thời gian 5 giây.
a) Thay dấu "?" trong bảng sau bằng các giá trị thích hợp.
| I (A) | 1 | 1,5 | 2 |
| Q (J) | ? | ? | ? |
b. Cường độ dòng điện là bao nhiêu Ampe để nhiệt lượng tỏa ra trên dây dẫn đạt 800J?