(Trang 66)
Trong chương này ta xét các tỉ số hai độ dài hai cạnh của một tam giác vuông. Ta sẽ thấy các tỉ số này đặc trưng cho độ lớn của hai góc nhọn của tam giác vuông đó. Nói cách khác, nếu biết được mỗi tỉ số này, ta sẽ biết được độ lớn của hai góc nhọn.
Bài 11: Tỉ số lượng giác của góc nhọn
Khái niệm, thuật ngữ
- Tỉ số lượng giác của góc nhọn
- Sin, côsin, tang, côtang
Kiến thức, kỹ năng
- Nhận biết sin, côsin, tang, côtang của góc nhọn.
- Giải thích bằng tỉ số lượng giác của các góc 30°, 45°,60°.
- Giải thích quan hệ giữa tỉ số lượng giác của hai góc phụ nhau.
- Biết dùng máy tính cầm tay để tính sin, côsin, tang, côtang của một góc nhọn.
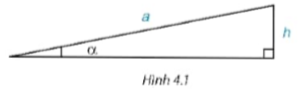
Ta có thể xác định “góc dốc" α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°).
1. KHÁI NIỆM TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Cho tam giác ABC vuông tại A. Xét góc nhọn B. Cạnh AC gọi là cạnh đối của góc B, cạnh AB gọi là cạnh kế của góc B (H.4.2).
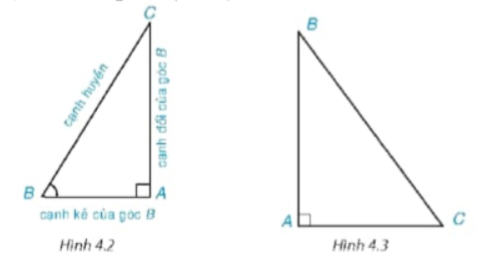
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kế của góc C.
Khái niệm sin, côsin, tang, côtang của góc nhọn α
HĐ1: Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A' có 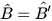 =α
=α
Chứng minh rằng:
a) △ABC  △A'B'C'
△A'B'C'
b) 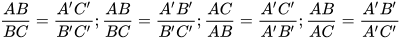
Nhận xét. Trong Hình 4.4, các tam giác vuông có cùng một góc nhọn α là đồng dạng với nhau. Vì vậy các tỉ số giữa cạnh đối và cạnh huyền (cạnh kề và cạnh huyền), cạnh đối và cạnh kề (cạnh kề và cạnh đối) của góc nhọn α là như nhau, cho dù độ dài các cạnh đối (các cạnh kề) của góc ở và các cạnh huyền có thể khác nhau với từng tam giác.
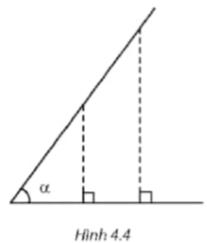
(Trang 68)
Cho góc nhọn α. Xét tam giác ABC vuông tại A có góc nhọn B bằng α. (H.4.5). Ta có:
– Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của α., kí hiệu sin α..
– Tỉ số giữa cạnh kế và cạnh huyền gọi là côsin của α., kí hiệu cos α..
– Tỉ số giữa cạnh đối và cạnh kế của góc α. gọi là tang của α., kí hiệu tan α..
– Tỉ số giữa cạnh kề và cạnh đối của góc α. gọi là côtang của α., kí hiệu cot α..
Chú ý. Ta có:
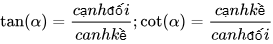
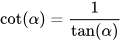
- Sin α, cos α, tan α, cot α gọi là các tỉ số lượng giác của góc nhọn α.
Sin, côsin của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất.
Ví dụ 1
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm (H.4.6).
Hãy tính các tỉ số lượng giác sin α, cos a, tan α với α = 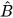
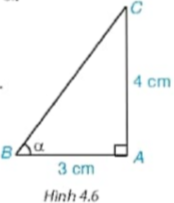
Giải
Xét △ABC vuông tại A, 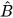 = α
= α
Theo Định lí Pythagore, ta có:
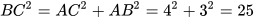 nên BC=5(cm)
nên BC=5(cm)
| sin α còn được viết là sin
|
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, ta có
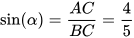 ,
, 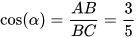 ,
, 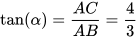 .
.
Luyện tập 1
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
(Trang 69)
Giá trị lượng giác sin, côsin, tang, côtang các các góc 30°, 45°, 60°
HĐ2 Cho tam giác ABC vuông cân tại A và AB=AC=a (H.4.7a)
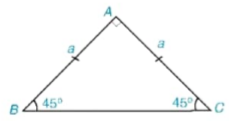
Hình 4.7a
a) Hãy tính BC và các tỉ số 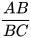 ,
, 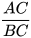 .
.
Từ đó suy ra sin 45°, cos 45°.
b) Hãy tính các tỉ số 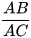 và
và 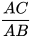 . Từ đó suy ra tan 45°, cot 45°.
. Từ đó suy ra tan 45°, cot 45°.
HĐ3 Xét tam giác đều ABC có cạnh bằng 2a.
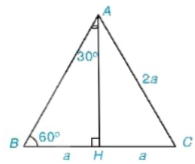
Hình 4.7b
a) Tính đường cao AH của tam giác ABC (H.4.7b).
b) Tính sin 30°, cos 30°, sin 60° và cos 60.
c) Tính tan 30°, cot 30°, tan 60° và cot60.
Từ HĐ2 và HĐ3, ta có bảng sau:
| α | 30° | 45° | 60° |
| sin α | 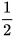 | 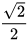 | 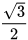 |
| cos α | 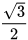 | 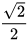 | 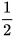 |
| tan α | 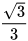 | 1 | 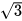 |
| cot α | 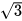 | 1 | 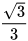 |
Ví dụ 2 Cho tam giác ABC vuông tại A có 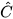 = 30° và BC = a (H.4.8). Tính các cạnh AB, AC theo a.
= 30° và BC = a (H.4.8). Tính các cạnh AB, AC theo a.
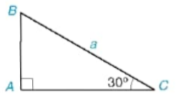
Hình 4.8
Giải
Ta có sin 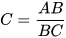 , suy ra AB = BC . sin C=a . sin30°
, suy ra AB = BC . sin C=a . sin30°
Theo bảng trên, sin30°=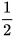 nên AB=
nên AB=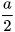 .
.
Tương tự, ta có cos 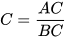 , suy ra AC=BC . cos C = a . cos30° =
, suy ra AC=BC . cos C = a . cos30° =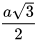 .
.
(Trang 70)
Luyện tập 2
Cho tam giác ABC vuông tại A có 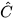 = 45° và AB = c. Tính BC và AC theo c.
= 45° và AB = c. Tính BC và AC theo c.
2 TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU
Tỉ số lượng giác của hai góc phụ nhau
HĐ4 Cho tam giác ABC vuông tại C, có 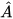 = a,
= a, 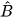 = β (H.4.9). Hãy viết các tỉ số lượng giác của góc α, β theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
= β (H.4.9). Hãy viết các tỉ số lượng giác của góc α, β theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
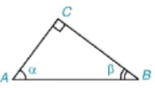
Hình 4.9
Định lí
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Chú ý. Cho α và β là hai góc phụ nhau (H.4.9), khi đó:
sinα = cosβ, cosα = sinβ, tanα = cotβ, cot α = tanβ.
| Về số đo, hai góc phụ nhau có thể coi là hai góc nhọn của một tam giác vuông.
|
Ví dụ 3
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45°:
sin 60°, cos 75°, sin 52°30', tan 80°, cot 82°.
Giải
Ta có:
sin 60° = cos (90° - 60°) = cos 30°;
cos 75° = sin (90° - 75°) = sin 15°;
sin 52°30′ = cos (90° - 52°30')= cos 37°30';
tan 80° = cot (90°-80°) = cot 10°;
cot 82° = tan (90°-82°) = tan 8°.
Luyện tập 3
Hãy giải thích tại sao sin 35° = cos 55°, tan 35° = cot55°.
(Trang 71)
3 SỬ DỤNG MÁY TÍNH CẦM TAY TÍNH TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
Ví dụ 4
Dùng MTCT, tính sin 27°, cos 32°15', tan 52°12' và cot35°23' (làm tròn đến chữ số thập phân thứ ba).
| Về số đo góc, dưới đơn vị độ (°) còn có các đơn vị phút (') và giây (") với 1° = 60', 1' = 60".
|
| Để tính | Bấm phím | Kết quả |
| sin 27° |  | 0,4539904997 |
| cos 32°15' |  | 0,8457278217 |
| tan 52°12' |  | 1,289192232 |
| cot 35°23' |  | 1,408003909 |
Làm tròn đến chữ số thập phân thứ ba ta được sin 27° ≈ 0,454, cos 32°15' ≈ 0,846, tan 52°12' ≈ 1,289; cot 35°23' ≈ 1,408.
Lưu ý: 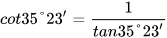
Nhận xét. Để tính cot 35°23', ta có thể tính trực tiếp như trên, hoặc có thể tìm góc phụ với góc 35°23' là 54°37' rồi dùng MTCT tính tan 54°37' và suy ra kết quả.
Luyện tập 4
Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:
a) sin 40°54'; b) cos 52°15';
c) tan 69°36'; d) cot 25°18'.
Chú ý. Sử dụng MTCT, ta còn có thể tìm được góc khi biết một trong các tỉ số lượng giác của góc đó.
Ví dụ 5
Dùng MTCT, tìm các góc (làm tròn đến phút) biết 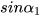 = 0,3214,
= 0,3214, 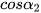 = 0,4321,
= 0,4321, 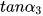 = 1,2742 và
= 1,2742 và 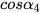 = 1,5384.
= 1,5384.
(Trang 72)
Giải
| Biết | Bấm phím | Kết quả | Bấm tiếp  |
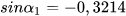 |  | 18,74761209 | 18°44' 51,4" |
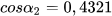 |  | 64,39909458 | 64°23' 56,74" |
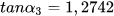 |  | 51,87495892 | 51°52' 29,85" |
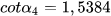 |  | 33,02491482 | 33°1' 29,69" |
Làm tròn đến phút ta được 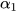 ≈ 18°45';
≈ 18°45'; 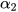 ≈ 64°24';
≈ 64°24'; 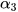 ≈ 51°52';
≈ 51°52'; 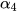 ≈ 33°1'.
≈ 33°1'.
Chú ý. Để tìm góc α khi biết cot α, ta có thể tìm góc (90° - α) (vì tan (90° – α) = cot α) rồi suy ra α.
Luyện tập 5 Dùng MTCT, tìm các góc α. (làm tròn đến phút), biết:
a) sin α = 0,3782; b) cos α= 0,6251; c) tan α = 2,154; d) cot a = 3,253.
Vận dụng
Trở lại bài toán ở tình huống mở đầu. Trong một toà chung cư, biết đoạn dốc vào sảnh toà nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Tranh luận
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được 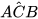 = α. và BC = a (H.4.10). Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết α = 55°, a = 70 m.
= α. và BC = a (H.4.10). Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết α = 55°, a = 70 m.
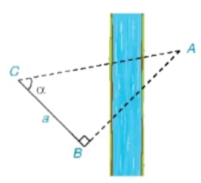
Hình 4.10
| Không thể tính được AB vì trong tam giác vuông ABC, theo định lí Pythagore, phải biết được hai cạnh mới tính được cạnh thứ ba.
| Với các dữ liệu đã biết là có thể tính được khoảng cách AB rồi.
|
Em hãy cho biết ý kiến của mình.
(Trang 73)
BÀI TẬP
4.1. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết:
a) AB= 8 cm, BC = 17 cm; b) AC = 0,9 cm, AB = 1,2 cm.
4.2. Cho tam giác vuông có một góc nhọn 60° và cạnh kề với góc 60° bằng 3 cm. Hãy tính cạnh đối của góc này.
4.3. Cho tam giác vuông có một góc nhọn bằng 30° và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.
4.4. Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và 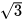 . Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).
. Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).
4.5. a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
sin 55°, cos 62°, tan 57°, cot 64°.
b) Tính 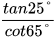 , tan 34°-cot 56°.
, tan 34°-cot 56°.
4.6. Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba):
a) sin 40°12'; b) cos 52°54';
c) tan 63°36'; d) cot 25°18'.
4.7. Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sin x = 0,2368; b) cos x = 0,6224;
c) tan x = 1,236; d) cot x = 2,154.
EM CÓ BIẾT? (Đọc thêm)
LỊCH SỬ RA ĐỜI CÁC TỪ sin, côsin, tang, côtang
Ở thế kỉ II, nhà thiên văn người Hy Lạp Ptolemy (85 – 165) đã nghiên cứu mối liên hệ giữa độ dài cung tròn và dây căng cung tròn đó. Sau đó, những nhà thiên văn người Hindu đã nghiên cứu mối liên hệ giữa bán cung và nửa dây, gọi dây căng cung là jiva. Nhà thiên văn người Ả Rập Al-Battani (850 – 929) đã phiên âm jiva thành djiba mà nghĩa đen là “nếp gấp". Đến năm 1150, nhà phiên dịch người Ý Gerard de Cremone (1114 – 1187) dịch djiba sang tiếng Latinh thành sinus viết tắt là sin (trên hình: (O) là đường tròn bán kính bằng 1, P là điểm chính giữa của cung nhỏ MN, H là trung điểm của dây MN, khi đó sin 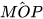 = HM).
= HM).
Năm 1583, nhà vật lí và toán học người Đức Thomas Finck đã đưa vào từ "tang" (trong từ ngữ khoa học Ả Rập, chữ tang có nghĩa là bóng của một vật) và các kí hiệu sin.com, tan.com (chữ com là viết tắt của chữ complemantary, ý nói góc phụ). Mãi 40 năm sau, người ta mới dùng kí hiệu côsin, côtang thay cho sin.com, tan.com.
(theo Stella Baruk, Dictionnaire de mathématiques élémentaires, Seuil, Pháp, 1992)
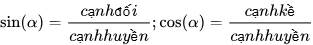
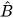 hay sin B. Tương tự cho cos α, tan α và cot α.
hay sin B. Tương tự cho cos α, tan α và cot α.







































