(Trang 38)
Khái niệm, thuật ngữ
- Bất phương trình bậc nhất một ẩn
- Nghiệm của bất phương trình
Kiến thức, kĩ năng
- Khái niệm bất phương trình bậc nhất một ẩn.
- Khái niệm nghiệm của bất phương trình bậc nhất một ẩn.
- Giải bất phương trình bậc nhất một ẩn.
Bạn Thanh có 100 nghìn đồng. Bạn muốn mua một cái bút giá 18 nghìn đồng và một số quyển vở, mỗi quyển vở giá 7 nghìn đồng. Hỏi bạn Thanh mua được nhiều nhất bao nhiêu quyển vở?
1. KHÁI NIỆM BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Khái niệm bất phương trình bậc nhất một ẩn
Trong bài toán mở đầu, nếu kí hiệu số vỏ mà Thanh mua là x (x ∈ N*) thì x phải thoả mãn hệ thức 7x + 18 ≤ 100. Khi đó ta nói hệ thức 7x+18 ≤ 100 là bất phương trình với ẩn là x.
Trong bất phương trình này, ta gọi 7x + 18 là vế trái, 100 là vế phải.
Ta có thể biến đổi bất phương trình này về dạng 7x – 82 ≤ 0.
Hệ thức này là bất phương trình bậc nhất với ẩn là x.
Bất phương trình dạng ax+b<0 (hoặc ax+b>0; ax+b≤0; ax+b ≥ 0 ) trong đó a, b là hai số đã cho, a ≠ 0 được gọi là bất phương trình bậc nhất một ẩn x.
Ví dụ 1: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn x?
a) 3x+16 ≤ 0; b) -5x+5>0;
c) x2-4>0; d) - 3x < 0.
Giải:
a), b), d) là bất phương trình bật nhất một ẩn x.
c) không là bất phương trình bật nhất một ẩn x vì x² - 4 là một đa thức bật hai.
(Trang 39)
Luyện tập 1: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn x?
a) -3x+7≤0; b) 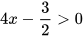 ; c)
; c) 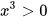
Nghiệm của bất phương trình
- Xét bất phương trình 3x +8 <20.
Khi thay giá trị x=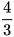 vào bất phương trình, ta được
vào bất phương trình, ta được  là một khẳng định đúng.
là một khẳng định đúng.
Ta nói số 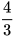 (hay giá trị x=
(hay giá trị x=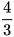 ) là một nghiệm của bất phương trình.
) là một nghiệm của bất phương trình.
Khi thay giá trị x = 5 vào bất phương trình, ta được 3.5+8< 20 là một khẳng định sai.
Ta nói số 5 (hay giá trị x =5) không phải là nghiệm của bất phương trình.
- Số
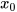 là một nghiệm của bất phương trình A(x) < B(x) nếu A(
là một nghiệm của bất phương trình A(x) < B(x) nếu A(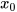 )<B(
)<B(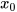 ) là khẳng định đúng.
) là khẳng định đúng. - Giải một bất phương trình là tìm tất cả các nghiệm của bất phương trình đó.
Luyện tập 2
Trong các số –2; 0; 5, những số nào là nghiệm của bất phương trình 2x – 10 < 0?
2. CÁCH GIẢI BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Cách giải bất phương trình bậc nhất một ẩn
HĐ. Xét bất phương trình 5x + 3 < 0. (1)
Hãy thực hiện các yêu cầu sau để giải bất phương trình (1):
a) Sử dụng tính chất của bất đẳng thức, cộng vào hai về của bất phương trình (1) với –3, ta được một bất phương trình, kí hiệu là (2).
b) Sử dụng tính chất của bất đẳng thức, nhân vào hai vế của bất phương trình (2) với 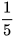 (tức là chia cả hai về của bất phương trình (2) cho hệ số của x là 5) để tìm nghiệm của bất phương trình.
(tức là chia cả hai về của bất phương trình (2) cho hệ số của x là 5) để tìm nghiệm của bất phương trình.
Bất phương trình bậc nhất một ẩn ax + b < 0 (a ≠ 0) được giải như sau:
ax + b < 0
ax < -b
- Nếu a > 0 thì
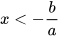 .
. - Nếu a < 0 thì x:
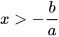
Chú ý. Các bất phương trình ax + b > 0, ax + b ≤ 0, ax + b ≥ 0 được giải tương tự.
(Trang 40)
Ví dụ 2: Giải bất phương trình -2x-4>0.
Giải. Ta có -2x-4>0
-2x>0+4 <- Cộng hai vế của bất phương trình với 4.
-2x>4
x<4.(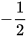 ) <- nhân hai vế với số âm
) <- nhân hai vế với số âm 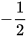 và đổi chiền bất đẳng thức.
và đổi chiền bất đẳng thức.
x<-2
Vậy nghiệm của bất phương trình là x<-2.
Luyện tập 3: Giải các bất phương trình:
a) 6x+5<0; b) -2x-7>0.
Ví dụ 3: Giải bài toán ở tình huống mở đầu.
Giải
Gọi x (quyển) là số vở mà Thanh có thể mua. Theo bài ra, ta có bất phương trình:
7x+18≤100
7x≤100-18
7x≤82
x≤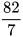
Vì số vở là số tự nhiên nên Thanh có thể mua nhiều nhất 11 quyển vở.
Chú ý: Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng ax+b<0, ax+b>0, ax+b≤0, ax+b≥0.
Ví dụ 4: Giải các bất phương trình:
a) 2x+5<3x-4; b) -3x+5≥-4x+3.
Giải
a) Ta có 2x+5<3x-4
2x-3x<-4-5
-x<-9
x>9.
Vậy nghiệm của bất phương trình là x>9.
b) Ta có -3x+5≥-4x+3
-3x+4x≥3-5
x≥-2
Vậy nghiệm của bất phương trình là x≥-2.
(Trang 41)
Ví dụ 5: Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 12 tháng là 7,4%/năm. Bà Mai dự kiến gửi một khoản tiền vào ngân hàng này và cần số tiền lãi hàng năm ít nhất là 60 triệu để chi tiêu. Hỏi số tiền bà Mai cần gửi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng)?
Giải. Gọi x (triệu đồng) là số tiền bà Mai cần gửi tiết kiệm. Ta có số tiền lãi gửi tiết kiệm x (triệu đồng) trong một năm là 0,074 . x (triệu đồng).
Để có số tiền lãi ít nhất là 60 triệu đồng/năm thì ta phải có:
0,074≥60
x≥60:0,074
x ≥ 810,81.
Vậy bà Mai cần gửi ngân hàng ít nhất 811 triệu đồng.
Luyện tập 4: Giải các bất phương trình sau:
a) 5x+7>8x-5; b) -4x+3≤ 3x-1.
Vận dụng. Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 25 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó chỉ có một đáp án đúng. Người ứng tuyển chọn đáp án đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ đi 1 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 5 điểm và theo quy định người ứng tuyển phải trả lời hết 25 câu hỏi; người nào có số điểm từ 25 trở lên mới được dự thi vòng tiếp theo. Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được vào vòng tiếp theo?
BÀI TẬP
2.16. Giải các bất phương trình sau:
a) x-5≥0; b) x + 5 ≤ 0; c) -2x-6> 0; d) 4x-12 < 0;
2.17. Giải các bất phương trình sau:
a) 3x + 2 > 2x + 3; b) 5x + 4 < -3x-2.
2.18. Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0,4%. Hỏi nếu muốn có số tiền lãi hằng tháng ít nhất là 3 triệu đồng thì số tiền gửi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng)?
2.19. Một hãng taxi có giá mở cửa là 15 nghìn đồng và giá 12 nghìn đồng cho mỗi kilômét tiếp theo. Hỏi với 200 nghìn đồng thì hành khách có thể di chuyển được tối đa bao nhiêu kilômét (làm tròn đến hàng đơn vị)?
2.20. Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình 6,7 kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác lái xe nặng 65 kg?
(Trang 42)
BÀI TẬP CUỐI CHƯƠNG II
A. TRẮC NGHIỆM
2.21. Nghiệm của bất phương trình -2x+1<0 là
A. 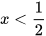 B.
B.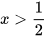 C.
C. 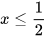 D.
D. 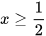
2.22. Điều kiện xác định của phương trình 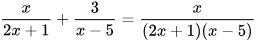 là
là
A. 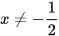 B.
B. 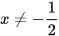 và x≠-5 C. x≠5 ; B.
và x≠-5 C. x≠5 ; B. 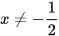 và x≠5
và x≠5
2.23. Phương trình x-1=m+4 có nghiệm lớn hơn 1 với
A. m≥-4. B. m≤4. C. m>-4. D. m<-4.
2.24. Nghiệm của bất phương trình 1-2x≥2-x là
A. x>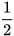 . B. x<
. B. x<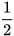 . C. x≤-1. D. x≥-1.
. C. x≤-1. D. x≥-1.
2.25. Cho a>b. Khi đó ta có:
A. 2a>3b b. 2a>2b+1 C. 5a+1>5b+1 D. -3a<-3b-3
TỰ LUẬN
2.26. Giải các phương trình sau:
a) 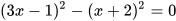 b)
b) 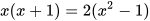
2.27. Giải các phương trình sau:
a)  ; b)
; b) 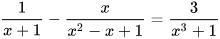
2.28. Cho a<b, hãy so sánh:
a) a+b+5 với 2b+5; b) -2a-3 với -(a+b)-3.
2.29. Giải các phương trình sau:
a) 2x+3(x+1)>5x-(2x-4); b) (x+1)(2x-1)<2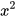 -4x+1.
-4x+1.
2.30. Một hãng viễn thông nướ cngoaif có hai gói cưới như sau:
| Gói cước A | Gói cưới B |
| Cước thuê bao hàng tháng là 32 USD 45 phút miễn phí 0,4 USD cho mỗi phút thêm | Cước thuê bao hàng tháng là 44 USD Không có phút miễn phí 0,25 USD/phút |
(Trang 43)
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó.
b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?
2.31. Thanh tham dự một kì kiểm tra năng lực tiếng Anh gồm 4 bài kiểm tra nghe, nói,
đọc và viết. Mỗi bài kiểm tra có điểm là số nguyên từ 0 đến 10. Điểm trung bình của ba bài kiểm tra nghe, nói, đọc của Thanh là 6,7. Hỏi bài kiểm tra viết của Thanh cần được bao nhiêu điểm để điểm trung bình cả 4 bài kiểm tra được từ 7,0 trở lên? Biết điểm trung bình được tính gần đúng đến chữ số thập phần thứ nhất.
2.32. Để lập đội tuyển năng khiếu về bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển. Hỏi một học sinh muốn được chọn vào đội tuyển thì phải ném ít nhất bao nhiêu quả vào rổ?
EM CÓ BIẾT? (Đọc thêm)
BẤT ĐẲNG THỨC GIỮA TRUNG BÌNH CỘNG VÀ TRUNG BÌNH NHÂN
Cho hai số a, b ≥0. Trung bình cộng của hai số là 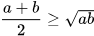 (1)
(1)
Bất đẳng thức (1) được gọi là bất đẳng thức giữa trung bình cộng và trung bình nhân cho hai số không âm a và b (thường viết tắt là AB-GM). Ta cũng thường gọi bất đẳng thức trên là bất đẳng thức Cauchy.

Cauchy (1789-1857) là một nhà toán học Pháp. Ông là giáo sư của Đại học Bách khoa Paris và Viện sĩ Viện hàn lâm khoa học Pháp. Ông có nhiều công trình nghiên cứu toán học có giá trị liên quan đến nhiều lĩnh vực nghiên cứu khác nhau trong giải thích, Đại số, Số học, Hệ động lực,...
(Theo: Benis-Sinaceur, Hourya(1973), Cauchy et Bolzano, Revued Histoire des Sciences.26(2):97-112)


































