(Trang 44)
Chương III. CĂN BẬC HAI VÀ CĂN BẬC BA
Ở lớp 7, các em đã làm quen với khái niệm căn bậc hai số học; biết cách tìm căn bậc hai số học của một số thực không âm và biết cách so sánh các căn bậc hai số học của hai số không âm. Trong chương này, chúng ta sẽ mở rộng khái niệm căn bậc hai số học.
Bài 7: CĂN BẬC HAI VÀ CĂN THỨC BẬC HAI
Khái niệm, thuật ngữ
- Căn bậc hai
- Căn thức bậc hai
- Điều kiện xác định của căn thức bậc hai
Kiến thức, kĩ năng
- Nhận biết căn thức bậc hai của một số thực không âm. Tính được giá trị đúng (hoặc gần đúng) căn bậc hai của một số thực dương bằng máy tính cầm tay.
- Nhận biết căn thức bậc hai của một biết thức đại số, điều kiện xác định của căn thức bậc hai; tính được giá trị căn thức bậc hai tại những giá trị đã cho của biến.
- Sử dụng hằng đẳng thức căn bậc hai của một bình phương để đơn giản căn thức bậc hai.
- Trong Vật lí, quãng đường S (tính bằng mét) của một vật rơi tự do được cho bởi công thức S = 4,9t², trong đó t là thời gian rơi (tính bằng giây). Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?
(Trang 45)
1. CĂN BẬC HAI
Tìm hiểu khái niệm căn bậc hai
HĐ1. Tìm các số thực x sao cho x² = 49
Căn bậc hai của số thực không âm a là số thực x sao cho x² = a.
Nhận xét
- Số âm không có căn bậc hai;
- Số 0 có một căn bậc hai duy nhất là 0;
- Số dương a có đúng hai căn bậc hai đối nhau là 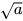 (căn bậc hai số học của a) và -
(căn bậc hai số học của a) và -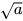 .
.
Ví dụ 1: Tìm căn bậc hai của 81.
Giải
Ta có 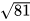 = 9 nên 81 có hai căn bậc hai là 9 và – 9.
= 9 nên 81 có hai căn bậc hai là 9 và – 9.
Luyện tập 1: Tìm căn bậc hai của 121.
Tính căn bậc hai của một số bằng máy tính cầm tay
Để tính các căn bậc hai của một số a > 0, chỉ cần tính 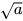 . Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
. Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Ví dụ 2
Sử dụng MTCT, tỉnh căn bậc hai của 11,1 (làm tròn đến chữ số thập phân thứ hai).
Giải
Bấm các phím  màn hình hiện kết quả là 3,33166625. Làm tròn kết quả đến chữ số thập phân thứ hai ta được
màn hình hiện kết quả là 3,33166625. Làm tròn kết quả đến chữ số thập phân thứ hai ta được 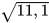 ≈ 3,33.
≈ 3,33.
Vậy căn bậc hai của 11,1 (làm tròn đến chữ số thập phân thứ hai) là 3,33 và –3,33.
Luyện tập 2. Sử dụng MTCT tìm căn bậc hai của (làm tròn đến chữ số thập phân thứ hai).
Tính chất của căn bậc hai
HĐ2 Tinh và so sánh 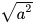 và
và 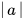 trong mỗi trường hợp sau:
trong mỗi trường hợp sau:
a) a = 3; b) a = -3.
(Trang 46)
Tính chất:
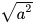 =
=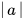 với mọi số thực a.
với mọi số thực a.
Ví dụ 3: Không sử dụng MTCT, tính:
a) 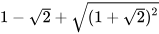 ; b)
; b) 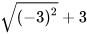 .
.
Giải
a) Ta có 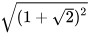 =
=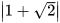 = 1+
= 1+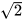 nên 1-
nên 1-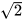 +
+ 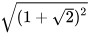 =1-
=1-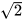 +(1+
+(1+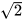 )=2
)=2
b) Ta có 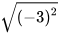 =
=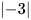 =3 nên
=3 nên 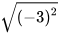 +3=3+3=6
+3=3+3=6
Luyện tập 3
a) Không sử dụng MTCT, tính: 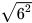 ;
;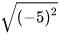 ;
;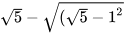
b) So sánh 3 với 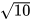 bằng hai cách:
bằng hai cách:
- Sử dụng MTCT
- Sử dụng tính chất của căn bậc hai số học ở lớp 7: Nếu 0≤a<a thì 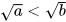
2. CĂN THỨC BẬC HAI
Căn thức bậc hai
HĐ3. Viết biểu thức tính độ dài cạnh huyền BC của tam giác vuông ABC, biết AB = 3 cm và AC = x cm.
Biểu thức nhận được trong HĐ3 có dạng √A, trong đó A là một biểu thức đại số. Tổng quát, ta có định nghĩa:
Căn thức bậc hai là biểu thức có dạng √A, trong đó A là một biểu thức đại số. A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.
HĐ4. Cho biểu thức C = 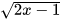 .
.
a) Tính giá trị của biểu thức tại x = 5.
b) Tại x = 0 có tính được giá trị của biểu thức không? Vì sao?
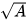 xác định khi A lấy giá trị không âm và ta thường viết là A ≥ 0. Ta nói A≥ 0 là điều kiện xác định (hay điều kiện có nghĩa) của
xác định khi A lấy giá trị không âm và ta thường viết là A ≥ 0. Ta nói A≥ 0 là điều kiện xác định (hay điều kiện có nghĩa) của 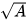 .
.
(Trang 47)
Ví dụ 4: Xét căn thức 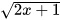
a) Tìm điều kiện xác định của căn thức.
b) Tính giá trị của căn thức đã cho tại x = 0 và x = 4.
Giải
a) Điều kiện xác định của căn thức là 2x+1≥ 0 hay x ≥ 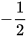
b) Tại x = 0 (thỏa mãn điều kiện xác định) căn thức có giá trị là 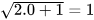
Tại x = 4 (thoả mãn điều kiện xác định) căn thức có giá trị là 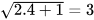
Luyện tập 4. Cho căn thức 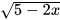
- a) Tìm điều kiện xác định của căn thức.
- b) Tính giá trị của căn thức tại x = 2.
Hằng đẳng thức 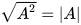
Tương tự như căn bậc hai của một số thực không âm, với A là một biểu thức, ta cũng có:
- Với A≥0 ta có
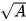 ≥0;
≥0; 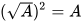
Ví dụ 5: Rút gọn các biểu thức sau:
a)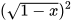 với x<0
với x<0
b) 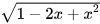 với x>2
với x>2
Giải
a) Từ giả thiết x<0 suy ra 1-x>0. Do đó
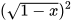 =1-x. <- hằng đẳng thức
=1-x. <- hằng đẳng thức 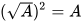 với mọi A≥0
với mọi A≥0
b) Áp dụng hằng đẳng thức bình phương của một hiệu và bằng đẳng thức 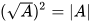
ta có 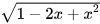 =
=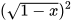 =
=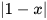
Do giả thiết x>2 suy ra 1-x<2 nên 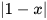 =-(1-x)=x-1. Vì vậy
=-(1-x)=x-1. Vì vậy
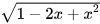 =
=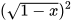 =x-1 với x>2
=x-1 với x>2
(Trang 48)
Luyện tập 5:
a) Rút gọn biểu thức 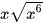 (x<0)
(x<0)
b) Rít gọn và tính giá trị của biểu thức 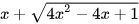 tại x=-2,5
tại x=-2,5
Vận dụng: Trở lại tình huống mở đầu.
a) Viết công thức tính thời gian t (giây) cần thiết để vật rơi được quãng đường S (mét).
b) Sử dụng công thức tìm được trong câu a, hãy trả lời câu hỏi trong tình huống mở đầu.
BÀI TẬP
3.1. Tìm căn bậc hai của mỗi số sau (làm tròn đến chữ số thập phân thứ hai):
a) 24,5; b) 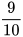
3.2. Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng 2m². Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét?
3.3. Tìm điều kiện xác định của 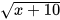 và tính giá trị của căn thức tại x=-1.
và tính giá trị của căn thức tại x=-1.
3.4. Tính:
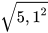 ;
; 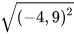 ;
; 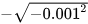
3.5. Rút gọn các biểu thức sau:
a) 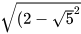 ;
;
b) 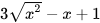 (x<0);
(x<0);
c)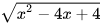 (x<2).
(x<2).
3.6. Không dùng MTCT, chứng tỏ biểu thức A có giá trị là số nguyên:
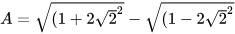 .
.



































