(Trang 83)
Chương V. ĐƯỜNG TRÒN
HÌNH HỌC PHẲNG
Trong đời sống thực tế, chúng ta thấy có rất nhiều hình ảnh của đường tròn hay hình tròn như bánh xe, vành nón, mặt trống, biển báo giao thông, ... Vậy đường tròn là gì? Đường tròn có những tính chất gì? Chương này sẽ giúp các em khám phá những điều lí thú về đường tròn.
Bài 13: MỞ ĐẦU VỀ ĐƯỜNG TRÒN
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
|
|
Bạn Oanh có một mảnh giấy hình tròn nhưng không còn dấu vết của tâm. Theo em, Oanh làm thế nào để tìm lại được tâm của hình tròn đó.
1 ĐƯỜNG TRÒN
Đường tròn, điểm thuộc đường tròn
Ở lớp dưới các em đã biết cách dùng compa để vẽ đường tròn. Vậy đường tròn là gì? Ta định nghĩa:
Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O, R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
(Trang 84)
• Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).
• Nếu A là một điểm của đường tròn (O) thì ta viết A ∈ (O). Khi đó, ta còn nói đường tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).
Nhận xét
1) Trên Hình 5.1, ta thấy điểm A nằm trên, điểm C nằm trong và điểm B nằm ngoài đường tròn (O). Một cách tổng quát, ta có:
– Điểm M nằm trên đường tròn (O; R) nếu OM = R;
– Điểm M nằm trong đường tròn (O; R) nếu OM < R;
– Điểm M nằm ngoài đường tròn (O; R) nếu OM > R.
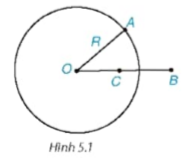
Hình 5.1
2) Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R).
Ví dụ 1
Gọi O là trung điểm của đoạn thẳng AB. Chứng minh rằng đường tròn (O; OA) đi qua B.
Giải (H.5.2)
Vì O là trung điểm của đoạn AB nên OB = OA. Do đó B ∈ (O, OA), nói cách khác, đường tròn (O, OA) đi qua B.
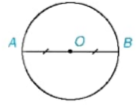
Hình 5,2
Chú ý. Ở lớp dưới, ta đã biết đoạn AB trong Ví dụ 1 là một đường kính của đường tròn (O). Do đó (C) còn gọi là đường tròn đường kính AB.
Luyện tập 1
Cho tam giác ABC vuông tại A. Chứng minh rằng điểm A thuộc đường tròn đường kính BC.
Vận dụng 1
Trong mặt phẳng toạ độ Oxy, cho các điểm A(3; 0), B(-2; 0), C(0; 4). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O; 3)?
(Trang 85)
2 TÍNH ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
Đối xứng tâm và đối xứng trục
1) Đối xứng tâm (H.5.3)
Hai điểm M và M' gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM'.
Chẳng hạn, nếu O là giao điểm hai đường chéo của hình bình hành ABCD thì OA = OC nên A và C đối xứng với nhau qua O. Tương tự, B và D đối xứng với nhau qua O.
Hình 5.3
2) Đối xứng trục (H.5.4)
Hai điểm M và M' gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn thẳng MM'.
Chẳng hạn, nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.
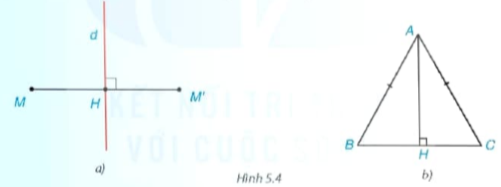
Tâm và trục đối xứng của đường tròn
HĐ Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tuỳ ý đi qua O cũng thuộc (O).
Khi đó ta nói O là tâm đối xứng của đường tròn (O); d là trục đối xứng của đường tròn (O), ta có:
• Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó.
• Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó.
| Đường tròn có một tâm đối xứng, nhưng có vô số trục đối xứng.
|
(Trang 86)
Ví dụ 2
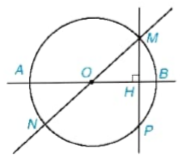
Cho điểm M nằm trên đường tròn (O) đường kính AB. Sử dụng tính đối xứng của (O), hãy nêu cách tìm:
a) Điểm N đối xứng với điểm M qua tâm O;
b) Điểm P đối xứng với điểm M qua đường thẳng AB.
Hình 55
Giải (H.5.5)
a) Do O là tâm đối xứng của (O) nên điểm N đối xứng với điểm M qua tâm O phải vừa thuộc (O), vừa thuộc OM. Vậy N là giao điểm của (O) với đường thẳng OM.
b) Do AB là trục đối xứng của (O) nên điểm P đối xứng với điểm M qua AB phải vừa thuộc (O), vừa thuộc đường vuông góc hạ từ M xuống AB. Vậy P là giao điểm của (O) với đường thẳng đi qua M và vuông góc với AB.
Luyện tập 2
Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).
Vận dụng 2
Trở lại tình huống mở đầu, bằng cách gấp đôi mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm lại được tâm của hình tròn. Em hãy làm thử xem.
BÀI TẬP
5.1. Trong mặt phẳng toạ độ Oxy, cho các điểm M(0; 2), N(0; –3) và P(2; −1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O,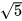 
)? Vì sao?
5.2. Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
5.3. Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
5.4. Cho hình vuông ABCD có E là giao điểm của hai đường chéo.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó.
b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3 cm.
