Trang 100
Ví dụ 1
Gọi tên đỉnh, cạnh, mặt bên, mặt đáy của hình lăng trụ đứng tam giác ở Hình 10.37.
Giải
Các đỉnh của hình lăng trụ là: A, B, C, M, N, P.
Các cạnh của hình lăng trụ là: AB, BC, CA, MN, NP, PM, AM, BN, CP.
Các mặt bên của hình lăng trụ là các hình chữ nhật ABNM, BCPN, ACPM.
Các mặt đáy của hình lăng trụ là các tam giác ABC và MNP.
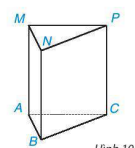
Hình 10.37
Ví dụ 2
Ông Khôi làm một khối gỗ hình lăng trụ đứng tam giác, kích thước như Hình 10.38, để chèn bánh xe. Tính thể tích của khối gỗ.
Giải
Thể tích của khối gỗ là:
V = Sđáy . h =  . 60 . 90 . 70 = 189 000 (cm3) = 0,189 (m3)
. 60 . 90 . 70 = 189 000 (cm3) = 0,189 (m3)
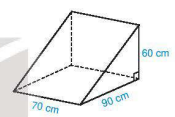
Hình 10.38
Ví dụ 3
Chi đội của bạn Trang dựng một lều ở lăng trụ đứng tam giác với kích thước như Hình 10.39.

Hình 10.39
a) Tính thể tích khoảng không bên trong lều.
b) Biết lều phủ vải bạt 4 phía, trừ mặt tiếp đất. Tính diện tích vải bạt cần phải có để dựng lều.
Giải
a) Diện tích đáy lăng trụ là: Sđáy = (3,2 . 1,2) : 2 = 1,92 (m²).
Thể tích khoảng không bên trong lều là: V = Sđáy . h = 1,92 - 5 = 9,6 (m³).
b) Diện tích vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5 m và 3,2 m.
Diện tích xung quanh lăng trụ là: Sxq = C . h = (2+2+3,2) . 5 = 36 (m²).
Diện tích toàn phần của hình lăng trụ là: Stp = Sxq + 2Sđáy = 36 + 2 . 1,92 = 39,84 (m²).
Diện tích mặt bên kích thước 5 m và 3,2 m là: 5 . 3,2 = 16 (m²).
Vậy diện tích vải bạt cần có để dựng lều là: 39,84 - 16 = 23,84 (m²).
Trang 101
BÀI TẬP
10.17. Viết tên đỉnh, cạnh, mặt bên, mặt đáy của hình lăng trụ đứng tứ giác ở Hình 10.40.
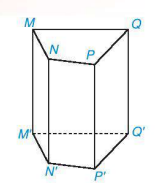
Hình 10.40
10.18. Một cái bánh ngọt có dạng hình lăng trụ đứng tam giác, kích thước như Hình 10.41.
a) Tính thể tích cái bánh.
b) Nếu phải làm một chiếc hộp để đựng vừa khít cái bánh này thì diện tích vật liệu cần dùng là bao nhiêu (coi mép dán không đáng kể)?
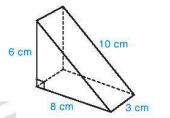
Hình 10.41
10.19. Người ta đào một đoạn mương có dạng hình lăng trụ đứng tứ giác như Hình 10.42. Biết mương có chiều dài 20 m, sâu 1,5 m, bề mặt có chiều rộng 1,8 m và đáy mương rộng 1,2 m. Tính thể tích đất phải đào lên.

Hình 10.42



































