Trang 72
| Khái niệm, thuật ngữ
| Kiến thức, kĩ năng
|
Hình 9.26 mô phỏng một miếng bìa hình tam giác ABC đặt thăng bằng trên giá nhọn tại điểm G. Điểm đó được B xác định như thế nào và có gì đặc biệt?
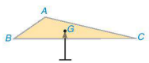
Hình 9.26
1. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN TRONG MỘT TAM GIÁC
Đường trung tuyến của tam giác
Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC (H.9.27).
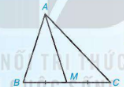
Hình 9.27
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của tam giác ABC.
? Mỗi tam giác có mấy đường trung tuyến?
Sự đồng quy của ba đường trung tuyến
HĐ1. Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện (tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp (ba đường trung tuyến) có cùng đi qua một điểm không (H.9.28).

Hình 9.28
Trang 73
HĐ2 Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A, B, C rồi vẽ tam giác ABC (H.9.29).
Vẽ hai đường trung tuyến BN, CP, chúng cắt nhau tại G; tia AG cắt cạnh BC tại M.
• AM có phải là đường trung tuyến của tam giác ABC không?
• Hãy xác định các tỉ số 
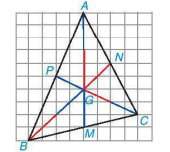
Hình 9.29
Người ta chứng minh được định lí sau:
Định lí 1
Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mỗi đỉnh một khoảng bằng  độ dài đường trung tuyến đi qua đỉnh ấy.
độ dài đường trung tuyến đi qua đỉnh ấy.
Chẳng hạn, trong tam giác ABC (H.9.30), các đường trung tuyến AM, BN, CP đồng quy tại điểm G và ta có

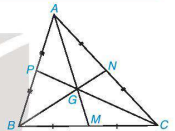
Hình 9.30
Chú ý. Điểm đồng quy của ba đường trung tuyến gọi là trọng tâm tam giác.
Ví dụ 1
Cho tam giác ABC với AM là trung tuyến và G là trọng tâm tam giác.
a) Chứng minh GA = 2GM.
b) Biết GM = 12 cm, tính GA.
Giải (H.9.31)
a)
| GT | △ABC có trung tuyến AM, trọng tâm G. |
| KL | GA = 2GM. |
Chứng minh
Vì G là trọng tâm tam giác ABC nên  hay
hay  . Ta có GM = MA - GA = MA -
. Ta có GM = MA - GA = MA -  =
= 
Vậy GA =  = 2 . (
= 2 . ( ) = 2GM.
) = 2GM.

Hình 9.31
b) Khi GM = 2 cm thì GA = 4 cm.
Luyện tập 1
Trong tam giác ABC ở Ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.
Trang 74
Tranh luận

Tớ tìm trọng tâm của một tam giác bằng cách lấy giao điểm của hai đường trung tuyến.
Tớ còn cách khác nữa cơ.
Các em có những cách nào?
Vận dụng 1
Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không.
2. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC
Đường phân giác của tam giác
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì đoạn thẳng AD được gọi là đường phân giác (xuất phất tức đỉnh A) của tam giác ABC (H.9.32).
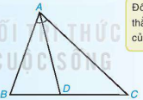
Hình 9.32

Đôi khi ta cũng gọi đường thẳng AD là đường phân giác của tam giác ABC.
Mỗi tam giác có mấy đường phân giác?
Sự đồng quy của ba đường phân giác
HĐ3 Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33).
Hình 9.33
Trang 75
Ta có thể chứng minh được định lí sau:
Định lí 2
Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Chẳng hạn, trong tam giác ABC (H.9.34), các đường phân giác AD, BE, CF đồng quy tại I và IH = IK = IL.
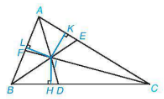
Hình 9.34
Ví dụ 2
Chứng minh rằng trong tam giác ABC cân tại A, giao điểm của ba đường phân giác nằm trên đường trung tuyến xuất phát từ đỉnh A (H.9.35).
Giải
| GT | △ABC, AB = AC, I là giao điểm của ba đường phân giác. |
| KL | AI là đường trung tuyến của △ABC. |
Chứng minh
Gọi M là giao điểm của đường thẳng AI và BC.
Hai tam giác ABM và ACM có:
KẾT NỐI TRI THỨC
AB = AC(gt),
AM chung,
 =
=  (do AI là đường phân giác của góc BAC).
(do AI là đường phân giác của góc BAC).
Do đó △ABM =△ACM (c.g.c).
Suy ra BM = CM hay M là trung điểm của BC.
Vậy AI là đường trung tuyến của tam giác ABC.
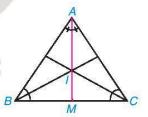
Hình 9.35
Luyện tập 2
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm 1. Hỏi Cl có là đường phân giác của góc C không?
Vận dụng 2
Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.
Trang 76
BÀI TẬP
9.20. Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu "?" để được các đẳng thức:
BG = ? BN, CG = ? CP;
BG = ? GN, CG = ? GP.
9.21. Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
9.22. Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
9.23. Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120°.
9.24. Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
9.25. Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.
a) Hãy giải thích tại sao DP = DR.
b) Hãy giải thích tại sao DP = DQ.
c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A?
(Đây là một cách chứng minh Định lí 2)

Mọi điểm trên tia phân giác của một góc cách đều hai cạnh của góc đó. Ngược lại, mọi điểm nằm bên trong góc, cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.



































