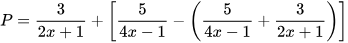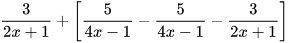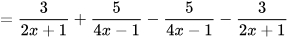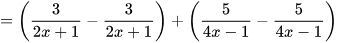(Trang 15)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Phép cộng và phép trừ các phân thức đại số | - Thực hiện phép cộng và phép trừ phân thức đại số. - Vận dụng các tính chất giao hoán, kết hợp của phép cộng phân thức và quy tắc dấu ngoặc với phân thức trong tính toán. |
| Hãy rút gọn biểu thức:
| Không cần tính toán, em thấy ngay kết quả P=0 | Làm thế nào mà Vuông thấy ngay được kết quả thế nhỉ? |
 |  |  |
1 CỘNG HAI PHÂN THỨC CÙNG MẪU
Quy tắc cộng hai phân thức cùng mẫu
Ở lớp 6, các em đã biết để cộng các phân số cùng mẫu ta chỉ cần cộng các tử số và giữ nguyên mẫu số. Phép cộng các phân thức cùng mẫu cũng tương tự như vậy.
Hãy thực hiện các yêu cầu sau để làm phép cộng 
HĐ1 Cộng các tử thức của hai phân thức đã cho.
HĐ2 Viết phân thức có tử là tổng các tử thức và mẫu là mẫu thức chung ta được kết quả của phép cộng đã cho.
Tổng quát, ta có quy tắc sau:
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức: 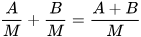 . . |
Chú ý. Kết quả của phép cộng hai phân thức được gọi là tổng của hai phân thức đó. Ta thường viết tổng dưới dạng rút gọn.
Ví dụ 1
Cộng hai phân thức 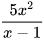 và
và 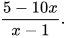
Giải
Ta có:
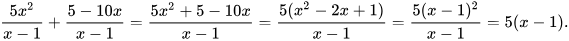
(Trang 16)
Luyện tập 1 Tính các tổng sau:
a) 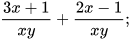 b)
b) 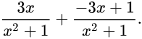
2 CỘNG HAI PHÂN THỨC KHÁC MẪU
Quy tắc cộng hai phân thức khác mẫu
Hãy thực hiện các yêu cầu sau để làm phép cộng 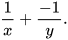
HĐ3 Quy đồng mẫu thức hai phân thức đã cho.
HĐ4 Cộng hai phân thức có cùng mẫu thức nhận được trong HĐ3 ta được kết quả của phép cộng 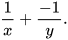
Tổng quát, ta có quy tắc sau:
| Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được. |
Ví dụ 2
Tính tổng 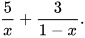
Giải
Quy đồng mẫu hai phân thức đã cho: 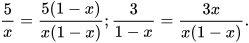
Do đó 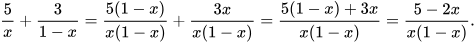
Luyện tập 2 Tính tổng 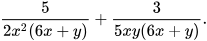
3 TRỪ HAI PHÂN THỨC
Quy tắc trừ hai phân thức
Ở lớp 6, các em đã biết: Để trừ hai phân số cùng mẫu ta trừ các tử và giữ nguyên mẫu; để trừ hai phân số khác mẫu ta quy đồng mẫu hai phân số rồi trừ hai phân số cùng mẫu nhận được. Để trừ hai phân thức, ta cũng làm tương tự như vậy.
HĐ5 Trừ các tử thức và giữ nguyên mẫu thức để tính 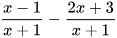 .
.
(Trang 17)
HĐ6 Quy đồng mẫu thức của hai phân thức 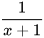 và
và 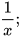 trừ các tử thức của hai phân thức nhận được và giữ nguyên mẫu thức chung để tính
trừ các tử thức của hai phân thức nhận được và giữ nguyên mẫu thức chung để tính 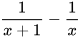 .
.
Tổng quát, ta có quy tắc sau:
| • Muốn trừ hai phân thức có cùng mẫu thức ta trừ các tử thức và giữ nguyên mẫu thức. • Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi trừ các phân thức có cùng mẫu thức vừa tìm được. |
Ví dụ 3 Tính 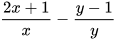 .
.
Giải
Quy đồng mẫu thức hai phân thức đã cho:
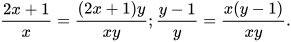
Do đó
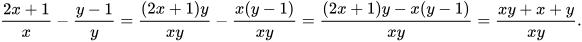
Luyện tập 3 Thực hiện các phép tính sau:
a) 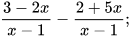 b)
b) 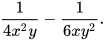
Chú ý. Cũng như phép trừ phân số, ta có thể chuyển phép trừ phân thức thành phép cộng phân thức như sau:
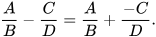
 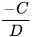 gọi là phân thức đối của phân thức gọi là phân thức đối của phân thức 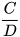 và kí hiệu là và kí hiệu là 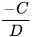 ; tổng ; tổngcủa một phân thức và phân thức đối của nó bằng 0. |
4. CỘNG, TRỪ NHIỀU PHÂN THỨC ĐẠI SỐ
Cách cộng, trừ nhiều phân thức
Vì trừ một phân thức cũng là cộng với phân thức đối của phân thức đó nên các biểu thức gồm các phép tính cộng, trừ phân thức cũng có thể xem là chỉ gồm các phép cộng phân thức. Chẳng hạn, biểu thức 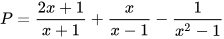 có thể viết thành
có thể viết thành 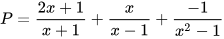 .
.
Cũng như phép cộng phân số, phép cộng phân thức cũng có các tính chất giao hoán, kết hợp. Vì vậy, khi làm tính với một biểu thức chỉ gồm các phép cộng phân thức ta có thể đổi chỗ, nhóm (kết hợp) các số hạng một cách tuỳ ý.
(Trang 18)
Ví dụ 4
Rút gọn biểu thức 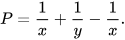
Giải
| Ta có:
| ←Thay phép trừ bằng phép cộng với phân thức đối ← Sử dụng tính chất giao hoán, kết hợp |
Chú ý. Ta cũng có thể viết 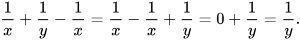
Tổng quát, trong các biểu thức ta có thể đổi chỗ các số hạng kèm theo dấu của nó.
Luyện tập 4 Rút gọn biểu thức 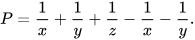
Rút gọn biểu thức có dấu ngoặc
Cũng như khi tính toán với phân số, khi rút gọn một biểu thức có dấu ngoặc, ta có thể bỏ các dấu ngoặc bằng cách sử dụng quy tắc dấu ngoặc sau:
• Nếu trước dấu ngoặc có dấu “+” thì bỏ dấu ngoặc và giữ nguyên các số hạng.
• Nếu trước dấu ngoặc có dấu “-” thì bỏ dấu ngoặc và đổi dấu các số hạng trong dấu ngoặc.
Ví dụ 5
Rút gọn biểu thức 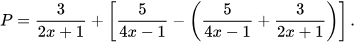
Giải
|
=
= = 0 | ← Trước dấu ngoặc có dấu “-”, đổi dấu các số hạng trong ngoặc ← Trước dấu ngoặc có dấu “+” ← Sử dụng tính chất giao hoán, kết hợp |
Luyện tập 5 Em hãy giải thích cách làm của Vuông trong tình huống mở đầu.
(Trang 19)
Vận dụng
Chú Đức lái ô tô từ Hà Nội về quê. Từ nhà chú đến đường cao tốc dài khoảng 20 km, xe chạy trong thành phố với vận tốc x (km/h). Trên 50 km đường cao tốc, xe tăng vận tốc thêm 55 km/h. Ra khỏi cao tốc, xe còn phải chạy thêm 15 phút thì về đến quê.
a) Viết các phân thức biểu thị thời gian xe chạy trong thành phố và thời gian xe chạy trên đường cao tốc.
b) Viết phân thức biểu thị tổng thời gian chú Đức đi từ Hà Nội về quê.
BÀI TẬP
Trong các bài tập từ 6.20 đến 6.24 dưới đây, hãy thực hiện các phép tính đã chỉ ra.
6. 20
a) 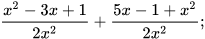 b)
b) 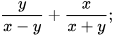 c)
c) 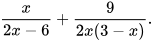
6.21.
a) 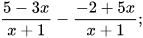 b)
b) 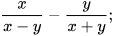 c)
c) 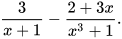
6.22.
a) 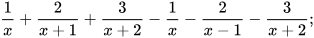
b) 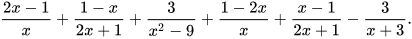
6.23.
a) 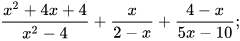
b) 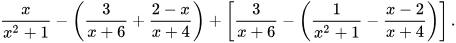
6.24.
a) 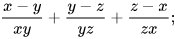
b) 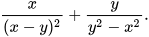
6.25. Một tàu du lịch chạy xuôi dòng 15 km, sau đó quay ngược lại để trở về điểm xuất phát và kết thúc chuyến du lịch. Biết rằng vận tốc của tàu khi nước yên lặng là 10 km/h và vận tốc của dòng nước là x (km/h).
a) Hãy viết các phân thức biểu thị theo x thời gian xuôi dòng, thời gian ngược dòng và tổng thời gian tàu chạy.
b) Tính tổng thời gian tàu chạy khi vận tốc dòng nước là 2 km/h.
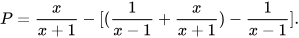
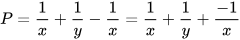
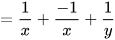
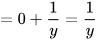 .
.