(Trang 8)
| Khái niệm, thuật ngữ | Kiến thức, kỹ năng |
| - Tính chất cơ bản của phân thức đại số - Mẫu thức chung - Nhân tử phụ - Quy đồng mẫu thức | - Mô tả tính chất cơ bản của phân thức đại số. - Rút gọn phân thức đại số. - Biết quy đồng mẫu thức nhiều phân thức trong trường hợp thuận lợi. |
 Liệu có phân thức nào đơn giản hơn nhưng bằng phân thức
Liệu có phân thức nào đơn giản hơn nhưng bằng phân thức 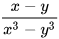 không nhỉ?
không nhỉ?
1 TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
Nhận biết tính chất cơ bản của phân thức đại số
HĐ1 Nếu nhân cả tử và mẫu của phân thức 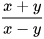 với 2x ta được phân thức mới nào?
với 2x ta được phân thức mới nào?
Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.
HĐ2 Tử và mẫu của phân thức 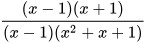 có nhân tử chung là x − 1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó.
có nhân tử chung là x − 1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó.
So sánh phân thức mới nhận được với phân thức đã cho.
Từ HĐ1 và HĐ2, ta thấy phân thức đại số có tính chất cơ bản sau:
• Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân thức bằng phân thức đã cho:
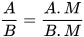 (M là một đa thức khác đa thức 0).
(M là một đa thức khác đa thức 0).
• Nếu tử và mẫu của một phân thức có nhân tử chung thì khi chia cả tử và mẫu cho nhân tử chung đó ta được một phân thức bằng phân thức đã cho:
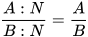 (N là một nhân tử chung).
(N là một nhân tử chung).
(Trang 9)
Ví dụ 1
Dùng tính chất cơ bản của phân thức, giải thích vì sao 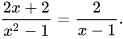
Giải
Áp dụng tính chất cơ bản của phân thức, ta có: 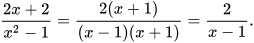
Luyện tập 1 Khẳng định sau đúng hay sai? Vì sao?
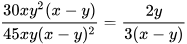 .
.
Luyện tập 2 Giải thích vì sao 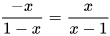 .
.
Chú ý. Tổng quát, ta có quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức bằng phân thức đã cho.
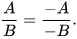
 Đổi dấu một đa thức là đổi dấu tất cả các hạng tử của đa thức đó.
Đổi dấu một đa thức là đổi dấu tất cả các hạng tử của đa thức đó.
2 VẬN DỤNG
a) Rút gọn phân thức
Cách rút gọn một phân thức
Rút gọn một phân thức là biến đổi phân thức đó thành một phân thức mới bằng nó nhưng đơn giản hơn.
Hãy thực hiện các yêu cầu sau đây để rút gọn phân thức 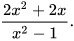
HĐ3 Phân tích tử và mẫu của phân thức 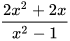 thành nhân tử và tìm các nhân tử chung của chúng.
thành nhân tử và tìm các nhân tử chung của chúng.
HĐ4 Chia cả tử và mẫu của phân thức 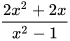 cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn.
cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn.
Muốn rút gọn một phân thức đại số ta làm như sau:
– Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung;
– Chia cả tử và mẫu cho nhân tử chung đó.
Ví dụ 2
Rút gọn phân thức 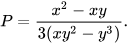
Giải
Ta có: 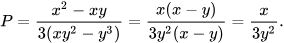
(Trang 10)
Luyện tập 3 Em hãy trả lời câu hỏi trong tình huống mở đầu.
Tranh luận
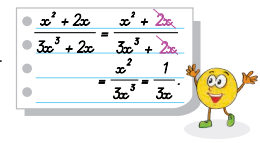
Tròn thực hiện rút gọn một phân thức như hình bên.
Hỏi bạn Tròn làm đúng hay sai? Vì sao?
Thử thách nhỏ
Tìm a sao cho hai phân thức sau bằng nhau:
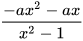 và
và 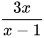 .
.
b) Quy đồng mẫu thức nhiều phân thức
Cách quy đồng mẫu thức nhiều phân thức
Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.
Hãy thực hiện các yêu cầu sau để quy đồng mẫu thức hai phân thức:
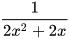 và
và 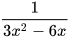 .
.
HĐ5 Phân tích các mẫu thức của hai phân thức đã cho thành nhân tử.
HĐ6 Chọn mẫu thức chung (MTC) của hai mẫu thức trên bằng cách lấy tích của các nhân tử được chọn như sau:
– Nhân tử bằng số của MTC là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số ở MTC là BCNN của chúng);
– Với mỗi luỹ thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn luỹ
thừa với số mũ cao nhất.
HĐ7 Tìm nhân tử phụ của mỗi mẫu thức bằng cách lấy MTC chia cho mẫu thức đó.
HĐ8 Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng, ta được các phân thức có mẫu thức là MTC đã chọn.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
– Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
– Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC cho mẫu thức đó;
– Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
(Trang 11)
Ví dụ 3
Quy đồng mẫu thức hai phân thức 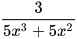 và
và 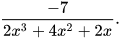
Giải
Ta có: 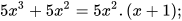
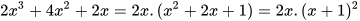 .
.
Mẫu thức chung là 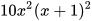 .
.
Nhân tử phụ của 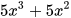 là
là
MTC: 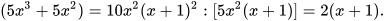
Nhân tử phụ của 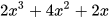 là
là
MTC: 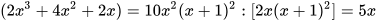 .
.
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
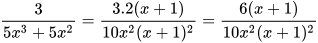 và
và 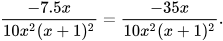
Luyện tập 4
Quy đồng mẫu thức hai phân thức 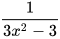 và
và 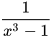
Tranh luận
 Hai phân thức Hai phân thức 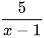 và và 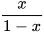 có MTC là x-1. có MTC là x-1. |  Không đúng, MTC là (x − 1)(1 – x) chứ! Không đúng, MTC là (x − 1)(1 – x) chứ! |
Theo em, bạn nào chọn MTC hợp lí hơn? Vì sao?
BÀI TẬP
6.7. Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.
a) 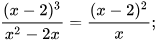 b)
b) 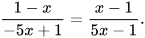
(Trang 12)
6.8. Tìm đa thức thích hợp thay dấu ?
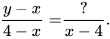
6.9. Rút gọn các phân thức sau:
a) 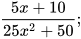 b)
b) 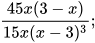 c)
c) 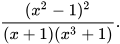
6.10. Cho phân thức 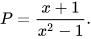
a) Rút gọn phân thức đã cho, kí hiệu Q là phân thức nhận được.
b) Tính giá trị của P và Q tại x= 11. So sánh hai kết quả đó.
6.11. Tìm a sao cho hai phân thức sau bằng nhau:
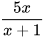 và
và 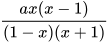 .
.
6.12. Quy đồng mẫu thức các phân thức sau:
a) 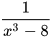 và
và 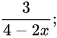 b)
b) 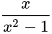 và
và 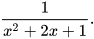
6.13. Quy đồng mẫu thức các phân thức sau:
a) 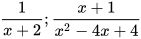 và
và 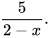 b)
b) 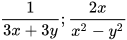 và
và 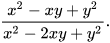
6.14. Cho hai phân thức 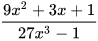 và
và 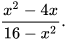
a) Rút gọn hai phân thức đã cho.
b) Quy đồng mẫu thức hai phân thức nhận được ở câu a.