Mở đầu trang 76 Toán 11 Tập 2: Tại vòng chung kết của một đại hội thể thao, vận động viên An thi đấu môn Bắn súng, vận động viên Bình thi đấu môn Bơi lội. Biết rằng xác suất giành huy chương của vận động viên An và vận động viên Bình tương ứng là 0,8 và 0,9. Hỏi xác suất để cả hai vận động viên đạt huy chương là bao nhiêu ?
Lời giải:
Sau bài học, ta trả lời được như sau:
Xác suất để cả hai vận động viên đạt huy chương là: 0,8 . 0,9 = 0,72.
1. Công thức nhân xác suất cho hai biến cố độc lập
HĐ1 trang 76 Toán 11 Tập 2: Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen. Hộp II có 1 quả màu trắng và 7 quả màu đen. Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I, bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II. Xét các biến cố sau:
A: “Bạn Long lấy được quả bóng màu trắng”;
B: “Bạn Hải lấy được quả bóng màu đen”.
a) Tính P(A), P(B) và P(AB).
b) So sánh P(AB) và P(A) . P(B).
Lời giải:
a)
+ Tính P(A):
Biến cố A là tập hợp các quả màu trắng trong 10 quả của hộp I nên n(A) = 6.
Suy ra: P(A) = 6/10.
+ Tính P(B)
Biến cố B là tập hợp các quả màu đen trong 8 quả của hộp II nên n(B) = 7.
Suy ra: P(B) = 7/8.
+ Tính P(AB):
Biến cố C = A ∩ B là biến cố “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”.
Không gian mẫu Ω là tập hợp các cách chọn gồm 2 công đoạn:
Công đoạn 1: Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I.
Có 6 + 4 = 10 (cách chọn).
Công đoạn 2: Bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II.
Có 1 + 7 = 8 (cách chọn)
Theo quy tắc nhân, ta có: n(Ω) = 10 . 8 = 80.
Biến cố C là tập hợp các cách chọn gồm 2 công đoạn:
Công đoạn 1: Bạn Long lấy được quả màu trắng trong hộp I. Có 6 cách chọn.
Công đoạn 2: Bạn Hải lấy được quả màu đen trong hộp II. Có 7 cách chọn.
Theo quy tắc nhân, ta có: n(C) = 6 . 7 = 42.
Suy ra: P(AB) = P(C) = 
b)
Ta có: P(A) . P(B) = 
Như vậy P(A) . P(B) = P(AB).
Câu hỏi trang 76 Toán 11 Tập 2: Hai biến cố A và B trong HĐ1 độc lập hay không độc lập ? Tại sao ?
Lời giải:
Vì Long và Hải lấy bóng từ hai hộp khác nhau nên:
Dù biến cố A có xảy ra hay không ta đều có P(B) 
Dù biến cố B có xảy ra hay không ra đều có P(A) 
Vậy hai biến cố A và B độc lập.
Luyện tập 1 trang 77 Toán 11 Tập 2: Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm.
Lời giải:
Gọi A là biến cố “Hạt giống A nảy mầm”; B là biến cố “Hạt giống B nảy mầm”.
Các biến cố đối 
là biến cố “Hạt giống A không nảy mầm”; 
là “Hạt giống B không nảy mầm”.
Ta có:
P(A) = 0,92. Suy ra P(
) = 1 – 0,92 = 0,08.
P(B) = 0,88. Suy ra P(
) = 1 – 0,88 = 0,12.
Ta có sơ đồ hình cây như sau:
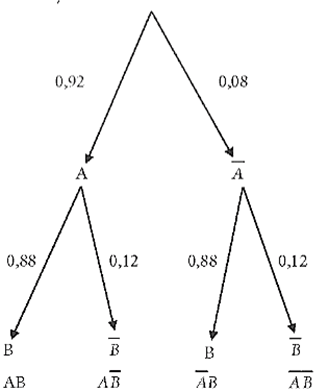
Ta có hai biến cố A và B độc lập.
a)
Biến cố: “Hạt giống A nảy mầm còn hạt giống B không nảy mầm” là biến cố A
Áp dụng công thức nhân xác suất, ta có:
P(A
) = P(A) . P(
) = 0,92 . 0,12 = 0,1104.
b)
Biến cố: “Hạt giống A không nảy mầm còn hạt giống B nảy mầm” là biến cố 
B.
Áp dụng công thức nhân xác suất, ta có:
P(
B) = P(
) . P(B) = 0,08 . 0,88 = 0,0704.
c)
Biến cố: “Có ít nhất một trong hai loại hạt giống nảy mầm” là biến cố A ∪ B.
Áp dụng công thức cộng xác suất và công thức nhân xác suất, ta có:
P(A ∪ B) = P(A) + P(B) – P(AB)
= P(A) + P(B) – P(A) . P(B)
= 0,92 + 0,88 – 0,92 . 0,88
= 0,9904.
Vậy P(A ∪ B) = 0,9904.
2. Vận dụng
Luyện tập 2 trang 78 Toán 11 Tập 2: Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà nghiên cứu chọn một nhóm 5 000 người đàn ông. Với mỗi người trong nhóm, nhà nghiên cứu kiểm tra xem họ có nghiện thuốc lá và có bị viêm phổi hay không. Kết quả được thống kê trong bảng sau:
Từ bảng thống kê trên, hãy chứng tỏ rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.
Lời giải:
Chọn ngẫu nhiên một người đàn ông.
Gọi A là biến cố “Người đó nghiện thuốc lá”,
B là biến cố “Người đó mắc bệnh viêm phổi”.
Khi đó, AB là biến cố “Người đó nghiện thuốc lá và mắc bệnh viêm phổi”.
Do đó, P(AB) ≠ P(A) . P(B) nên hai biến cố A và B không độc lập.
Vậy ta kết luận rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.
