Mở đầu trang 16 Toán 11 Tập 2: Sự tăng trưởng dân số được ước tính theo công thức tăng trưởng mũ sau:
A = Pert,
trong đó P là dân số của năm lấy làm mốc, A là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm. Biết rằng vào năm 2020, dân số Việt Nam khoảng 97,34 triệu người và tỉ lệ tăng dân số là 0,91% (theo danso.org). Nếu tỉ lệ tăng dân số này giữ nguyên, hãy ước tính dân số Việt Nam vào năm 2050.
Lời giải:
Sau bài học, ta giải quyết được bài toán như sau:
Theo bài ra ta có P = 97,34; r = 0,91%.
Từ năm 2020 đến năm 2050 là 30 năm nên t = 30.
Ước tính dân số Việt Nam vào năm 2050 là
A = Pert = 97,34 ∙ e0,91% ∙ 30 ≈ 127,9 (triệu người).
1. Hàm số mũ
HĐ1 trang 16 Toán 11 Tập 2: Nhận biết hàm số mũ
a) Tính y = 2x khi x lần lượt nhận các giá trị – 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của y = 2x tương ứng?
b) Với những giá trị nào của x, biểu thức y = 2x có nghĩa?
Lời giải:
a) Ta có:
+ Với x = – 1 thì y = 2–1 = 1/2
+ Với x = 0 thì y = 20 = 1.
+ Với x = 1 thì y = 21 = 2.
Ta nhận thấy với mỗi giá trị của x có duy nhất một giá trị của y = 2x tương ứng.
b) Biểu thức y = 2x có nghĩa với mọi giá trị của x.
Câu hỏi trang 16 Toán 11 Tập 2: Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ số.
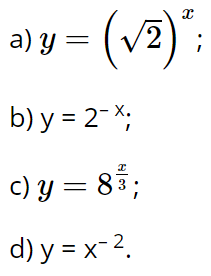
Lời giải:
a) Hàm số 
là hàm số mũ với cơ số √2.
b) Ta có 
. Do đó, hàm số đã cho là hàm số mũ với cơ số 
.
c) Ta có 
. Do đó, hàm số đã cho là hàm số mũ với cơ số 2.
d) Hàm số y = x–2 không phải là hàm số mũ.
HĐ2 trang 16 Toán 11 Tập 2: Nhận dạng đồ thị và tính chất của hàm số mũ
Cho hàm số mũ y = 2x.
a) Hoàn thành bảng giá trị sau:
b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với x ∈ ℝvà nối lại ta được đồ thị của hàm số y = 2x.
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = 2x.
Lời giải:
a) Ta có: 
Vậy ta hoàn thành được bảng đã cho như sau:
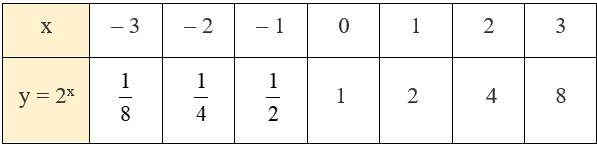
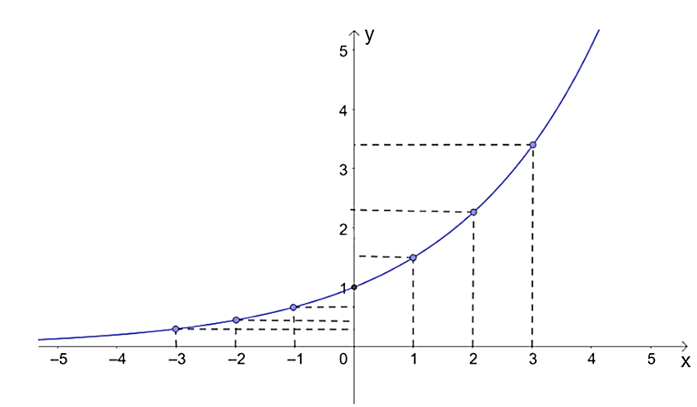
b) Trên mặt phẳng tọa độ Oxy, ta biểu diễn các điểm (x; y) ở câu a và lấy thêm nhiều điểm (x; 2x) với x ∈ ℝ, nối lại ta được đồ thị của hàm số y = 2x như sau:
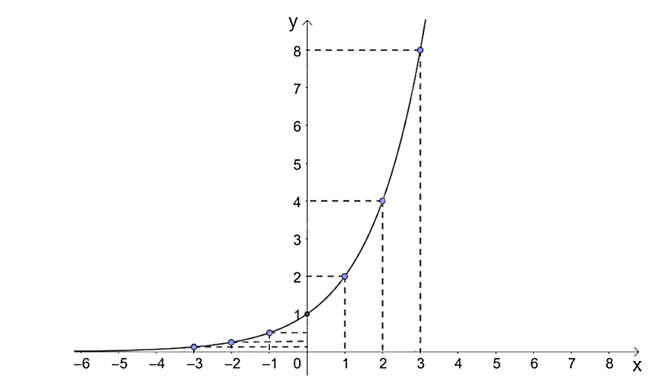
c) Từ đồ thị ở hình trên, ta thấy hàm số y = 2x:
+ Có tập giá trị là (0; + ∞);
+ Đồng biến trên ℝ.
Luyện tập trang 17 Toán 11 Tập 2: Vẽ đồ thị của hàm số 
.
Lời giải:
Ta lập bảng giá trị của hàm số 
tại một số điểm như sau:
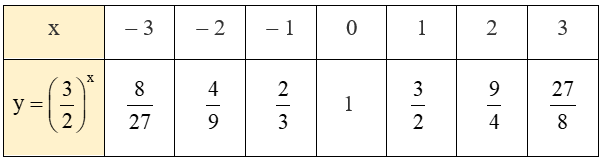
Từ đó, ta vẽ được đồ thị hàm số 
như sau:
2. Hàm số Lôgarit
HĐ3 trang 18 Toán 11 Tập 2: Nhận biết hàm số lôgarit
a) Tính y = log2x khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của y = log2x tương ứng?
b) Với những giá trị nào của x, biểu thức y = log2x có nghĩa?
Lời giải:
a) Ta có:
+ Với x = 1 thì y = log21 = 0;
+ Với x = 2 thì y = log22 = 1;
+ Với x = 4 thì y = log24 = log222 = 2.
Nhận thấy với mỗi giá trị của x > 0 có duy nhất một giá trị của y = log2x tương ứng.
b) Biểu thức y = log2x có nghĩa khi x > 0.
Câu hỏi trang 18 Toán 11 Tập 2: Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số
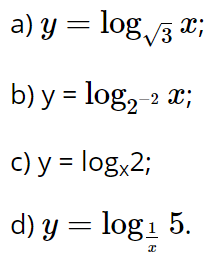
Lời giải:
a) Hàm số 
là hàm số lôgarit với cơ số √3.
b) Ta có 
do đó hàm số đã cho là hàm số lôgarit với cơ số 
c) Hàm số y = logx2 không phải hàm số lôgarit.
d) Hàm số 
không phải hàm số lôgarit.
HĐ4 trang 18 Toán 11 Tập 2: Nhận dạng đồ thị và tính chất của hàm số lôgarit
Cho hàm số lôgarit y = log2x.
a) Hoàn thành bảng giá trị sau:
b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; log2x) và nối lại ta được đồ thị của hàm số y = log2x.
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = log2x.
Lời giải:
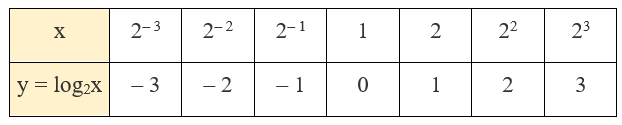
a) Ta có log22–3 = – 3; log22–2 = – 2; log22– 1 = – 1; log21 = 0; log22 = 1; log222 = 2; log223 = 3. Vậy ta hoàn thành được bảng đã cho như sau:
b) Trên mặt phẳng tọa độ Oxy, ta biểu diễn các điểm (x; y) ở câu a và lấy thêm nhiều điểm (x; log2x) với x > 0, nối lại ta được đồ thị của hàm số y = log2x như sau:
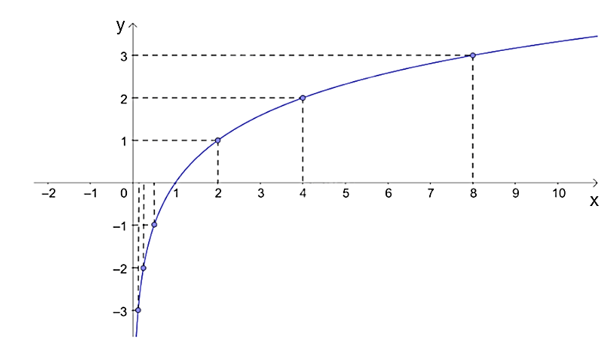
c) Từ đồ thị đã vẽ ở câu b, nhận thấy hàm số y = log2x:
+ Có tập giá trị là ℝ;
+ Đồng biến trên (0; + ∞).
Vận dụng trang 19 Toán 11 Tập 2: Giải bài toán trong tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).
Lời giải:
Theo bài ra ta có P = 97,34; r = 0,91%.
Từ năm 2020 đến năm 2050 là 30 năm nên t = 30.
Ước tính dân số Việt Nam vào năm 2050 là
A = Pert = 97,34 ∙ e0,91% ∙ 30 ≈ 127,9 (triệu người).
