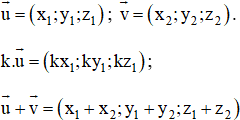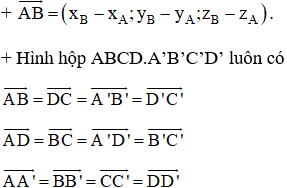Câu hỏi 1 trang 63 SGK
Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto 
theo 3 vectơ không đồng phẳng 
đã cho trên các trục Ox, Oy, Oz.
Lời giải:
Câu hỏi 2 trang 64 SGK
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có 
theo thứ tự cùng hướng với 
và có AB = a, AD = b, AA’ = c. Hãy tính tọa độ các vectơ 
và 
với M là trung điểm của cạnh C’D’.
Lời giải:
Dựa vào đề bài ta có hình vẽ sau:
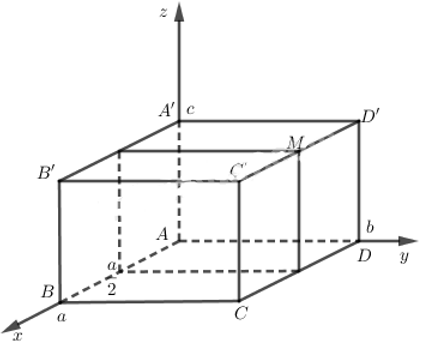
Ta có: A(0; 0; 0) trùng với gốc tọa độ.
Vì B ∈ Ax nên B(a; 0; 0) (trong đó a là độ dài đại số của đoạn AB)
Tương tự ta suy ra các đỉnh D(0; b; 0), A′(0; 0; c)
Điểm C thuộc mp (Axy) nên tọa độ C có dạng (x; y; 0) trong đó x là độ dài đại số của AB, y là độ dài đại số của AD.
Suy ra C (a; b; 0)
Tương tự ta suy ra D′(0; b; c), B′(a; 0; c), C′(a; b; c), M (a/2; b; c).
Từ đó, suy ra tọa độ các vectơ là:
Câu hỏi 3 trang 66 SGK
Với hệ tọa độ Oxyz trong không gian, cho 
Hãy tính 
Lời giải:
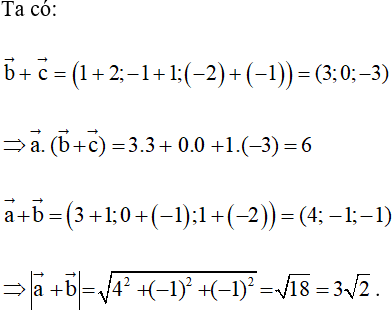
Câu hỏi 4 trang 67 SGK
Viết phương trình mặt cầu tâm I (1; -2; 3) có bán kính r = 5.
Lời giải:
Phương trình mặt cầu là: (x – 1)2 + (y + 2)2 + (z – 3)2 = 52
Bài 1 trang 68 SGK
Cho ba vectơ: 
a) Tính tọa độ của vectơ 
b) Tính tọa độ của vectơ 
Lời giải:
Kiến thức áp dụng
Trong hệ trục tọa độ không gian Oxyz:
Bài 2 trang 68 SGK
Cho ba điểm A(1; -1; 1), B(0; 1; 2), C(1; 0; 1). Tìm tọa độ trọng tâm G của tam giác ABC.
Lời giải:
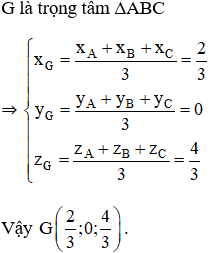
Bài 3 trang 68 SGK
Cho hình hộp ABCD.A'B'C'D' biết A = (1; 0; 1), B = (2; 1; 2), D = (1; –1; 1), C' = (4; 5; –5). Tính tọa độ các đỉnh còn lại của hình hộp.
Lời giải:
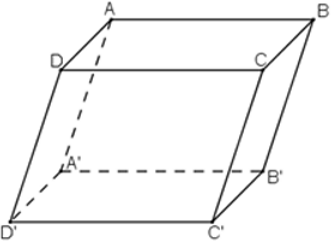
Ta có: 
Vì ABCD là hình bình hành nên theo quy tắc hình bình hành:
⇒ C = (2; 0; 2)
⇒ 
Vì ABCD.A'B'C'D' là hình hộp nên: 
Kiến thức áp dụng
Bài 4 trang 68 SGK
Tính
Lời giải:
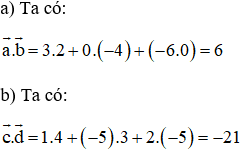
Kiến thức áp dụng
Tích vô hướng của hai vec tơ
và
là:
Bài 5 trang 68 SGK
Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:
a) x2 + y2 + z2 – 8x – 2y + 1 = 0
b) 3x2 + 3y2 + 3z2 – 6x + 8y + 15z – 3 = 0
Lời giải:
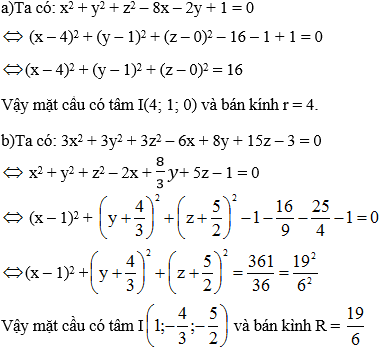
Kiến thức áp dụng
Mặt cầu tâm I (a; b; c), bán kính R có phương trình:
(x – a)2 + (y – b)2 + (z – c)2 = R2
⇔ x2 + y2 + z2 – 2ax – 2by – 2cz + a2 + b2 + c2 – R2 = 0
Bài 6 trang 68 SGK
Lập phương trình mặt cầu trong hai trường hợp sau đây:
a) Có đường kính AB với A = (4; –3; 7), B = (2; 1; 3).
b) Đi qua điểm A = (5; –2; 1) và có tâm C = (3; –3; 1).
Lời giải:
a) Gọi I là tâm mặt cầu.
Suy ra, I là trung điểm AB (do AB là đường kính).
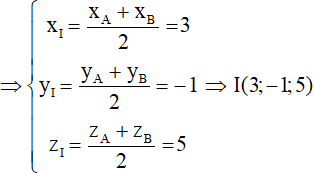
Bán kính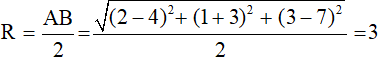 
Vậy phương trình mặt cầu là:
(x – 3)2 + (y + 1)2 + (z – 5)2 = 9.
b) Vì A nằm trên mặt cầu có tâm C nên bán kính
R = CA = 
Phương trình mặt cầu là:
(x – 3)2 + (y + 3)2 + (z – 1)2 = 5.
