Câu hỏi 1 trang 15 SGK
Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.
Lời giải:
Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic
Khối đa diện không lồi trong thực tế: cái bàn
Câu hỏi 2 trang 16 SGK
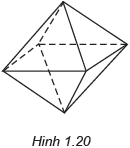
Đếm số đỉnh, số cạnh của khối bát diện đều.
Lời giải:
Khối bát diện đều có 6 đỉnh và 12 cạnh.
Câu hỏi 3 trang 17 SGK
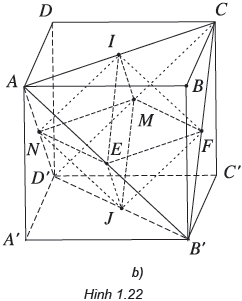
Chứng minh rằng AB’CD’.A’B’C’D’ có cạnh bằng a (h.1.22b).
Lời giải:
ABCD.A’B’C’D’ là hình lập phương cạnh a nên các mặt là các hình vuông cạnh a.
Tứ diện AB’CD’ có các cạnh là các đường chéo của các mặt bên hình lập phương ABCD.A’B’C’D’ nên tứ diện AB’CD’ có các cạnh bằng nhau.
Do đó: AB’CD’ là tứ diện đều.
Cạnh của tứ diện đều AB’CD’ bằng độ dài đường chéo của hình vuông cạnh a và bằng √(a2 + a2) = a√2
Câu hỏi 4 trang 18 SGK
Chứng minh rằng AB′CD′ là một tứ diện đều. Tính các cạnh của nó theo a.
Gọi I, J, E, F, M và N lần lượt là tâm của các mặt ABCD, A'B'C'D', ABB'A', BCC'B', CDD'C' và DAA'D' của hình lập phương. Để ý rằng sáu điểm trên cũng lần lượt là trung điểm của các cạnh AC, B'D', AB', B'C, CD' vμ D'A của tứ diện đều AB'CD' nên theo câu a) sáu điểm đó là các đỉnh của hình bát diện đều.
Lời giải:
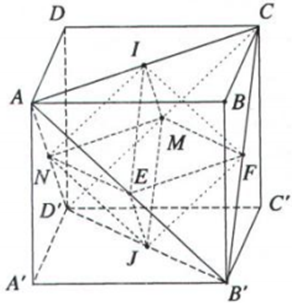
ABCD.A′B′C′D′ là hình lập phương cạnh a nên các mặt là các hình vuông cạnh a.
Tứ diện AB′CD′ có các cạnh là các đường chéo của các mặt bên hình lập phương ABCD.A′B′C′D′ nên tứ diện AB′CD′ có các cạnh bằng nhau.
⇒ AB′CD′ là tứ diện đều.
Cạnh của tứ diện đều AB′CD′ bằng độ dài đường chéo của hình vuông cạnh a và bằng a√2.
Bài 1 trang 18 SGK
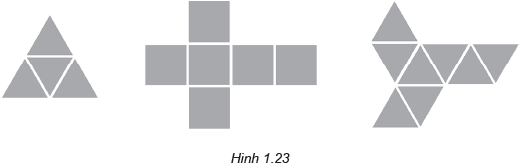
Cắt bìa theo mẫu dưới đây (h.123), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập phương và hình bát diện đều.
Lời giải:
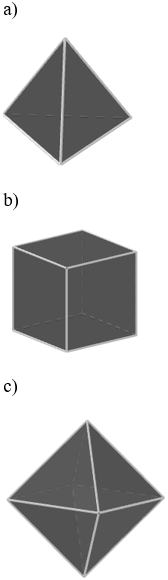
Bài 2 trang 18 SGK
Cho hình lập phương (H). Gọi (H’) là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H’).
Lời giải:
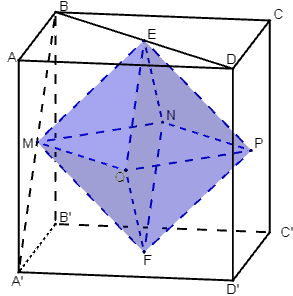
Gọi a là cạnh của hình lập phương ABCD.A’B’C’D’ (hình (H)).
Suy ra diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).
Gọi tâm các mặt của hình lập phương ABCD.A’B’C’D’ lần lượt là E, F, M, N, P, Q như hình vẽ.
Suy ra (H’) là bát diện đều EMNPQF.
+ Áp dụng định lí Pytago vào tam giác vuông AA’D ⇒ A’D = a√2
+ EM là đường trung bình của ΔBA’D
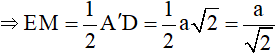
⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng a/√2
⇒ Diện tích một mặt của (H’) là:
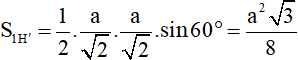
⇒ Diện tích toàn phần của (H’) là:
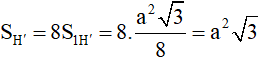
Vậy tỉ số diện tích cần tính là:
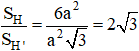
Bài 3 trang 18 SGK
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Lời giải:
Gọi A′, B′, C′, D′ lần lượt là trọng tâm của các tam giác đều BCD, ACD, ABD, ABC.
Gọi M là trung điểm BC.
Ta có: MD′/MA = MA′/MD = 1/3 (tính chất đường trung tuyến).
⇒ A′D′//AD (định lý Ta-lét).
và A′D′ = (1/3)AD = a/3
Tương tự A′B′= B′C′ = C′A′ = B′D′ = C′D′ = a/3
Vậy A′B′C′D′ là tứ diện đều.
Bài 4 trang 18 SGK
Chứng minh rằng:
a) Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
b) ABFD, AEFC và BCDE là những hình vuông.
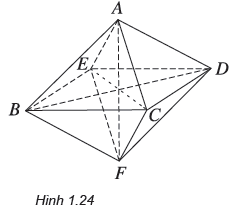
Lời giải:
Giả sử bát diện đều ABCDEF có cạnh bằng a.
a) B, C, D, E cách đều A và F suy ra B, C, D, E cùng nằm trên mặt phẳng trung trực của đoạn thẳng AF
Trong mặt phẳng (BCDE), ta có BC = CD = DE = EB (= a)
Suy ra BCDE là hình thoi.
Suy ra BD ⊥ EC và BD, EC cắt nhau tại trung điểm mỗi đường.
Chứng minh tương tự ta suy ra AF và BD, AF và CE vuông góc nhau và cắt nhau tại trung điểm mỗi đường.
Vậy các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
b) Gọi trung điểm BD, CE, AF là O.
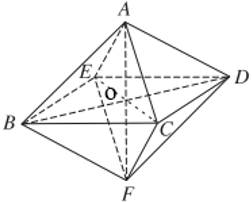
Khi đó áp dụng định lý Py – ta – go ta có:
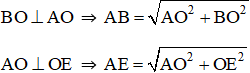
Mà AB = AE (= a) ⇒ BO = OE ⇒ BD = EC
Do đó hình thoi BCDE là hình vuông.
Chứng minh tương tự: ABFD, AEFC đều là hình vuông.



































