Câu hỏi 1 trang 22 SGK
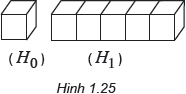
Có thể chia (H1) thành bao nhiêu khối lập phương bằng (H0)?
Lời giải:
Có thể chia (H1) thành 5 khối lập phương (H0).
Câu hỏi 2 trang 22 SGK
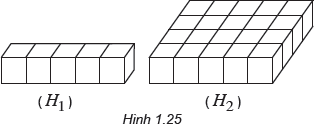
Có thể chia (H2) thành bao nhiêu khối hộp chữ nhật bằng (H1)?
Lời giải:
Có thể chia (H2) thành 4 khối hộp chữ nhật (H1).
Câu hỏi 3 trang 22 SGK
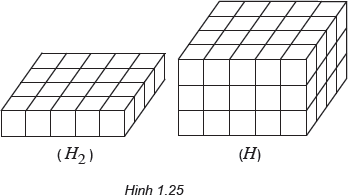
Có thể chia (H) thành bao nhiêu khối hộp chữ nhật bằng (H2) ?...
Lời giải:
Có thể chia (H) thành 3 khối hộp chữ nhật (H2).
Câu hỏi 4 trang 24 SGK
Kim tự tháp Kê-ốp ở Ai Cập (h.1.27) được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Hãy tính thể tích của nó.

Lời giải:
Kim tự tháp là khối chóp tứ giác đều nên đáy là hình vuông có cạnh 230 m.
Diện tích đáy là:
230.230 = 52 900 (m2).
Thể tích kim tự tháp Kê-ốp là:
V = (1/3).52900.147 = 2592100 (m3).
Bài 1 trang 25 SGK
Tính thể tích khối tứ diện đều cạnh a.
Lời giải:
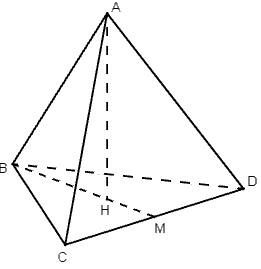
Gọi ABCD là tứ diện đều cạnh a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)
Lại có: AB = AC = AD vì ABCD là tứ diện đều
⇒ HA là trục đường tròn ngoại tiếp tam giác BCD
⇒ HA ⊥ (BCD)
Vì tam giác BCD là tam giác đều nên H đồng thời trọng tâm tam giác BCD. Gọi M là trung điểm của CD.
Xét tam giác BCD ta có:
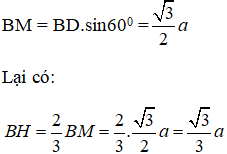
Áp dụng định lí pytago vào tam giác vuông AHB ta được:
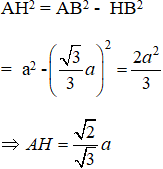
Diện tích tam giác đều BCD cạnh a là:
![]()
Do đó, thể tích khối tứ diện đều ABCD là:
![]()
Kiến thức áp dụng
+ Thể tích khối chóp có diện tích đáy B và chiều cao h là:
+ Diện tích tam giác đều cạnh a là:
Bài 2 trang 25 SGK
Tính thể tích khối bát diện đều cạnh a.
Lời giải:
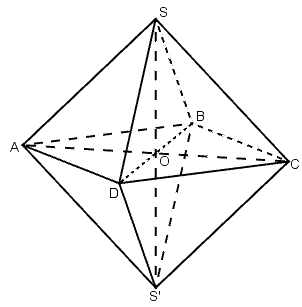
Gọi khối bát diện đều là SABCDS’ cạnh a.
* Ta chia khối bát diện thành hai khối chóp tứ giác đều bằng nhau là:
S. ABCD và S’. ABCD có cạnh bằng a.
Khi đó, VSABCDS’ = VS.ABCD + VS’.ABCD = 2.VS.ABCD
Gọi O là giao điểm của AC và BD suy ra: SO ⊥ (ABCD)
* Ta tính thể tính khối tứ diện đều cạnh a.
Tứ giác ABCD là hình vuông cạnh a nên có diện tích là: SABCD = a2
Ta có:
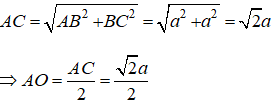
Áp dụng định lí pytago vào tam giác SOA ta có:
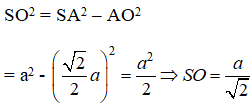
Thể tích khối tứ diện đều S.ABCD là:
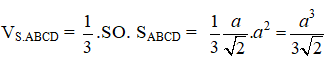
Thể tích khối bát diện đều cạnh a là:
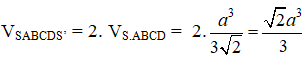
Bài 3 trang 25 SGK
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Lời giải:
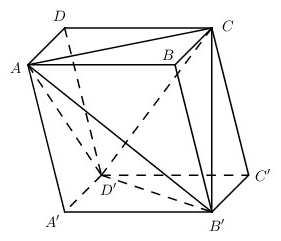
Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp thì thể tích của khối hộp.
⇒ V = S.h
Chia khối hộp thành khối tứ diện ACB′D′ và bốn khối chóp A.A′B′D′, C.C′B′D′, B′.BAC và D′.DAC.
Xét khối chóp A.A′B′D′ có diện tích đáy SA′B′D′ = S/2 và chiều cao bằng h.
Do đó:
Tương tự như vậy ta chứng minh được:
Vậy VACB′D′ = V − (VA.A′B′D′ + VC.C′B′D′ + VB′BAC + VD′.DAC)
Bài 4 trang 25 SGK
Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng:
Lời giải:
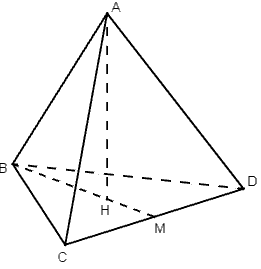
Gọi H và K lần lượt là hình chiếu vuông góc của A và A’ trên mp(SBC),
Đặt AH = h1 và A’K = h2 ,
S1 và S2 lần lượt là diện tích của hai tam giác SBC và SB’C’.
* Do A’K// AH nên bốn điểm A, A’; K và H đồng phẳng. (1)
Lại có, 3 điểm A, S, H đồng phẳng (2).
Từ (1) và (2) suy ra, 5 điểm A, A’, S. H và K đồng phẳng.
Trong mp(ASH) ta có: 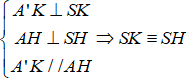
⇒ Ba điểm S, H và K thẳng hàng.
* Ta có:
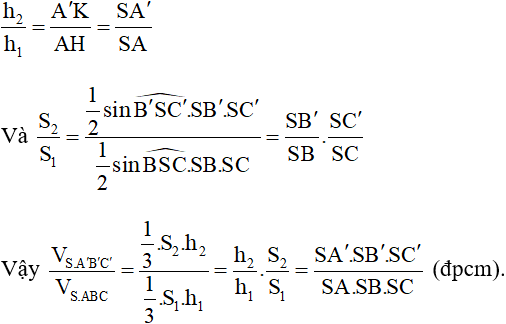
Bài 5 trang 26 SGK
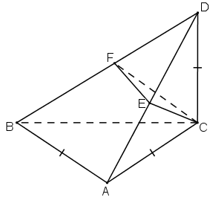
Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua C, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
Lời giải:


Bài 6 trang 26 SGK
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Lời giải:

Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và 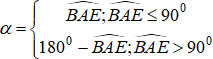
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
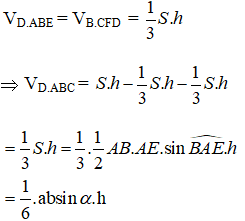
Do đó, thể tích khối tứ diện ABCD không đổi.



































