Bài 1 trang 27 SGK
Trong số các mệnh đề sau, mệnh đề nào đúng?
(A) Số đỉnh và số mặt của một hình đa diện luôn bằng nhau;
(B) Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau;
(C) Tồn tại một hình đa diện có số cạnh bằng số đỉnh;
(D) Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau.
Lời giải:
Hình lập phương có 8 đỉnh và 6 mặt nên đáp án A sai.
Xét hình tứ diện có 4 đỉnh và 4 mặt, nên đáp án B đúng.
Giả sử khối đa diện có số cạnh bằng số đỉnh ⇒ Đ = C ⇒ p = 2, tức là mỗi mặt có 2 cạnh (vô lí). Do đó đáp án C sai.
Giả sử khối đa diện có số cạnh bằng số mặt ⇒ M = C ⇒ n = 2, tức là mỗi đỉnh là đỉnh chung của 2 cạnh (vô lí). Do đó đáp án D sai.
Chọn (B).
Bài 2 trang 27 SGK
Trong các mệnh đề sau, mệnh đề nào đúng?
Số các đỉnh hoặc số các mặt của bất kì hình đa diện nào cũng:
(A) Lớn hơn hoặc bằng 4; (B) Lớn hơn 4;
(C) Lớn hơn hoặc bằng 5; (D) Lớn hơn 5.
Lời giải:
Chú ý: Đa giác là một đường gấp khúc khép kín, nghĩa là gồm những đoạn thẳng nối tiếp nhau (mỗi điểm nối là đầu mút của vừa đúng hai đoạn thẳng) cùng nằm trên một mặt phẳng và khép kín.
Hình đa diện là một số hữu hạn đa giác thỏa mãn hai điều kiện:
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Như vậy để tạo thành một hình đa diện ta cần ít nhất 3 điểm (tạo thành 1 mặt phẳng) và 1 điểm nằm ngoài mặt phẳng ấy.
Với 4 điểm này, tạo thành một hình tứ diện có 4 đỉnh và 4 mặt.
Dễ thấy hình tứ diện là hình đa diện có số mặt và số đỉnh nhỏ nhất trong các khối đa diện.
Chọn (A).
Bài 3 trang 27 SGK
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) Lớn hơn hoặc bằng 6;
(B) Lớn hơn 6;
(C) Lớn hơn 7;
(D) Lớn hơn hoặc bằng 8.
Lời giải:
Chú ý: Hình đa diện là một số hữu hạn đa giác thỏa mãn hai điều kiện:
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Như vậy để tạo thành một hình đa diện ta cần ít nhất 3 điểm (tạo thành 1 mặt phẳng) và 1 điểm nằm ngoài mặt phẳng ấy.
Với 4 điểm này, tạo thành một hình tứ diện có 4 đỉnh, 4 mặt và 6 cạnh.
Dễ thấy hình tứ diện là hình đa diện có số cạnh nhỏ nhất trong các khối đa diện.
Chọn (A).
Bài 4 trang 28 SGK
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Khối tứ diện là khối đa diện lồi;
(B) Khối hộp là khối đa diện lồi;
(C) Lắp ghép hai khối hộp sẽ được một khối đa diện;
(D) Khối lăng trụ tam giác là khối đa diện lồi.
Lời giải:
Dễ dàng nhận thấy các khối tứ diện, khối hộp, khối lăng trụ tam giác là các khối đa diện lồi. Do đó A, B, D đúng.
Khi lắp ghép hai khối hộp chưa chắc được một đa diện lồi. Ví dụ khi lắp ghép hai khối hộp như sau, ta không được một khối đa diện lồi.
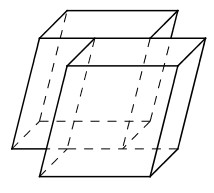
Chọn (C).
Bài 5 trang 28 SGK
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
(B) Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
(C) Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
(D) Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
Lời giải:
• Ta có: Vchóp = (1/3).Sđáy.h nên đương nhiên khi hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau nên A đúng.
• Ta có: Vlăng trụ = Sđáy.h nên đương nhiên khi hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau nên C đúng.
• Diện tích toàn phần của khối lập phương cạnh a: Stp = 6a2, hai khối lập phương có diện tích toàn phần bằng nhau tức là có cạnh bằng nhau nên Vlập phương = a3, vậy chúng có thể tích bằng nhau nên D đúng.
• Hai khối chóp cụt có diện tích một đáy bằng nhau, chiều cao bằng nhau nhưng đáy còn lại có diện tích khác nhau thì thể tích khác nhau.
Chọn (B).
Bài 6 trang 28 SGK
Cho hình chóp S.ABC. Gọi A' và B' lần lượt là trung điểm của SA và SB. Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC bằng:
(A) 1/2;
(B) 1/3;
(C) 1/4;
(D) 1/8.
Lời giải:
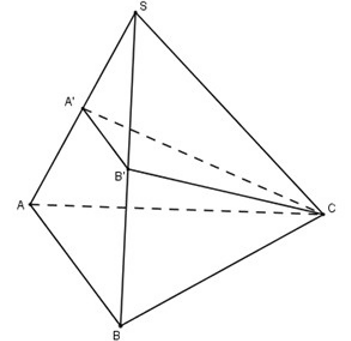
Ta có:
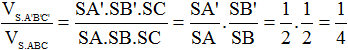
Chọn (C).
Bài 7 trang 28 SGK
Cho hình chóp S.ABCD. Gọi A', B', C', D' theo thứ tự là trung điểm của SA, SB, SC, SD. Tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD bằng:
(A) 1/2;
(B) 1/4;
(C) 1/8;
(D) 1/16.
Lời giải:
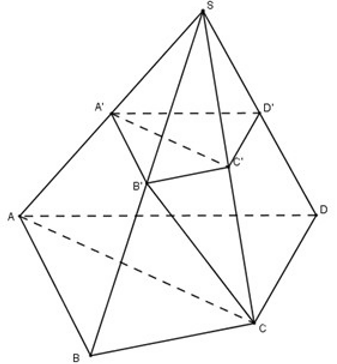
Vì công thức tỉ số thể tích chỉ dùng cho hình chóp tam giác, nên ta chia hình chóp tứ giác S.A’B’C’D’ thành hai hình chóp tam giác S.A’B’C’ và S.A’C’D’ và chia hình chóp S.ABCD thành hai hình chóp S.ABC và S.ADC.

Chọn (C).
Bài 8 trang 28 SGK
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là:
![]()
Lời giải:
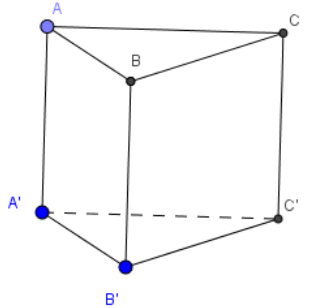
Vì đây là hình lăng trụ đều có tất cả các cạnh bằng a nên đáy của hình lăng trụ là tam giác đều và cạnh bên vuông góc với đáy.
⇒ Diện tích đáy của hình lăng trụ là: ![]()
Thể tích của khối lăng trụ cần tính là:
![]()
Chọn (D).
Bài 9 trang 28 SGK
Cho hình hộp ABCD.A’B’C’D’. Tỉ số thể tích của khối tứ diện ACB’D’ và khối hộp ABCD.A’B’C’D’ bằng:
(A) 1/2;
(B) 1/3;
(C) 1/4;
(D) 1/6.
Lời giải:
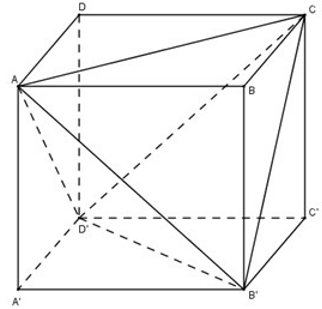
Gọi S là diện tích đáy và h là chiều cao của hình lăng trụ ABCD.A’B’C’D’.
Khi đó, thể tích của hình hộp đã cho là: V = S.h
Ta chia hình hộp đã cho thành 5 khối tứ diện là: B’ABC, AA’B’D’; CB’C’D’; D’ADC và ACB’D’.
Mỗi khối tứ diện B’ABC, AA’B’D’; CB’C’D’; D’ADC có thể tích bằng:
![]()
Do đó, thể tích khối tứ diện ACB’D’ là:
![]()
Suy ra, tỉ số thể tích của hai khối tứ diện ACB’D’ và ABCD. A’B’C’D’ là:
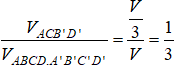
Chọn (B).
Bài 10 trang 28 SGK
Cho hình hộp ABCD.A’B’C’D’, gọi O là giao của AC và BD. Tỉ số thể tích của khối chóp O.A’B’C’D’ và khối hộp ABCD.A’B’C’D’ bằng:
(A) 1/2;
(B) 1/3;
(C) 1/4;
(D) 1/6.
Lời giải:
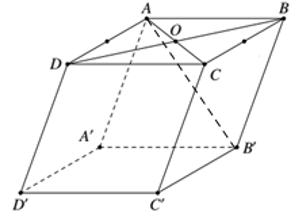
Khối chóp O.A’B’C’D’ và khối hộp ABCD.A’B’C’D’ có cùng chiều cao, ta gọi chiều cao đó là h.
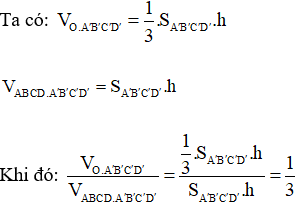
Chọn (B).



































