Câu hỏi 1 trang 43 SGK
Tìm tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước...
Lời giải:
Tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước là đường trung trực của đoạn thẳng AB
Câu hỏi 2 trang 45 SGK
a) Hãy xác định đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng r/2.
b) Cho mặt cầu S(O; r), hai mặt phẳng (α) và (β) có khoảng cách đến tâm O của mặt cầu đã cho lần lượt là a và b (0 < a < b < r). Hãy so sánh hai bán kính của các đường tròn giao tuyến.
Lời giải:
a) Đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) là đường tròn tâm H:
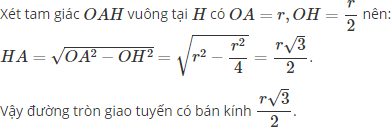
b)
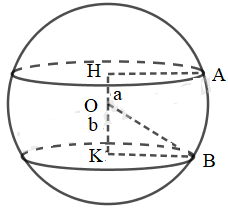
Xét tam giác OHA vuông tại H ta có:
![]()
Xét tam giác OKB vuông tại K ta có:
![]()
Mà 0 < a < b < r nên 0 < r2 – b2 < r2 – a2
⇒ ![]() hay KB < HA.
hay KB < HA.
Vậy đường tròn cắt bởi (β) có bán kính nhỏ hơn bán kính đường tròn cắt bởi (α).
Câu hỏi 3 trang 48 SGK
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
a) Đi qua 8 đỉnh của hình lập phương.
b) Tiếp xúc với 12 cạnh của hình lập phương.
c) Tiếp xúc với 6 mặt của hình lập phương.
Lời giải:
a) Tâm O của mặt cầu là giao điểm của các đường chéo:
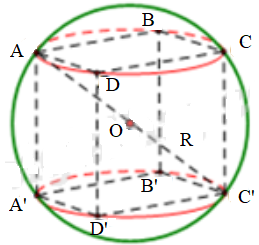
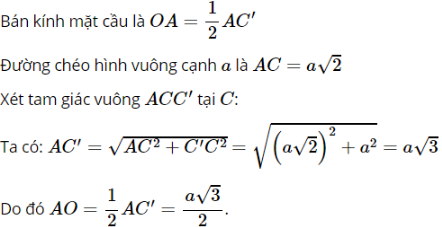
Vậy bán kính mặt cầu đi qua 8 đỉnh hình lập phương cạnh a là ![]()
b) Không có mặt cầu tiếp xúc với 12 cạnh của hình lập phương
c) Tâm mặt cầu tiếp xúc 6 mặt của hình lập phương là trung điểm I của đường nối hai tâm đáy.
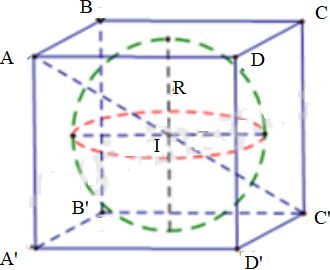
Bán kính mặt cầu là ![]()
Câu hỏi 4 trang 48 SGK
Cho hình lập phương ngoại tiếp mặt cầu bán kính r cho trước. Hãy tính thể tích của hình lập phương đó.
Lời giải:
Ta có thể lấy hình vẽ của phần c) ở câu hỏi trên:
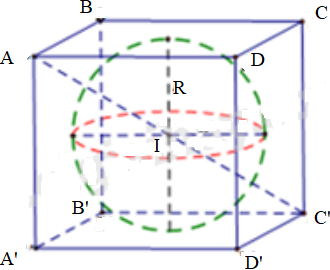
Hình lập phương ngoại tiếp mặt cầu bán kính r có cạnh bằng 2r
Thể tích hình lập phương đó là: V = (2r)3 = 8r3
Bài 1 trang 49 SGK
Tìm tập hợp tất cả các điểm M trong không gian luôn luôn nhìn một đoạn thẳng AB cố định dưới một góc vuông.
Lời giải:
+ Gọi O là trung điểm của AB.
Tam giác AMB là vuông tại M có OM là đường trung tuyến ứng với cạnh huyền nên: ![]()
Suy ra, M thuộc mặt cầu tâm O, bán kính là ![]()
+ Ngược lại, xét mặt cầu ![]() với O là trung điểm của AB.
với O là trung điểm của AB.
![]()
Lấy điểm M bất kì thuộc mặt cầu này. Suy ra: ![]() (2)
(2)
Từ (1) và (2) suy ra:
![]()
⇒ Tam giác MAB vuông tại M.
Kết luận: Vậy tập hợp các điểm M trong không gian luôn nhìn đoạn thẳng AB cố định dưới 1 góc vuông là mặt cầu ![]()
Bài 2 trang 49 SGK
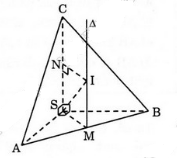
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Lời giải:
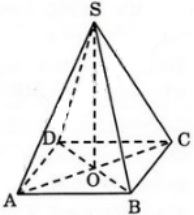
S.ABCD là hình chóp tứ giác đều cạnh đều bằng a.
⇒ ABCD là hình vuông cạnh a và SA = SB = SC = SD = a.
Gọi O là hình chiếu của S trên (ABCD).
⇒ O là tâm hình vuông ABCD.
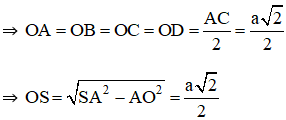
⇒ OA = OB = OC = OD = OS.
⇒ O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính mặt cầu là ![]()
Bài 3 trang 49 SGK
Tìm tập hợp tâm các mặt cầu luôn luôn chứa một đường tròn cố định cho trước.
Lời giải:
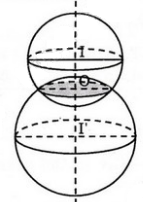
Gọi I là tâm của mặt cầu chứa đường tròn (C) cố định cho trước.
⇒ I cách đều tất cả các điểm M thuộc đường tròn (C).
⇒ I nằm trên đường thẳng đi qua tâm của đường tròn (C) và vuông góc với mặt phẳng chứa (C).
Bài 4 trang 49 SGK
Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Lời giải:
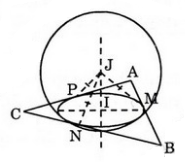
* Xét mặt cầu (S) tâm J, bán kính R và tiếp xúc với ba cạnh: AB, BC, AC lần lượt tại M, N và P.
Gọi I là hình chiếu vuông góc của J lên mp (ABC) ⇒ IJ ⊥ (ABC)
* Ta có: ![]() (định lí 3 đường vuông góc)
(định lí 3 đường vuông góc)
Chứng minh tương tự có: ![]() (1)
(1)
* Xét ba tam giác JIM; JIN và JIP có:
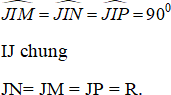
⇒ ∆ JIM = ∆ JIN = ∆JIP (ch- cgv)
⇒ IN = IM = IP (2)
Từ (1) và (2) suy ra, I là tâm đường tròn nội tiếp tam giác ABC.
* Lấy điểm J thuộc trục đường tròn nội tiếp tam giác ABC.
Đường tròn nội tiếp tam giác ABC tiếp xúc với ba cạnh AB, BC và CA lần lượt taị M, N và P.
Ta có: ![]()
Mặt khác; IM = IN = IP = r.
⇒ ∆ JIM = ∆ JIN = ∆JIP (c-g-c)
⇒ JM = JN = JP (2)
Từ (1) và (2) suy ra, mặt cầu (S) tâm J tiếp xúc với ba cạnh của tam giác ABC.
Vậy tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là trục đường tròn nội tiếp tam giác ABC.
Bài 5 trang 49 SGK
Từ một điểm M nằm nằm bên ngoài mặt cầu S( O; r) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
a) Chứng minh rằng MA.MB = MC.MD
b) Gọi MO = d. Tính MA.MB theo R và d.
Lời giải:
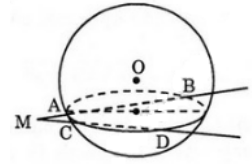
a) Gọi (P) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng(P) cắt mặt cầu S(O; r) theo một đường tròn tâm I, là hình chiếu vuông góc của O lên mặt phẳng (P).
Xét hai tam giác MAD và MCB có:

⇒ MA.MB = MC.MD (đpcm).
b) Giả sử đường thẳng MO cắt mặt cầu tại P và Q.
Theo kết quả phần a) ta cùng có:
MA.MB = MP.MQ
Mà MP.MQ = (MO – OP)(MO + OQ) = (d – r)(d + r) = d2 – r2.
Vậy MA.MB = d2 – r2.
Bài 6 trang 49 SGK
Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)
Lời giải:
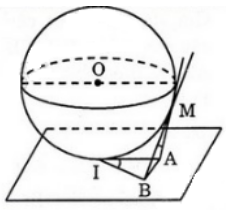
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB (c.c.c)
![]()
Bài 7 trang 49 SGK
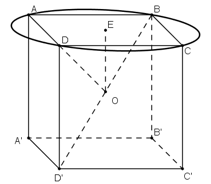
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
Lời giải:

Bài 8 trang 49 SGK
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng độ dài của các cặp cạnh đối diện tứ diện bằng nhau.
Lời giải:
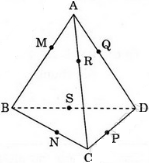
Gọi mặt cầu S(O; R) tiếp xúc với các cạnh của hình tứ diện đã cho lần lượt tại M, N, P, Q ,R và S.
* Ta chứng minh: AM = AR = AQ.
Do mặt cầu tiếp xúc với ba cạnh AB, AC và AD lần lượt tại M; R và Q nên :
![]()
Xét ba tam giác OAM; OAR và OAQ có:
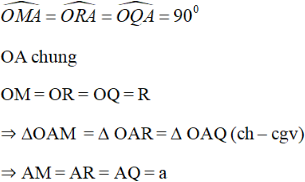
* Chứng minh tương tự ta có:
BM = BN = BS = b
CP = CN = CR = c.
DP = DQ = DS = d
Ta có:
Do đó, AB + CD = AC + BD = AD + BC.
Bài 9 trang 49 SGK
Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định
Lời giải:
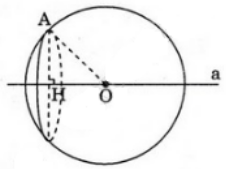
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
Bài 10 trang 49 SGK
Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Lời giải:
* Gọi M là trung điểm của tam giác SAB.
Tam giác SAB là tam giác vuông tại S có SM là đường trung tuyến nên ta có:
![]()
⇒ M là tâm đường tròn ngoại tiếp tam giác SAB.
* Kẻ Mt ⊥ (SAB), ta có: Mt// SC và Mt là trục đưởng tròn ngoại tiếp tam giác SAB.
Trong mp(Mt, SC), đường trung trực của SC cắt Mt tại điểm I.
Ta có: IS = IC. (1)
Và IS = IB = IA (2).
Từ (1) và (2) suy ra: IA = IB= IC = IS
Do đó, I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
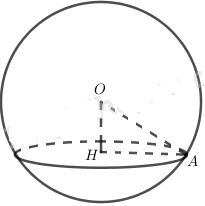
Bán kính mặt cầu ngoại tiếp hình chóp là: