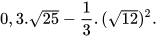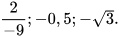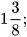(Trang 38)
 | Các số hữu tỉ và vô tỉ được gọi chung là số gì? |
I. TẬP HỢP SỐ THỰC
1. Số thực
1
a) Nêu hai ví dụ về số hữu tỉ.
b) Nếu hai ví dụ về số vô tỉ.
|
Số hữu tỉ và số vô tỉ được gọi chung là số thực. Tập hợp các số thực được kí hiệu là R. |
2. Biểu diễn thập phân của số thực
2
a) Nếu biểu diễn thập phân của số hữu tỉ.
b) Nêu biểu diễn thập phân của số vô tỉ.
Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Cụ thể, ta có sơ đồ sau:
| Số thực | |
| Số hữu tỉ | Số vô tỉ |
| Biểu diễn bằng số thập phân hữu hạn hoặc vô hạn tuần hoàn | Biểu diễn bằng số thập phân vô hạn không tuần hoàn |
(Trang 39)
II. BIỂU DIỄN SỐ THỰC TRÊN TRỤC SỐ
3) Biểu diễn các số hữu tỉ sau trên trục số: 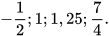
Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x
Ví dụ 1 Biểu diễn số thực 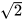 trên trục số.
trên trục số.
Giải
Để biểu diễn số thực 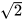 trên trục số, ta làm như sau:
trên trục số, ta làm như sau:
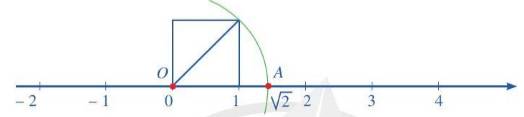
– Vẽ hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài bằng 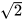 .
.
– Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là 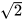 , cắt trục số tại điểm A nằm bên phải điểm gốc 0. Ta có OA =
, cắt trục số tại điểm A nằm bên phải điểm gốc 0. Ta có OA = 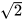 (điểm O biểu diễn điểm gốc 0) và A là điểm biểu diễn
(điểm O biểu diễn điểm gốc 0) và A là điểm biểu diễn 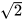 .
.
Nhận xét
• Do 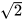 không phải là số hữu tỉ mà là số vô tỉ nên không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
không phải là số hữu tỉ mà là số vô tỉ nên không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
• Người ta chứng minh được rằng: Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
Vì thế, trục số còn được gọi là trục số thực (Hình 4).

Hình 4
III. SỐ ĐỐI CỦA MỘT SỐ THỰC
4 Đọc kĩ nội dung sau:
Gọi A là điểm (nằm bên phải điểm gốc 0) biểu diễn số thực 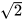 trên trục số nằm ngang.
trên trục số nằm ngang.
Gọi B là điểm nằm bên trái điểm gốc 0 sao cho OA = OB (điểm O biểu diễn điểm gốc 0). Khi đó, điểm B biểu diễn một số thực, kí hiệu là 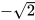 .
.
(Trang 40)
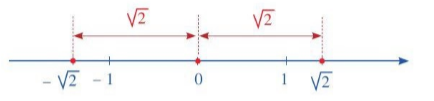
Hai điểm biểu diễn các số thực 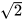 và
và 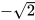 nằm về hai phía của điểm gốc () và cách đều điểm gốc 0.
nằm về hai phía của điểm gốc () và cách đều điểm gốc 0.
|
• Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau. • Số đối của số thực a kí hiệu là - a. • Số đối của số 0 là 0. |
Nhận xét: Số đối của số – a là số a, tức là – (a) = a.
Ví dụ 2. Tìm số đối của mỗi số sau: 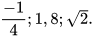
Giải
Số đối của 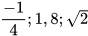 lần lượt là:
lần lượt là: 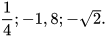
| 1. Tìm số đối của mỗi số sau:
|
IV. SO SÁNH CÁC SỐ THỰC
1. So sánh hai số thực
Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.
• Nếu số thực a nhỏ hơn số thực b thì ta viết a < b hay b > a.
• Số thực lớn hơn 0 gọi là số thực dương.
• Số thực nhỏ hơn 0 gọi là số thực âm.
• Số 0 không phải là số thực dương cũng không phải là số thực âm.
• Nếu a<b và b<c thì a<c.
2. Cách so sánh hai số thực
5
a) So sánh hai số thập phân sau: – 0,617 và – 0,614.
b) Nêu quy tắc so sánh hai số thập phân hữu hạn.
Trong những trường hợp thuận lợi, ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.
(Trang 41)
Ví dụ 3 So sánh:
a) 1,234567891011... và 1,234467891011...;
b) 0,3219199199919999... và 0,32(3).
Giải
a) Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn. Do 5 >4 nên 1,234567891011...> 1,234467891011... .
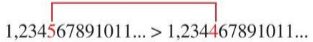
1,234567891011...> 1,234467891011...
b) Ta có 0,32(3) = 0,3233333... .
Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần nghìn. Do 1 <3 nên 0,3219199199919999...<0,32(3).

0,3219199199919999... <0,3233333...
| 2 So sánh hai số thực sau: a) 1,(375) và b) -1,(27) và -1,271. |
Chú ý: Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc sau: Với a, b là hai số thực dương, nếu a > b thì 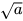 >
> 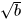 .
.
3. Minh hoạ trên trục số
Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta thừa nhận nhận xét sau:
– Nếu x< y hay y>x thì điểm x nằm bên trái điểm y;
– Ngược lại, nếu điểm x nằm bên trái điểm y thì x< y hay y>x.
Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng thừa nhận nhận xét sau:
– Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;
– Ngược lại, nếu điểm x nằm phía dưới điểm y thì x<y hay y>x.
Ví dụ 4
a) Sắp xếp các số sau theo thứ tự tăng dần: 3, − 1, 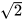 .
.
b) Trong ba điểm A, B, C trên trục số dưới đây có một điểm biểu diễn số thực 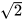 . Hãy xác định điểm đó.
. Hãy xác định điểm đó.

(Trang 42)
Giải
a) Ta có: – 1<0 và 0 < 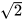 nên − 1 <
nên − 1 < 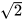 .
.
Do 2< 9 nên 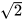 <
< 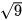 . Mà
. Mà 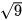 = 3 nên
= 3 nên 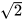 < 3.
< 3.
Vậy các số đã cho được sắp xếp theo thứ tự tăng dần là: – 1, 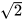 , 3.
, 3.
b) Do – 1< 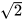 < 3 nên điểm
< 3 nên điểm 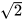 nằm bên phải điểm – 1 và nằm bên trái điểm 3 trên trục số nằm ngang. Trong ba điểm A, B, C, chỉ có điểm B thoả mãn hai điều kiện đó. Vậy điểm B biểu diễn số thực
nằm bên phải điểm – 1 và nằm bên trái điểm 3 trên trục số nằm ngang. Trong ba điểm A, B, C, chỉ có điểm B thoả mãn hai điều kiện đó. Vậy điểm B biểu diễn số thực 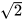 .
.
BÀI TẬP
1. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu a ∈ Z thì a ∈ R. b) Nếu a ∈ Q thì a ∈ R.
c) Nếu a ∈ R thì a ∈ Z. d) Nếu a ∈ R thì a ∈ Q.
2. Tìm số đối của mỗi số sau:
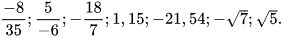
3. So sánh:
a) 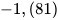 và
và 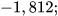 b)
b) 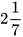 và
và 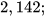
c) 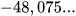 và
và 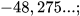 d)
d) 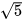 và
và 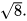
4. Tìm chữ số thích hợp cho  :
:
a) - 5,02 < -5,  1; b) - 3,7
1; b) - 3,7  8 > - 3,715;
8 > - 3,715;
c) - 0,5  (742) < - 0,59653; d) - 1,(4
(742) < - 0,59653; d) - 1,(4 ) < - 1,49.
) < - 1,49.
5. a) Sắp xếp các số sau theo thứ tự tăng dần:
- 2,63...; 3,(3); - 2,75...; 4,62.
b) Sắp xếp các số sau theo thứ tự giảm dần:
1,371...; 2,065; 2,056...;- 0,078...; 1,(37).
(Trang 43)
CÓ THỂ EM CHƯA BIẾT
Các phép tính với số thực
Trong tập hợp các số thực cũng có các phép tính (cộng, trừ, nhân, chia, luỹ thừa với số mũ tự nhiên) với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ.
1. Tính chất của phép cộng các số thực
• Giao hoán: a + b = b + a;
• Kết hợp: (a + b) + c = a + (b + c);
• Cộng với số 0: a + 0 = 0 + a = a;
• Cộng với số đối: a + (- a) = (- a) + a = 0.
(Ở đó a, b, c là các số thực)
2. Tính chất của phép nhân các số thực
• Giao hoán: a. b = b. a;
• Kết hợp: (a . b) . c = a . (b . c);
• Nhân với số 1: a.1 =1 . a = a;
• Phân phối đối với phép cộng: a . (b + c) = a .b+a.c;
• Với mỗi số thực a ≠ 0, có số nghịch đảo 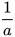 sao cho:
sao cho: 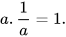
(Ở đó a, b, c là các số thực)
3. Phép tính luỹ thừa với số mũ tự nhiên của số thực
• Luỹ thừa với số mũ tự nhiên: 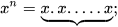 n thừa số x
n thừa số x
• Tích và thương của hai luỹ thừa cùng cơ số:
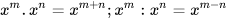 (x≠0, m≥n);
(x≠0, m≥n);
• Luỹ thừa của một luỹ thừa: 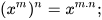
• Luỹ thừa của một tích, một thương:
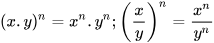 với y≠0.
với y≠0.
(Ở đó x, y là các số thực và m, n là các số tự nhiên)
4. Thứ tự thực hiện các phép tính, quy tắc chuyển vế, quy tắc dấu ngoặc trong tập hợp số thực cũng giống như trong tập hợp số hữu tỉ
Áp dụng. Tính:
a) 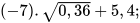 b)
b)