(Trang 32)
Trong chương này, chúng ta sẽ tìm hiểu những nội dung sau: số vô tỉ; căn bậc hai số học; tập hợp các số thực; giá trị tuyệt đối của một số thực; làm tròn và ước lượng; tỉ lệ thức, dãy tỉ số bằng nhau; đại lượng tỉ lệ thuận, đại lượng tỉ lệ nghịch và áp dụng vào bài toán thực tế.
Bài 1. SỐ VÔ TỈ.
CĂN BẬC HAI SỐ HỌC
Ngay từ thời xa xưa, phân số đã gắn bó với đời sống thực tiễn của con người trong suốt quá trình đo đạc, tính toán. Các nhà toán học Hy Lạp cổ đại thuộc trường phái Pythagoras còn cho rằng: “Tất cả các hiện tượng trong vũ trụ có thể được thu gọn thành các số nguyên và tỉ số của chúng”. Họ gọi các số nguyên và tỉ số của chúng là số rational, tức là những số có lí, mà ngày nay chúng ta quen gọi là số hữu tỉ. Tuy nhiên, vào thế kỉ V trước Công nguyên, nhà toán học Hippasus (530 – 450 trước Công nguyên) đã phát hiện ra rằng có những đối tượng trong thế giới tự nhiên không biểu thị được qua số hữu tỉ, chẳng hạn tỉ số giữa độ dài đường chéo hình vuông với cạnh của hình vuông đó thì không thể là số hữu tỉ. Phát minh của ông không được chấp nhận trong một thời gian dài, thậm chí những số như thế còn bị gọi là irrational, tức là những số vô lí hay không có lí.
(Nguồn: M.Kline, Mathematical Thought from Ancient to Modern Times, Vol.1, Oxford University Press, New York, 1990)
Trong bài học này, chúng ta sẽ làm quen với những số irrational như vậy, những số mà ngày nay chúng ta gọi là số vô tỉ.
I. SỐ VÔ TỈ
1. Khái niệm số vô tỉ
Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ, những số đó được gọi là số vô tỉ.
Ví dụ: Số Pi được người Babylon cổ đại phát hiện gần bốn nghìn năm trước và được biểu diễn bằng chữ cái Hy Lạp π từ giữa thế kỉ XVIII. Số π là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó. Năm 1760, nhà toán học Johann Heinrich Lambert (1728 – 1777, người Thụy Sĩ) đã chứng tỏ được rằng số π là số vô tỉ.
(Nguồn: M.Kline, Mathematical Thought from Ancient to Modern Times, Vol.1, Oxford University Press, New York, 1990)
(Trang 33)
2. Số thập phân vô hạn không tuần hoàn
1. Viết số hữu tỉ 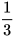 dưới dạng số thập phân vô hạn tuần hoàn.
dưới dạng số thập phân vô hạn tuần hoàn.
Số thập phân 0,333... = 0,(3) có vô số chữ số khác 0 ở phần thập phân của số đó. Những số thập phân như vậy gọi là số thập phân vô hạn. Tuy nhiên, có những số thập phân vô hạn mà ở phần thập phân của nó không có một chu kì nào cả, chẳng hạn, hai số 0,01001000100001000001... và – 5,02002000200002000002... Những số như vậy được gọi là số thập phân vô hạn không tuần hoàn.
Ví dụ: Dạng biểu diễn thập phân 3,1415926535897932384626433832795028841971... của số π là số thập phân vô hạn không tuần hoàn.
3. Biểu diễn thập phân của số vô tỉ
Cũng như số π, người ta chứng tỏ được rằng:
 Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn. Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn. |
Ví dụ 1 Các khẳng định sau đúng hay sai? Vì sao?
a) Nếu a ∈ Q thì a không thể là số vô tỉ.
b) Nếu a ∈ Z thì a không thể là số vô tỉ.
c) Số thập phân hữu hạn là số vô tỉ.
Giải
a) Đúng. Lí do như sau: Nếu a ∈ Q thì a là số hữu tỉ và do đó a được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn, tức là a không thể là số vô tỉ.
b) Đúng. Lí do như sau: Nếu a là số nguyên thì a cũng là số hữu tỉ và do đó theo lập luận ở trên a không thể là số vô tỉ.
c) Sai. Lí do như sau: Số thập phân hữu hạn không thể là số thập phân vô hạn không tuần hoàn và do đó không thể là số vô tỉ.
| 1 Khẳng định “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao? |
II. CĂN BẬC HAI SỐ HỌC
2 Tính: a) 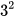 ; b)
; b) 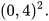
Số dương 3 thoả mãn 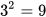 , ta gọi 3 là căn bậc hai số học của 9. Cũng như vậy, số dương 0,4 thoả mãn
, ta gọi 3 là căn bậc hai số học của 9. Cũng như vậy, số dương 0,4 thoả mãn 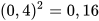 , ta gọi 0,4 là căn bậc hai số học của 0,16.
, ta gọi 0,4 là căn bậc hai số học của 0,16.
 Căn bậc hai số học của số a không âm là số x không âm sao cho Căn bậc hai số học của số a không âm là số x không âm sao cho 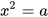 . . |
(Trang 34)
Chú ý
• Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là 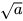 .
.
• Căn bậc hai số học của số 0 là số 0, viết là: 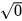 = 0.
= 0.
| Cho a ≥ 0, Khi đó:
|
Ví dụ 2 Chứng tỏ rằng:
a) Số 0,3 là căn bậc hai số học của số 0,09;
b) Số – 5 không phải là căn bậc hai số học của số 25.
Giải
a) Ta có 0,3 > 0 và  = 0,09 nên 0,3 là căn bậc hai số học của 0,09.
= 0,09 nên 0,3 là căn bậc hai số học của 0,09.
b) Tuy 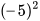 = 25 nhưng do − 5 < 0 nên – 5 không phải là căn bậc hai số học của số 25.
= 25 nhưng do − 5 < 0 nên – 5 không phải là căn bậc hai số học của số 25.
Ví dụ 3 Tìm giá trị của:
a) 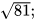 b)
b) 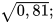 c)
c) 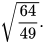
Giải. Ta có:
a) 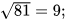 b)
b) 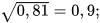 c)
c) 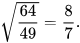
| 2. Tìm giá trị của: a) b) c) |
Nhận xét: Người ta chứng minh được rằng “Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì  là số vô tỉ”. Như vậy, các số
là số vô tỉ”. Như vậy, các số 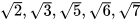 , ... đều là số vô tỉ.
, ... đều là số vô tỉ.
3. Ta có thể tính được giá trị ( đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn, để tính 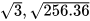 , ta sử dụng nút dấu căn bậc hai số học
, ta sử dụng nút dấu căn bậc hai số học  và làm như sau:
và làm như sau:
| Phép tính | Nút ấn | Kết quả |
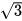 |  | 1, 7320508 |
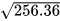 | 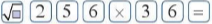 | 96 |
Ví dụ 4 Dùng máy tính cầm tay để tính giá trị (đúng hoặc gần đúng) trong mỗi trường hợp sau:
a) 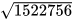 ; b)
; b) 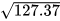 .
.
(Trang 35)
Giải. Thực hiện các bước như ở Hoạt động 3, ta có:
a) 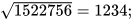 b)
b) 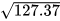 ≈ 68,5492524.
≈ 68,5492524.
BÀI TẬP
1. a) Đọc các số sau: 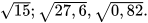
b) Viết các số sau: căn bậc hai số học của 39; căn bậc hai số học của 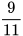 ; căn bậc hai số học của
; căn bậc hai số học của 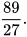
2. Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của số 0,64;
b) Số − 11 không phải là căn bậc hai số học của số 121;
c) Số 1,4 là căn bậc hai số học của 1,96 nhưng – 1,4 không phải là căn bậc hai số học của 1,96.
3. Tìm số thích hợp cho  :
:
| x | 144 | 1,69 |  |  |  | 2,25 | 0,025 |
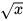 |  |  | 14 | 0,1 | 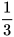 |  |  |
4. Tính giá trị của biểu thức:
a) 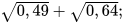 b)
b) 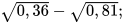
c) 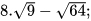 d)
d) 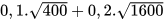
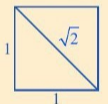
5. Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
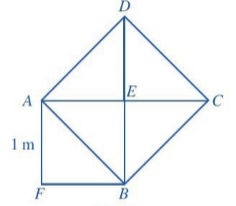
Hình 1
|
|
(Trang 36)
CÓ THỂ EM CHƯA BIẾT
Tỉ số vàng trong nghệ thuật và kiến trúc
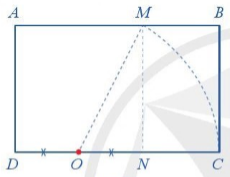
Tỉ số vàng là tỉ số chuẩn giữa các thành tố trong thiết kế nhằm đem lại hiệu ứng cao nhất cho con người khi thưởng thức các tác phẩm nghệ thuật. Những tỉ số đó thường là các số vô tỉ. Từ thời Hy Lạp cổ đại và Ai Cập cổ đại, người ta cho rằng hình chữ nhật vàng là hình chữ nhật
có tỉ số giữa chiều dài và chiều rộng là  (từ hình vuông AMND (Hình 2), gọi O là trung điểm của cạnh DN, vẽ đường tròn tâm O, bán kính OM; đường tròn này cắt đường thẳng DN ở C, dựng hình chữ nhật ABCD ta có một hình chữ nhật vàng).
(từ hình vuông AMND (Hình 2), gọi O là trung điểm của cạnh DN, vẽ đường tròn tâm O, bán kính OM; đường tròn này cắt đường thẳng DN ở C, dựng hình chữ nhật ABCD ta có một hình chữ nhật vàng).
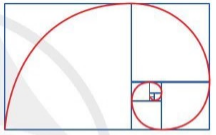
Đường xoắn ốc vàng là đường xoắn ốc tiếp xúc trong với các cạnh của một chuỗi các hình chữ nhật vàng (xem Hình 3).
|
Hình 2 |
Hình 3 |
Tỉ số vàng chi phối hầu hết các tác phẩm nghệ thuật, thiết kế đồ hoạ và kiến trúc nổi tiếng thế giới. Ví dụ, chúng ta có thể thấy đường xoắn ốc vàng trong bức chân dung nàng Mona Lisa của danh hoạ Leonardo da Vinci (1452 – 1519, người Ý), trong bức tranh “Thiếu nữ bên hoa huệ" của danh hoạ Tô Ngọc Vân (1906 – 1954, người Việt Nam) hay trong nhiều kiến trúc nổi tiếng thế giới như Đền thờ Parthenon ở Thủ đô Athens của Hy Lạp.
|
Bước chân dung nàng Mona Lisa |  |
(Trang 37)
|
Bức tranh “Thiếu nữ bên hoa huệ" |  |

Đền thờ Parthenon ở Thủ đô Athens của Hy Lạp
Tỉ số vàng và vũ trụTrong vũ trụ có rất nhiều dải ngân hà xoắn ốc theo đúng tỉ lệ của đường xoắn ốc vàng. Ví dụ dải ngân hà NGC 5 194 ở hình bên cách dải ngân hà của chúng ta khoảng 31 triệu năm ánh sáng (1 năm ánh sáng bằng khoảng 9,5 nghìn tỉ ki-lô-mét). (Nguồn: https://genk.vn/kham-pha/bi-an-ve-ti-le-vang- trong-moi-linh-vuc-20130603114924387.chn) |
Dải ngân hà NGC 5 194 |
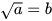 là đúng nếu: b ≥ 0 và
là đúng nếu: b ≥ 0 và 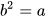 .
.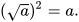
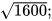
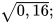
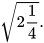
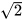 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1:
là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1: