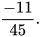(Trang 27)
Viết các số hữu tỉ 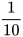 và
và 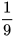 dưới dạng số thập phân ta được:
dưới dạng số thập phân ta được: 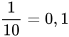 và
và 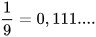
| Hai số thập phân 0,1 và 0,111... khác nhau như thế nào? Biểu diễn thập phân của số hữu tỉ như thế nào? |  |
I. SỐ THẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN
1 Đặt tính để tính thương: 33 : 20.
Ta đặt tính để tính thương 33 : 20 như sau:
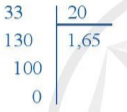
Nhận xét
• Số thập phân 1,65 chỉ có hai chữ số sau dấu “,”.
• Các số thập phân chỉ gồm hữu hạn chữ số sau dấu “,” được gọi là số thập phân hữu hạn.
Ví dụ 1 Sử dụng máy tính cầm tay để viết thương của phép chia 51 : 125 dưới dạng số thập phân hữu hạn.
Giải
Ta có: 51 : 125 = 0,408. Đó là số thập phân hữu hạn.
2 Đặt tính để tính thương: 4 : 3.
Ta đặt tính để tính thương 4 : 3 như sau:
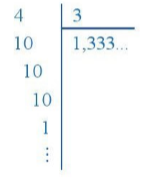
(Trang 28)
Nhận xét: Phép chia này không bao giờ chấm dứt. Nếu cứ tiếp tục chia thì trong phần thập phân của thương, chữ số 3 sẽ xuất hiện liên tiếp mãi. Ta nói rằng khi chia 4 cho 3, ta được số 1,333..., đó là số thập phân vô hạn tuần hoàn.
Ví dụ 2 Sử dụng máy tính cầm tay để thực hiện mỗi phép chia sau:
a) 7:30; b) 1 219: 9900.
Giải
a) 7:30=0,2333....
b) 1 219: 9900=0,12313131....
| 1. Sử dụng máy tính cầm tay để viết thương của mỗi phép chia sau dưới dạng số thập phân vô hạn tuần hoàn: a) |
Nhận xét: Các số thập phân vô hạn tuần hoàn 1,333...; 0,2333...; 0,12313131... đã nêu ở trên có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi. Cụ thể:
• Trong phần thập phân của số 1,333..., chữ số 3 xuất hiện liên tiếp mãi ngay từ hàng phần mười. Số 3 gọi là chu kì của số thập phân vô hạn tuần hoàn 1,333... và số thập phân đó được viết gọn là 1,(3), tức là:
4 : 3 = 1,333... = 1,(3).
• Trong phần thập phân của số 0,2333..., chữ số 3 xuất hiện liên tiếp mãi bắt đầu từ hàng phần trăm. Số 3 cũng là chu kì của số thập phân vô hạn tuần hoàn 0,2333... và số thập phân đó được viết gọn là 0,2(3), tức là:
7 : 30 = 0.2333... = 0.2(3).
• Trong phần thập phân của số 0,12313131..., cụm chữ số liền nhau 31 xuất hiện liên tiếp mãi bắt đầu từ hàng phần nghìn. Số 31 cũng là chu kì của số thập phân vô hạn tuần hoàn 0,12313131... và số thập phân đó được viết gọn là 0,12(31), tức là:
1 219 : 9 900 = 0,12313131... = 0,12(31).
II. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Ta đã biết mỗi số hữu tỉ đều viết được dưới dạng phân số 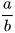 với a, b ∈ Z; b>0. Thực hiện phép tính a : b, ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
với a, b ∈ Z; b>0. Thực hiện phép tính a : b, ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Nhận xét: Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.
(Trang 29)
BÀI TẬP
1. Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: 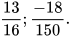
2. Viết mỗi phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kì): 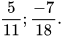
3. Viết mỗi số thập phân hữu hạn sau dưới dạng phân số tối giản:
a) 6,5; b) - 1,28; c) - 0,124.
4. Sử dụng máy tính cầm tay để thực hiện mỗi phép chia sau:
a) 1 : 99; b) 1 : 999; c) 8,5 : 3; d) 14,2 : 3,3.
TÌM TÒI – MỞ RỘNG
Dạng biểu diễn thập phân của số hữu tỉ
Ta đã biết mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Vấn đề đặt ra là biểu diễn thập phân của số hữu tỉ khi nào là số thập phân hữu hạn? Khi nào là số thập phân vô hạn tuần hoàn?
Giả sử số hữu tỉ r viết được dưới dạng phân số tối giản 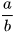 (a, b ∈ Z; b > 0).
(a, b ∈ Z; b > 0).
Người ta đã chứng minh được định lí sau:
• Các phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì viết được dưới dạng số thập phân hữu hạn và chỉ những phân số đó mới viết được dưới dạng số thập phân hữu hạn.
• Các phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì viết được dưới dạng số thập phân vô hạn tuần hoàn và chỉ những phân số đó mới viết được dưới dạng số thập phân vô hạn tuần hoàn.
Từ định lí trên, ta có sơ đồ phân loại biểu diễn thập phân của số hữu tỉ như sau:
Biểu diễn thập phân của số hữu tỉ 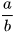 (a, b ∈ Z; b > 0; 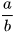 là phân số tối giản) là phân số tối giản) | |
| Biểu diễn bằng số thập phân hữu hạn | Biểu diễn bằng số thập vô hạn tuần hoàn |
| Mẫu b không có ước nguyên tố khác 2 và 5 | Mẫu b có ước nguyên tố khác 2 và 5 |
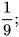 b)
b)