(Trang 87)
Ví dụ 1
Tìm độ dài x trong Hình 4.27.
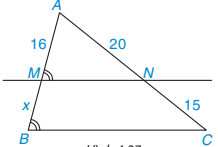
Hình 4.27
Giải. (H.4.27)
Ta có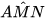 
= 
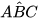(giả thiết), mà hai góc này ở vị trí đồng vị nên MN // BC (dấu hiệu nhận biết hai đường thẳng song song).
Suy ra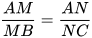 
(định lí Thalès trong tam giác) hay 
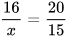, suy ra 
.
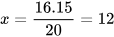Ví dụ 2
Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB tại D, tia phân giác của góc AMC cắt cạnh AC tại E. Chứng minh DE II BC.
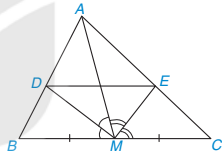
Hình 4.28
Giải. (H.4.28)
Trong △AMB, MD là phân giác của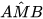 
nên
(tính chất đường phân giác trong tam giác). (1)
Trong △AMC, ME là phân giác của AMC nên
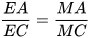(tính chất đường phân giác trong tam giác). (2)
Mặt khác, MB = MC (do M là trung điểm của BC). (3)
Từ (1), (2) và (3) suy ra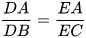 
.
Do đó DE II BC (định lí Thalès đảo).
Ví dụ 3
Cho △ABC vuông tại A, đường cao AH (H = BC). Gọi I và K lần lượt là trung điểm của AH và HB.
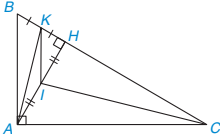
Hình 4.29
Chứng minh rằng:
a) IK ⊥ AC; b) AK ⊥ Cl.
Giải (H.4.29)
a) Tam giác AHB có I là trung điểm của AH, K là trung điểm của BH nên KI là đường trung bình của △AHB.
(Trang 88)
Từ đó, suy ra KI II AB (tính chất đường trung bình của tam giác).
Vì AB ⊥ AC (do △ABC vuông tại A) nên KI ⊥ AC.
b) Tam giác AKC có: AH ⊥ KC (giả thiết);
KI ⊥ AC (chứng minh trên).
Vì AH cắt KI tại I nên I là trực tâm của △AKC. Suy ra CI ⊥ AK.
BÀI TẬP
4.13. Tìm độ dài x trong Hình 4.30
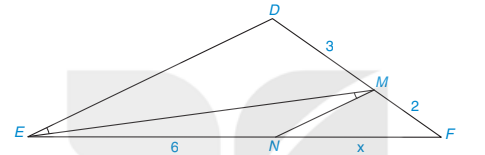
Hình 4.30
4.14. Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK II CD, FK II AB.
b) So sánh EF và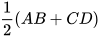 
.
4.15. Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng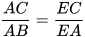 
.
4.16. Tam giác ABC có AB= 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.
a) Tính độ dài đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
4.17. Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: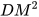 
= MN . MK.
