(Trang 76)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Tỉ số hai đoạn thẳng - Đoạn thẳng tỉ lệ | - Định lí Thalès trong tam giác (thuận và đảo). - Tính độ dài đoạn thẳng bằng cách sử dụng định lí Thalès. - Giải quyết một số vấn đề thực tiễn gắn với việc vận dụng định lí Thalès. |
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
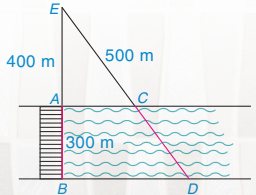
Hình 4.1
(Trang 77)
1 ĐOẠN THẲNG TỈ LỆ
Tỉ số của hai đoạn thẳng
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:

Hình 4.2
HĐ1 Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số 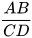 .
.
HĐ2 Dùng thước thẳng, đo độ dài hai đoạn AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số 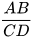 .
.
HĐ3 So sánh hai tỉ số tìm được trong hai hoạt động trên.
Ta có nhận xét rằng: Khi ta thay đổi đơn vị đo, tỉ số độ dài của hai đoạn thẳng AB và CD không thay đổi. Ta gọi tỉ số đó là tỉ số của hai đoạn thẳng AB và CD.
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Luyện tập 1 Tìm tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) MN = 3 cm và PQ = 9 cm. b) EF = 25 cm và HK = 10m.
Đoạn thẳng tỉ lệ
Cho bốn đoạn thẳng AB, CD, A'B', C'D' (H.4.3). Ta thấy
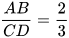 ;
; 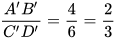 . Ta có tỉ lệ thức
. Ta có tỉ lệ thức 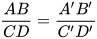 .
.
Khi đó, ta nói AB và CD tỉ lệ với A'B' và C'D'.
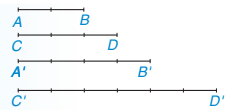
Hình 4.3
Ta có định nghĩa sau:
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B'và C'D' nếu có tỉ lệ thức:
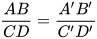 hay
hay 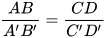 .
.
(Trang 78)
Luyện tập 2
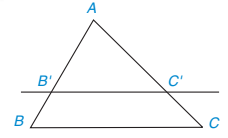
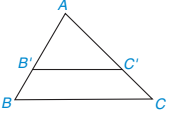
Cho tam giác ABC và một điểm B' nằm trên cạnh AB. Qua điểm B', ta vẽ một đường thẳng song song với BC, cắt AC tại C' (H.4.4). Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:
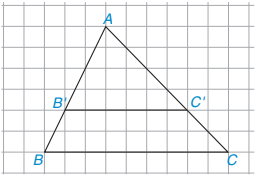
Hình 4.4
a) 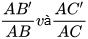 ;
;
b) 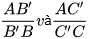 ;
;
c) 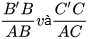
2 Định lí Thalès trong tam giác
Định lí Thalès trong tam giác
Trong Luyện tập 2, khi B'C' song song với BC, ta có các tỉ lệ thức:
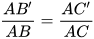 ;
; 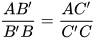 ;
; 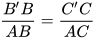
Một cách tổng quát, ta có định lí sau:
Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
| GT | △ABC, B'C' // BC (B'∈AB; C'∈AC) |
| KL |
|
Ví dụ 1 Tính độ dài x trong Hình 4.5(*), biết MN // EF.
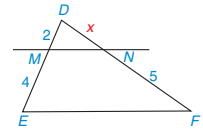
Hình 4.5
Giải
Xét tam giác DEF có MN II EF nên theo định lí Thalès, ta có:
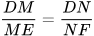 hay
hay 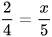 , suy ra
, suy ra 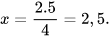
(*) Các số chỉ kích thước trên mỗi hình có cùng đơn vị đo.
(Trang 79)
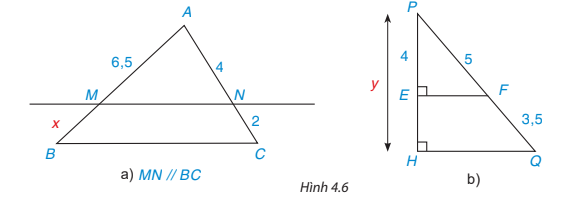
Luyện tập 3 Tìm các độ dài x, y trong Hình 4.6.
Định lí Thalès đảo
HĐ4 Cho △ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 4 cm, AC' = 6 cm (H.4.7).
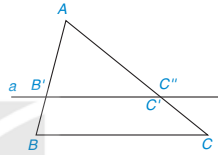
Hình 4.7
• So sánh các tỉ số 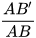 và
và 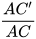 .
.
• Vẽ đường thẳng a đi qua B' và song song với BC, đường thẳng a cắt AC tại điểm C". Tính độ dài đoạn thẳng AC".
• Nhận xét gì về hai điểm C', C" và hai đường thẳng B'C', BC?
Ta thừa nhận định lí sau:
Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
| HT | △ABC, B'∈AB; C'∈AC; 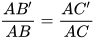 |
| KL | B'C' //BC |
Ví dụ 2
Quan sát Hình 4.8. Chứng minh rằng MN // EF.
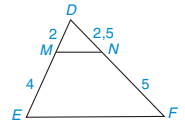
Hình 4.8
Trong △DEF, ta có: 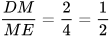 ;
; 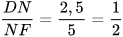 .
.
Vì 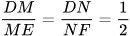 nên MN // EF (định lí Thalès đảo)
nên MN // EF (định lí Thalès đảo)
(Trang 80)
Vận dụng
Em hãy trả lời câu hỏi trong tình huống mở đầu.
BÀI TẬP
4.1. Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).
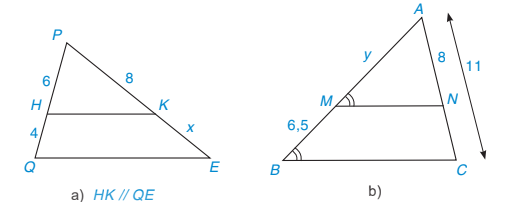
Hình 4.9
4.2. Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích vì sao chúng song song với nhau.
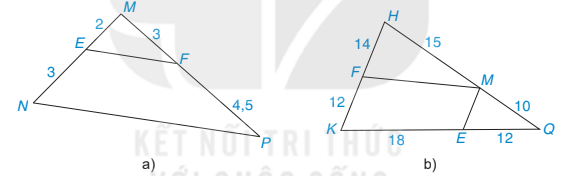
Hình 4.10
4.3. Cho △ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh rằng: 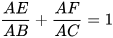
4.4. Cho △ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng 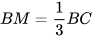 .
.
4.5. Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H. 4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
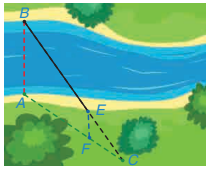
Hình 4.11