(Trang 46)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
|
|
Để kiểm tra các thanh ngang trên mái nhà đã song song với nhau chưa, người thợ chỉ cần kiểm tra chúng có cùng vuông góc với một thanh dọc. Vì sao lại như vậy, chúng ta cùng tìm hiểu qua bài học này.
1) CÁC GÓC TẠO BỞI MỘT ĐƯỜNG THẲNG CẮT HAI ĐƯỜNG THẲNG
Góc so le trong, góc đồng vị
Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A, bốn góc đỉnh B được đánh số như hình 3.16. Ta sắp xếp các góc thành từng cặp. Mỗi cặp gồm một góc đỉnh A và một góc đỉnh B.
- Các cặp góc
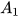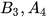và 
và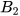 
được gọi là các góc so le trong. - Các cặp góc
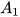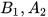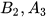và 
và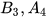 
và 
và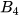 
được gọi là các cặp góc đồng vị.
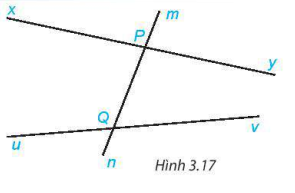
Cho đường thẳng mn cắt hai đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17). Em hãy kể tên:
a) Hai cặp góc so le trong;
b) Bốn cặp góc đồng vị.
(Trang 47)
Quan hệ giữa các cặp góc so le trong, cặp góc đồng vị
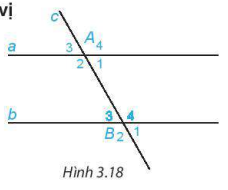
Trên hình 3.18, cho biết hai góc so le trong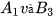 
bằng nhau vàng bằng 60°.
HĐ1 Hãy tính và so sánh hai góc so le trong còn lại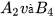 
.
HĐ2 Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Ta có tính chất sau:
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
- Hai góc so le trong còn lại bằng nhau;
- Hai góc đồng vị bằng nhau.
Luyện tập 1
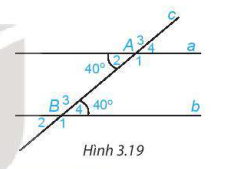
Quan sát hình 3.19.
a) Biết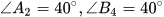 
. Em hãy tính số đo các góc còn lại.
b) Các cặp góc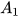 
và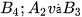 
được gọi là các cặp góc trong cùng phía. Tính các tổng: 
.
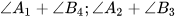2) DẤU HIỆU NHẬN BIẾT HAI ĐƯỜNG THẲNG SONG SONG
Để biết hai đường thẳng cắt nhau hay song song với nhau, ta cần biết chúng có điểm chung hay không. Việc kiểm tra trực tiếp, tức là xác định điểm chung của hai đường thẳng đã cho, trong nhiều trường hợp, là rất khó thực hiện. Chẳng hạn trên hình 3.20a, không phải lúc nào ta cũng có thể kéo dài được hai đường thẳng c và d để tìm điểm chung của chúng. Vậy có cách nào thuận tiện hơn để nhận biết hai đường thẳng song song hay không?
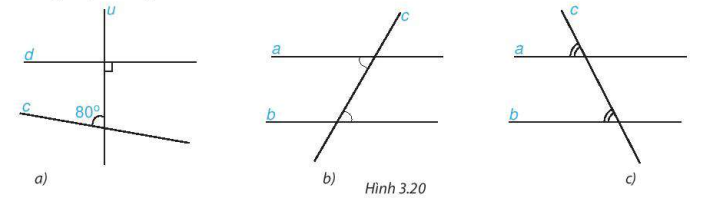
Ta thừa nhận rằng:
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau (H.3.20b,c).
(Trang 48)
Ví dụ
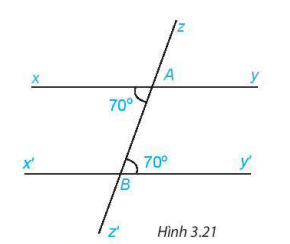
Quan sát hình 3.21 và giải thích tại sao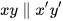 
.
Giải
Ta có ∠xAB = ∠ABy' = 70°.
Hai góc này ở vị trí so le trong. Do đó 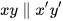(dấu hiệu nhận biết hai đường thẳng song song).
Luyện tập 2
- Quan sát hình 3.22 và giải thích vì sao
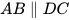. - Tìm trên hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song.
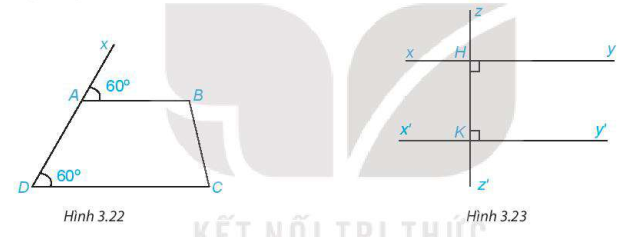
Nhận xét. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Thực hành 1
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn 60° của êke để vẽ như sau:
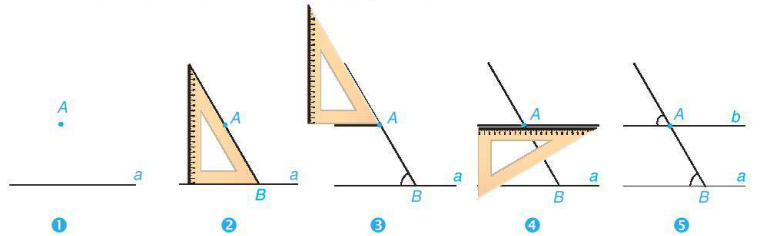
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau?
(Trang 49)
Thực hành 2
Dùng góc vuông hay góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua A và song song với đường thẳng a cho trước.
BÀI TẬP
3.6. Quan sát hình 3.24.
- Tìm một góc ở vị trí so le trong với góc MNB.
- Tìm một góc ở vị trí đồng vị với góc ACB.
- Kể tên một cặp góc trong cùng phía.
- Biết
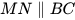, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ.
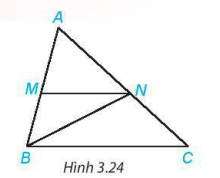
3.7. Quan sát hình 3.25. Biết ∠MEF = 40°, ∠EMN = 40°. Em hãy giải thích tại sao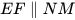 
.
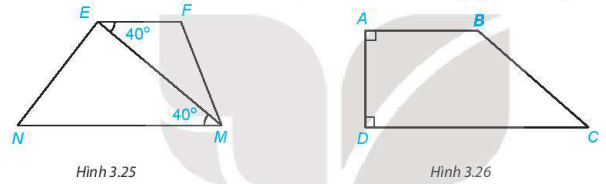
3.8. Quan sát hình 3.26, giải thích tại sao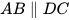 
.
3.9. Cho điểm A và đường thẳng d không đi qua A. Hãy vẽ đường thẳng d' đi qua A và song song với d.
3.10. Cho hai điểm A và B. Hãy vẽ đường thẳng a đi qua A và đường thẳng b đi qua B sao cho a song song với b.
3.11. Hãy vẽ hai đường thẳng AB và MN sao cho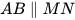 
và AB = MN.
